Contexto

Hace algunas semanas realicé el análisis de una construcción cuya fotografía dejo a continuación:

En la fotografía lo que más salta a la vista son las dos columnas de esquina que a través de una losa de transferencia se transfieren su carga a una columna central en planta baja. En el vídeo del análisis salió a consideración la idea de además hacer un análisis de la losa en voladizo al fondo de la fotografía.

Como para el análisis de la losa de transferencia necesitaba medidas aproximadas, realicé otro video tutorial de como medir distancias a partir de una fotografía. Los enlaces a los dos videos mencionados los dejo a continuación:
VÍDEO: Columna truncada en planta baja
VÍDEO: Cómo obtener distancias desde una fotografía

Saltó a la vista la distancia de voladizo de 2.30m que se puede ver en la imagen. Entonces decidí hacer una revisión del voladizo mostrado.

Explicación en vídeo

Si prefieres consumir contenido multimedia con la revisión de este caso, puedes verlo en el siguiente vídeo:

Planteamiento del problema

La losa mostrada en la imagen al fondo, vuela a partir de una fila de columnas sin vigas. La losa es maciza y a partir de las medidas realizadas, tiene una longitud de 2.30m aproximadamente y una altura que casi con toda certeza es de 20cm de espesor.

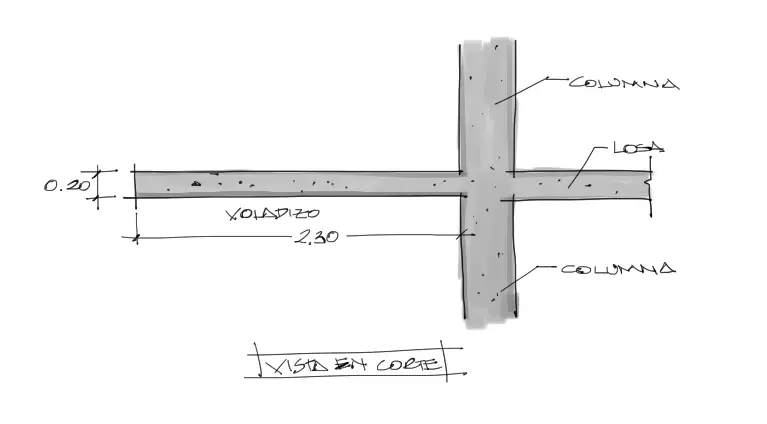
Para la revisión del voladizo asumiremos resistencias de concreto y acero típicas. O sea: fc’=20MPa y fy=410MPa.

Cargas

Se debe realizar una estimación de cargas en base al uso de los ambientes, que en el caso más típico serán viviendas. Por tanto planteamos los siguientes terminados sobre la losa:

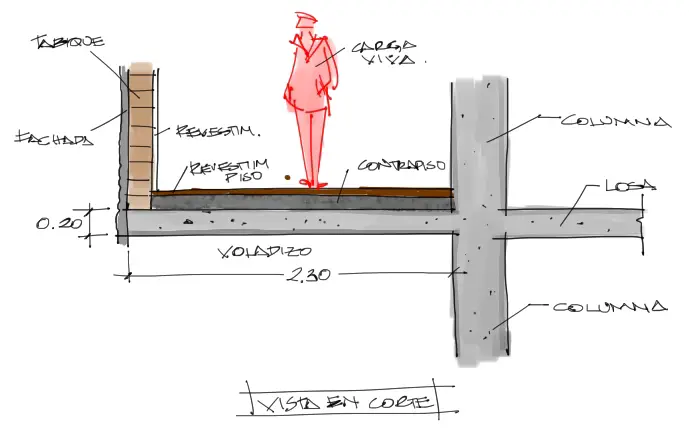
Las cargas mínimas necesarias a colocarse sobre el voladizo son, en orden: un tabique hacia la fachada, un contrapiso nivelador de unos 5cm de espesor, un revestimiento de cerámica o parquet, y finalmente la carga de uso.

Todas estas cargas deben traducirse en cargas lineales sobre el voladizo.

La carga de tabique se convierte en una carga puntual aplicada en el borde del voladizo. Si la carga por m2 de tabique con revestimientos es de 2.1KN/m2 y la altura del tabique a levantar es de 2.8m, entonces la carga total que llega al borde del voladizo producto del tabique es de 2.1KN/m2*2.8m*1m (1m de profundidad).

La carga de contrapiso más revestimiento más revoque de cielo se calcula con el peso específico del concreto de 24 KN/m3 que al multiplicar por el espesor de la losa de 0.05m, revestimiento de 0.01m y por la profundidad de 1m se tiene la carga linealizada por contrapiso y revestimiento. O sea: 24KN/m3*(0.05+0.01) = 1.44kN/m. Se adopta 1.5KN/m para considerar el revoque de cielo raso en la parte inferior de la losa.

El peso propio de la losa se calcula de manera similar. Es el espesor de la losa de 0.20m por el peso específico del hormigón y por un metro de profundidad: PesoPropio = 24KN/m3*0.20m*1m = 4.80kN/m

Solicitaciones

Las solicitaciones de momento flector y de cortante en el voladizo se obtienen para realizar un análisis de resistencias. Y para este tipo de análisis se deben mayorar las cargas por un factor de 1.2 y las cargas vivas por un factor de 1.6. Realizando esta multiplicación sobre las cargas del ejercicio se tiene:

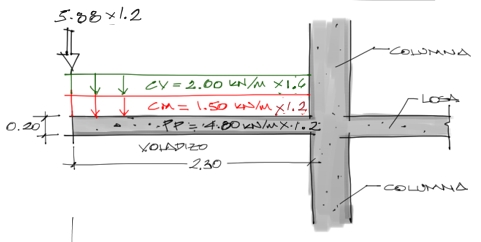
Y para estas cargas podemos ya obtener las solicitaciones del voladizo. El capítulo de “SOLICITACIONES INTERNAS EN VIGAS ISOSTÁTICASte ayudará a entender como obtener estas solicitaciones en caso de que tengas problemas con ello.

Los diagramas de cortante y momento flector a partir de las cargas factorizadas serán entonces:

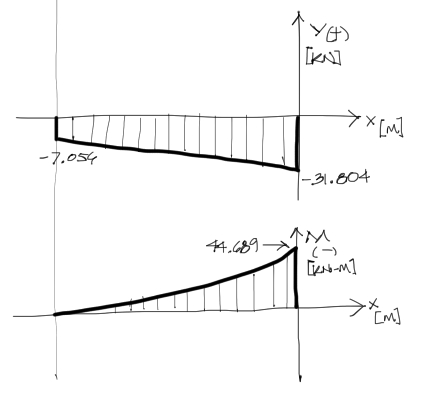
Con estas solicitaciones deberemos a continuación realizar un análisis de resistencias del voladizo

Diseño a flexión

Si bien este es un problema de revisión del diseño del voladizo, nosotros no conocemos el acero que existe dentro de la estructura existente. Por tanto debermos nosotros obtener esa cantidad de acero y de modo cualitativo estimar si la cantidad de acero que obtenemos del análisis es razonable con parámetros reales constructivos. En otras palabras, veremos si el acero que obtenemos está en rangos aceptables.

Toda la teoría de diseño de flexión de una losa es un tanto extenso, sin embargo la teoría de flexión en videos y texto la encuentas en los enlaces siguientes:
Diseño de vigas a flexión sin acero a compresión
Diagrama de flujo de diseño de losas a flexión
… y en general todo el capítulo de DISEÑO A FLEXIÓN y de LOSAS dentro de la TABLA DE CONTENIDO DE HORMIGÓN ARMADO de mi página web.

Sin embargo podemos simplemente introducir los parámetros en el Programa de diseño a flexión de losas de hormigón y obtenemos lo siguiente:

El acero necesario para resistir el momento de 44.689KNm es de 7.53cm2 que debemos convertir a barras de acero. Así mismo en la dirección perpendicular se debe colocar acero mínimo por retracción y fraguado que es de 3.69cm2. Ambos traducidos en cantidad de barras representa fierro de 12mm cada 15cm y fierro de 10mm cada 20cm respectivamente.

En Este Enlace puedes averiguar cuantos cm2 tiene cada diámetro de barra para llegar al refuerzo mostrado en la imagen arriba.

Diseño a cortante

Uno de los motivos por los cuales se comenzó por el diseño a flexión antes que por la revisión de resistencia de cortante, es porque según la nueva norma ACI318-19, se necesita conocer la cantidad de acero longitudinal del elemento a flexión (As=7.53cm2) para poder conocer la resistencia a cortante del elemento.

Toda la teoría de diseño a cortante es bastante extensa, sin embargo se reduce a una sola fórmula para la resistencia de losas:

En la fórmula mostrada:
Vc = Resistencia nominal del hormigón en la losa en voladizo
λs = factor de altura. toma valor de 1 para alturas de 250mm o menos (nuestro caso de análsis)
λ = Factor de hormigón liviano. Valor de 1 para densidades normales y 0.7 para hormigón liviano
ρw = cuantía de acero lontigudinal a tracción en la viga = As/(b·d)
fc’ = resistencia característica del hormigón (en MPa)
bw = ancho del elemento de análisis
d = Altura efectiva medida desde la cara comprimida hasta el eje de los aceros a tracción.

En nuestro caso, λs=1, λs=1, fc’= 20MPa, bw=1m, d=0.17m

La cuantía longitudinal debe calcularse en las mismas unidades para el numerador como para el denominador, entonces convertimos los 7.53cm2 a m2. Además la distancia “d” se mide desde la cara inferior del voladizo (que es la cara comprimida) al eje de los aceros a tracción. Si 0.20m es la altura total del voladizo, quitando recubrimientos de 3cm de hormigón, la distancia d=0.17m. Entonces: ρw=7.53e-4/(1*0.17)=4.43e-3

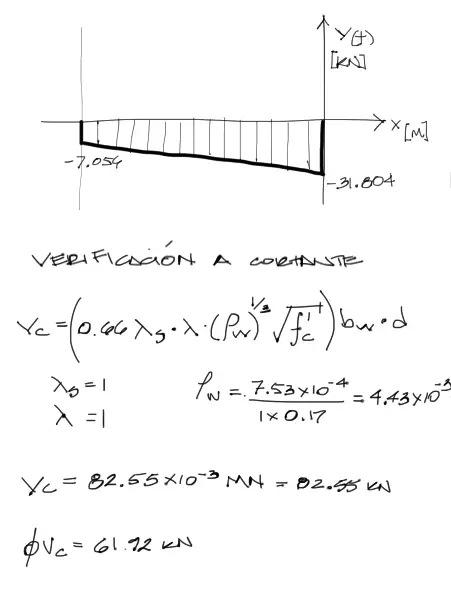
Hecho el cálculo se obtiene una resistencia nominal del concreto igual a 82.55e-3 [MN] (el resultado se obtiene en MN pues el ingreso de datos se hizo en MPa y en m). convirtiendo esta expresión a KN se tiene una resistencia de 82.55KN. Esta resistencia tiene que reducirse por un factor de seguridad ø=0.75 segun la ACI. Por tanto la resistencia de diseño de la sección de concreto del voladizo es de 61.92 KN

Esta resistencia debe compararse con la solicitación de cortante más crítica que es de 31.804KN. Como las resistencias son mayores a las solicitaciones, la losa aguanta las cargas de diseño.

Verificación de deflexiones

¿Cuándo calcular deflexiones?

La norma ACI318-19 indica en diferentes capítulos, las dimensiones mínimas que debe tener un elemento estructural, para que bajo cargas convencionales, trabaje de manera adecuada. Si se violan estas directrices y se construyen elementos más esbeltos que lo sugerido por la norma, la misma indica que se deben hacer verificaciones de deflexión en el elemento.

Para el caso de losas, éstas deben tener un peralte mínimo en función a la luz, según el siguiente detalle:

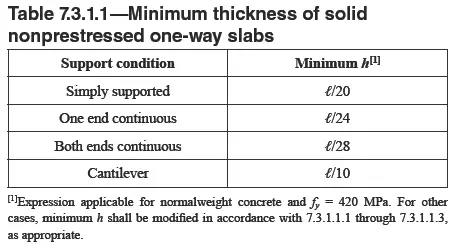
La tabla indica que para el caso de voladizos, la altura mínima de losa deberá ser L/10. En nuestro caso 2.30m/10 = 0.23m. La losa del ejemplo tiene solo 0.20m o 20cm por lo que es obligatorio un análisis de deflexiones.

Deflexión admisible

Las deflexiones que se calculen en el voladizo, deberán compararse con las deflexiones admisibles máximas que estipula la norma. En resumen se debe aplicar esta tabla:

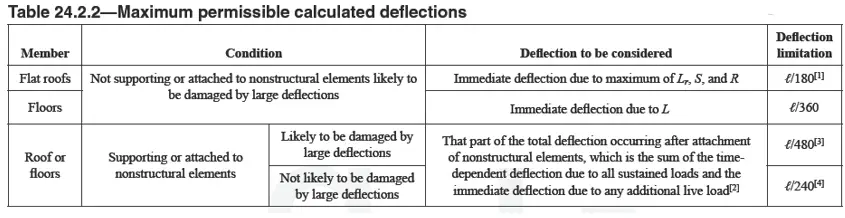
La tabla entera la explico a todo detalle en el artículo Deflexiones admisibles en vigas y losas. En resumen, cuando se tienen elementos frágiles sostenidos por la viga o losa (en este caso el tabique de cerámica es un material frágil), el caso que nos compete es el de Δmax = L/480.

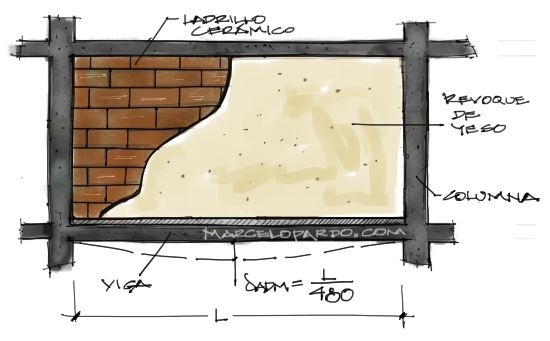
O sea que para nuestro análisis, si el voladizo tiene 2.30m de longitud, Δmax = 2.30/480 = 0.0048m o 4.8mm. Eso quiere decir que la deflexión real de la losa de análisis debe ser como máximo de 4.8mm. Ahora nos tocará calcular esta deflexión real y ver si es menor o igual a los 4.8mm permitidos por la norma.

Deflexiones reales – Inercia fisurada de la viga

El cálculo de deflexiones reales de un elemento estructural tiene un proceso más o menos largo, y es por eso que se busca evitarlo obedeciendo las directrices de la tabla 7.3.1.1.

Para el cálculo de la deflexión debemos tomar en consideración el cálculo de deflexiones inmediatas y el cálculo de deflexiones diferidas en el tiempo.

Para ambos tipos de deflexión se debe calcular previamente la inercia efectiva de la sección transversal de la losa a partir de la siguiente fórmula:

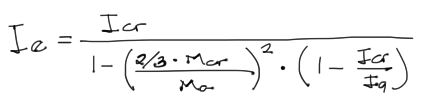
donde:
Ie = Inercia efectiva (parcialmente fisurada) de la losa
Icr = Inercia fisurada de la losa = 0.25Ig
Ig = Inercia bruta de la losa = b·h³/12
Ma = Momento flector máximo solicitante en estado límite de servicio
Mcr = Momento flector para el cual se produce la fractura del concreto en la zona traccionada

A la vez, el momento Mcr se calcula a partir de:

De todos estos parámetros:
fr = Esfuerzo de fractura del concreto a tracción
Yt = distancia desde el eje neutro a la fibra traccionada de la losa
A partir del reemplazo de todas las variables en la fórmula de Mcr se obtiene un valor de momento al cual se produce la fractura de la viga de 18.5 KN-m. Si el momento solicitante en servicio es mayor a 2/3Mcr, entonces la viga tendrá grietas de tracción que reducirán la inercia bruta de la viga y deberá calcularse “Ie”. Si el momento solicitante en servicio Ma no fuera mayor a 2/3Mcr, entonces se puede usar la inercia bruta “Ig” en el análisis de deflexiones.

En nuestro caso el momento solicitante Ma se calcula a partir de las cargas sin mayorar:

El cálculo arriba consiste en el simple equilibrio de la reacción de momento flector en el apoyo del voladizo equilibrando cargas externas con el momento en el empotramiento.

Se puede apreciar que el momento Ma es mucho más grande que Mcr y claro está, más grande que 2/3·Mcr. Por tanto deberemos trabajar con la inercia efectiva Ie en el cálculo de deflexiones. Calculamos Ie en función a los parámetros ya calculados:

Esta inercia será la que utilicemos en el cálculo de deflexiones del voladizo tanto para cargas puntuales como para cargas distribuidas.

Deflexiones reales – Fórmulas de deflexión de voladizos

La deflexión de un voladizo en general es sencilla de calcular. Su cálculo está en función de teoría de resistencia de materiales. A continuación te dejo el enlace a la manera de calcular deflexiones en volados:
Demostración de deflexión de voladizo para carga distribuida
Demostración de deflexión de voladizo para carga puntual

En concreto, lo que necesitamos es la fórmula de deflexión para ambas situaciones de carga, y son las siguienets:

Deflexiones reales del voladizo – Inmediata y Diferida

A partir de las fórmulas de deflexión de un voladizo ya podemos calcular las deflexiones del volado. Para eso necesitamos el módulo elástico(E), la inercia (Ie), las cargas distribuidas y puntual (P y q). Todos son datos excepto el módulo elástico, que según la ACI se calcula a partir de la fórmula:

En la fórmula mostrada, la resistencia fc’ debe introducirse en MPa. A partir de ese cálculo ya podemos conocer la rigidez del voladizo multiplicando E por Ie calculado anteriormente.

Volviendo a la tabla 24.2.2 de deflexiones admisibles, la tabla indica que para el cálculo de las deflexiones reales se deben considerar las deformaciones instantaneas colocadas luego del elemento frágil más todas las cargas diferidas muertas. Además se deben adicionar las deflexiones por cargas vivas instantaneas.

Deflexiones instantaneas

Las deflexiones instantaneas vivas y muertas se calculan fácilmente a partir de las fórmulas de deflexión de voladizo. Las deflexiones a considerar son:
– Deflexión por carga de tabique
– Deflexión por carga de contrapiso
– Deflexión por carga viva

Haciendo los cálculos numéricos se tiene entonces:

Deflexiones diferidas en el tiempo

Para entender como calcular las deflexiones a lo largo del tiempo, debemos explicar esta gráfica:

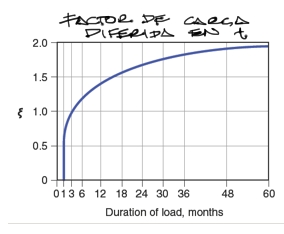
La gráfica muestra un factor ξ que crece en función de los meses. ξ representa cuantas veces más se deformará un elemento estructural en el tiempo en relación a las deformaciones instantáneas. O sea que si una viga se deforma instantáneamente 8mm, la misma viga a lo largo del de 3 meses sufrirá una deflexión adicional de 8mm (ξ=1) y a lo largo de 60 meses sufrirá una deflexión diferida en el tiempo de 16mm (ξ=2), sumando un total de 24mm al cabo de los 60 meses.

Como la mayoría de las cargas muertas son permanentes, se supone que para todos los casos aplicaremos ξ=2 de las cargas diferidas en el tiempo. En este caso se deben calcular además las deflexiones diferidas en el tiempo del peso propio de la losa del voladizo, pues esta deformación se genera DESPUÉS de la construcción del tabique. Sin embargo para este último caso ξ será solo igual a 1 ya que desde la construcción del voladizo hasta la construcción del tabique ya pasaron en promedio 3 meses, por tanto se considera el ξ desde esos 3 meses hasta los 60 meses.

Calculando entonces:

Deflexiones totales

La suma de la deflexión total real del voladizo es la simple suma de las deflexiones instantáneas y las diferidas en el tiempo, teniendo un total de:

Se puede concluir que el voladizo se deformará con el tiempo mucho más que la deflexión permitida por norma. Es así que este voladizo no debería construirse. Si se quisiera construir un voladizo de esta dimensión debería incrementarse la altura de la losa o rigidizar el volado mediante vigas peraltadas que conviertan a la losa en una losa apoyada en 3 bordes (viga entre columnas y dos vigas en voladizo). Las soluciones son diversas, sin embargo tal cual se ve en la foto del inicio del artículo, este voladizo tiene grandes probabilidades de deformarse más de lo permitido, y generar por tanto fisuras que preocuparán a los que habiten el inmueble.

Conclusiones

Muchas estructuras son resistentes a las cargas impuestas, sin embargo se deforman demasiado. Tal es el caso del presente análisis, donde si bien el voladizo no colapsará nunca, éste estará sujeto a deformaciones tan grandes que probablemente fisuren la fachada y revoques internos, además de generar preocupación en sus habitantes.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO ←←←

←←← VOLVER A TABLA DE CONTENIDO DE CONSTRUCCIÓN ←←←