Enunciado

Resolver las deflexiones en el extremo derecho y al centro de la viga mostrada:

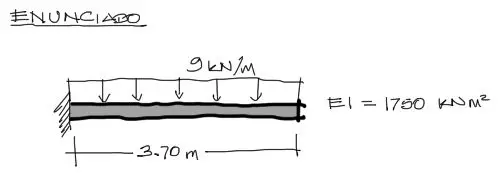
Resolución

La ecuación a aplicar para encontrar deflexiones de una viga isostática producto del Principio de Trabajo Virtual es:

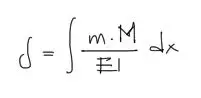
Donde M = Momento flector producto de la carga real; m = momento flector producto de la carga virtual unitaria; EI = rigidez de la viga

Momento flector de la carga distribuida

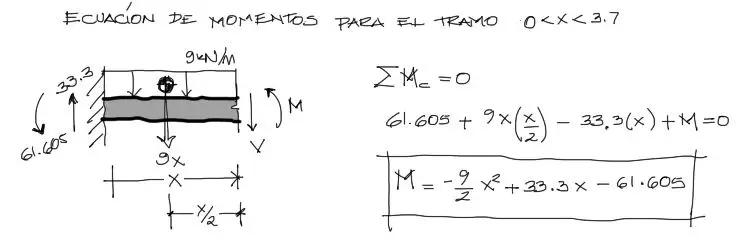
Primero se debe encontrar la ecuación de momento flector producto de la carga real. Para eso primero equilibramos externamente la viga:

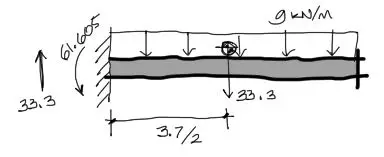
Posteriormente equilibramos el lado izquierdo del corte imaginario para obtener las solicitaciones de cortante y momento flector:

Deflexión en el extremo derecho

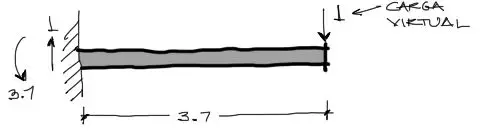
El ejercicio se divide en dos incisos. En este primer inciso se encontrará la deflexión en el extremo derecho de la viga. Para eso encontramos reacciones y momento flector de una carga unitaria apuntando en la dirección en la cual queremos encontrar la deflexión. Las reacciones serán:

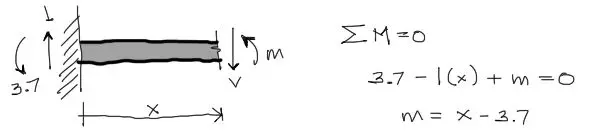
Posteriormente hacemos un corte imaginario a una distancia X del apoyo izquierdo y equilibramos el corte para encontrar V y M:

Posteriormente aplicamos la fórmula de deflexiones por principio de carga virtual. Tanto las ecuaciones de «M» y «m» tienen un dominio entre 0 y 3.7, por lo tanto la integral no necesita dividirse en más que un tramo:

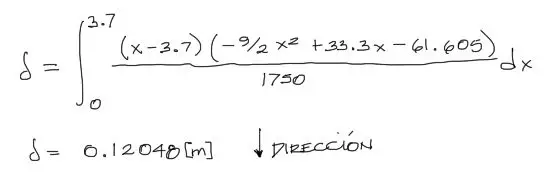
El signo positivo en la solución indica que la deflexión va en el mismo sentido que la carga virtual unitaria.

Deflexión en el centro de la viga

En este caso se deben obtener las ecuaciones de momento flector para la viga cuando la carga virtual se sitúa al centro de la viga. En este caso se debe dividir el análisis de momentos flectores en dos tramos. Se encuentran entonces las reacciones:

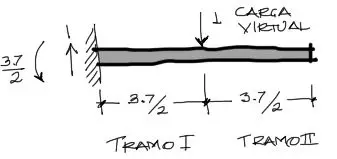
Posteriormente se encuentran las ecuaciones de momento flector. Para el tramo izquierdo (I) se hace un corte a una distancia X entre 0 y 3.7/2. Se tiene entonces:

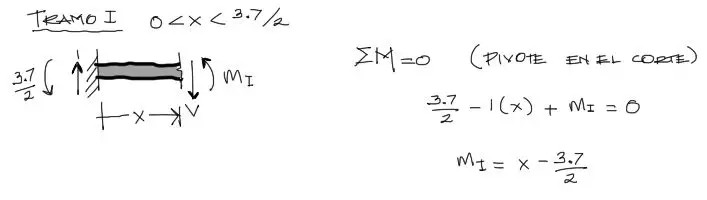
Luego se hace un corte entre 3.7/2 y 3.7 a una distancia X variable. Cabe destacar que se eligió una coordenada que parte del extremo izquierdo de la viga pues esta es la misma coordenada utilizada para el momento flector «M» producto de la carga real. El origen de coordenadas para los momentos flectores para la carga unitaria y la carga real debe ser el mismo.

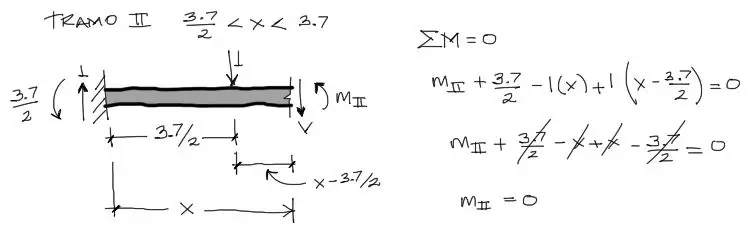
Finalmente se aplica la ecuación integral de PTV para encontrar la deflexión. Debido a que producto de la carga virtual, la viga se divide en dos tramos de análsis (dos dominios), se debe dividir la integral en estos dos dominios para el cálculo de la deflexión.

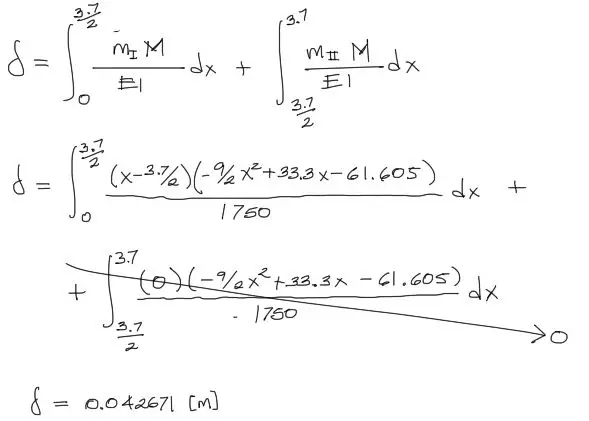
Al igual que en el anterior inciso, el resultado positivo indica una deflexión en el mismo sentido que el de la carga unitaria.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←