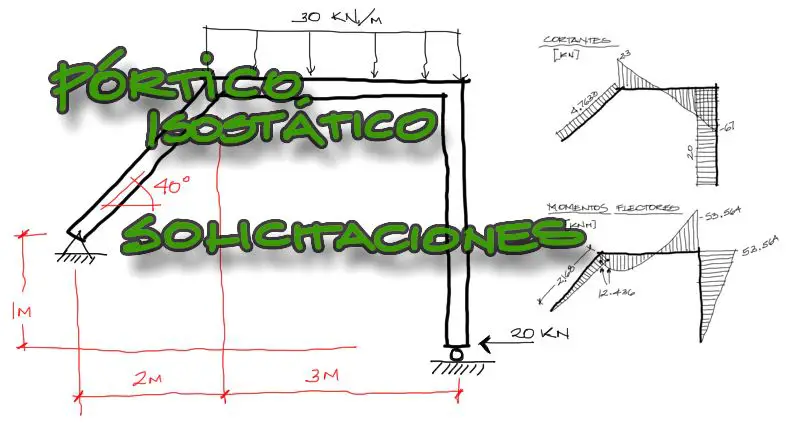
Enunciado

El ejercicio consiste en un pórtico isostático de cual se pide encontrar las reacciones y luego las solicitaciones internas. Las solicitaciones a encontrar son Normales «N», Cortante «V» y momento flector «M».

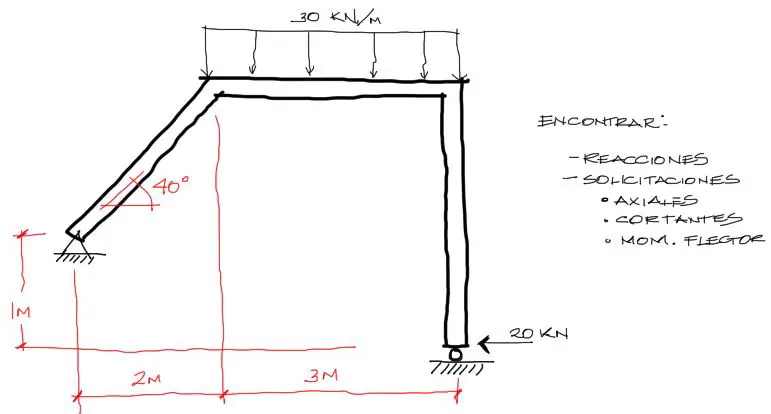
Algunos datos más

Antes de comenzar con la resolución de reacciones, es bueno conocer algunos datos faltantes que aun no tenemos. Por ejemplo, la altura del tramo inclinado. Se puede obtener mediante la relación tangente del triángulo rectángulo. Sabemos que tan(ø) = Cateto Opuesto/Cateto Adyacente. Despejando el cateto opuesto nos queda 2*tan(40) que es la altura del tramo. Luego por pitágoras encontramos la longitud del tramo inclinado.

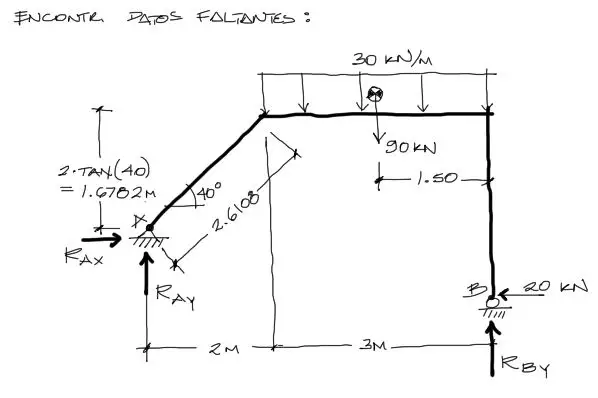
Además necesitamos la resultante de la carga distribuida. esta resultante será la carga distribuida multiplicada por la longitud sobre la cual ha sido aplicada (3m).

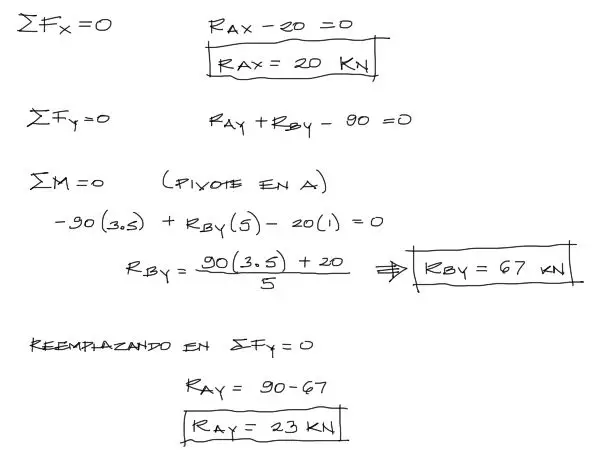
Reacciones

Ahora si procedemos al equilibrio externo. Equilibramos fuerzas en X, en Y y momentos de fuerza.

Solicitaciones internas

Antes de comenzar con las solicitaciones, debemos conocer cuantos tramos de análisis tenemos. Los tramos se definen en función al dominio de las ecuaciones que se encuentren, o sea, cada ecuación de momento flector, cortante o normal servirá para un sector en específico. Un tramo comienza o termina donde exista un cambio de carga, apoyo, articulación o un cambio abrupto de pendiente. En este caso entonces tenemos 3 tramos de análisis:

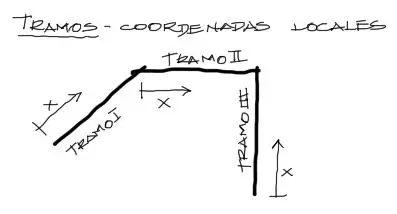
Cada tramo tendrá sus propias coordenadas locales

Tramo I

Antes de equilibrar el corte mostrado en la figura, nos fijamos en la coordenada local que acompaña el eje longitudinal de la pieza. Esta coordenada X’ acompaña el eje longitudinal y está inclinada. Por tanto debemos por comodidad, descomponer primero las fuerzas de reacción del apoyo, respecto a los ejes locales.

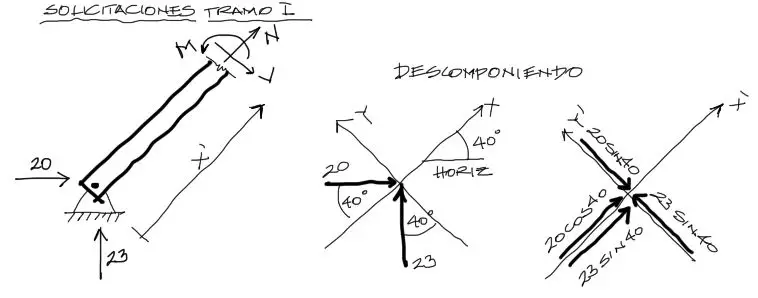
Hecho esto ahora es mucho más sencillo realizar el equilibrio. Al igual que con las cargas externas, utilizamos las 3 ecuaciónes de equilibrio, pero respecto al los ejes locales rotados. Nota que el corte realizado en la figura arriba está ubicado a una distancia VARIABLE X’ respecto del apoyo. Esto se hace para tener no solo las solicitaciones en un punto fijo donde se ubique el corte sino para tener las solicitaciones en forma de ecuación que sirvan para todo el tramo en análisis

Nota que para la suma de momentos igualada a cero, el mejor punto de pivote es el lugar del corte imaginario. De esta forma no entran dentro de la ecuación de equilibrio de Momento de fuerza las Solicitaciones V ni N pues su brazo respecto al pivote es de cero.

Fijate que debido a la coordenada X’ tomada como variable, la ecuación de Momento flector está en función a X’ y variará desde 0 incrementandose linealmente en el otro extremo.

Tramo II

Este tramo es el más complicado por contener una carga distribuida, sin embargo el principio es el mismo. En este caso se escoge una coordenada paralela a los ejes globales pero trasladada al inicio del tramo II. Luego el equilibrio de las fuerzas mostradas es igual que en el anterior caso.

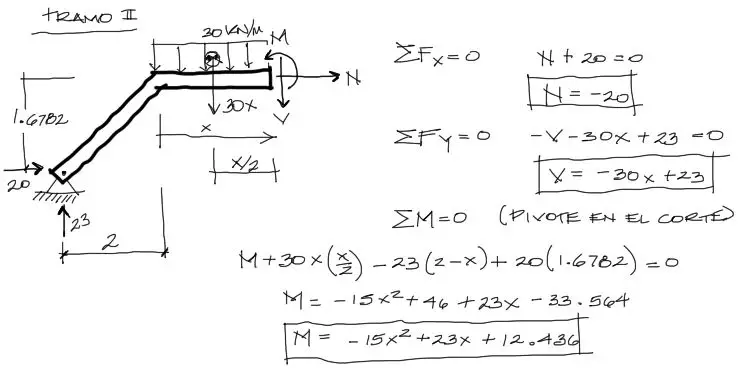
En el caso particular de cargas distribuidas, es conveniente para el análisis de equilibrio, obtener la resultante de la fuerza distribuida actuando en su centroide. Sin embargo el centroide de esta carga varía en función de X.

Tramo III

Para este tramo se escogió arrancar el eje local desde la base del tramo y no desde el extremo superior. Si se escogía arrancar con el eje local desde el extremo superior se habría logrado la continuidad de las ecuaciones pero el análisis hubiera sido algo más largo, pues al equilibrar el miembro izquierdo del corte del tramo 3, tenemos muchas mas fuerzas actuando que en el tramo derecho.

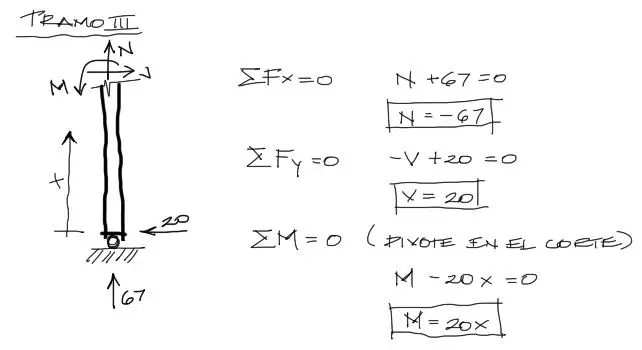
Al equilibrar el tramo a partir del corte inferior el análisis como se ve es mucho más sencillo.

Graficación

Normales

Para las solicitaciones normales, como los tres tramos tienen la solicitación Normal constante, la graficación es directa.

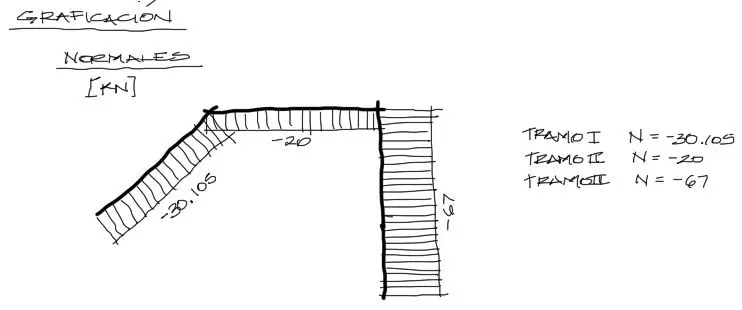
A la derecha se tiene el resumen de las ecuaciones encontradas en el equilibrio interno

Cortantes

Las solicitaciones de Cortante son también sencillas, aunque el tramo II, al contener cargas distribuidas, contiene una ecuación donde los cortantes varían en función de la coordenada local X. Cuando la carga del tramo sea ditribuida constante, la cortante será siempre una recta con pendiente, y el momento flector será parabólico.

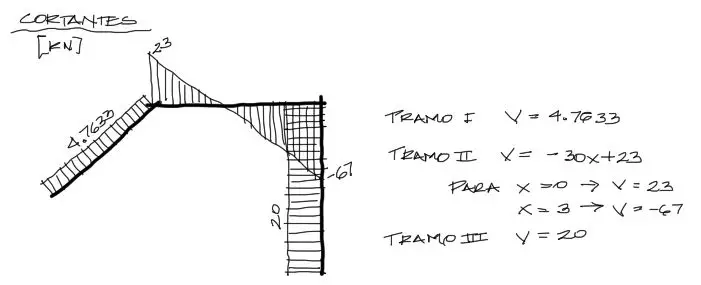
Para graficar el tramo II lo más conveniente es conocer el cortante en los extremos. En este caso cuando X=0 y X=3. Como se sabe que la ecuación es una recta, solo se necesitan dos puntos.

Momentos Flectores

Los momentos flectores cuentan siempre con la graficación más compleja. Esto se debe a que incluso en los tramos sin carga, su diagrama será una ecuación en función de X y no será constante. Para el tramo I se tiene una ecuación de recta, donde igual que con el cortante del tramo II, debemos conocer los valores de los extremos para su graficación. La longitud total del tramo II es de 2.168m, por tanto reemplazando X por 0 y 2.168 obtenemos los momentos flectores mostrados para el tramo I. Nota que si el momento flector obtenido es positivo, se lo dibuja hacia abajo (concordante con la convención invertida utilizada en vigas).

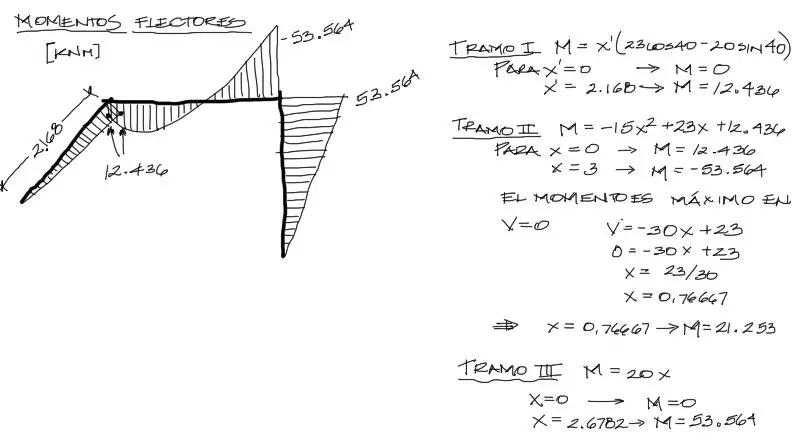
El tramo II es el más complejo, no solo porque la graficación necesite tres puntos por ser una ecuación parabólica, sino porque además de encontrar los valores de los extremos, el tercer punto a encontrar es bueno que sea el máximo valor de la parábola. Para obtener la posición de este máximo, debemos valernos de conceptos de cálculo, donde para la ecuación de una curva, la posición de su máximo o mínimo se encontrará en el sector cuya derivada pase por el punto cero. En nuestro caso conoceremos el punto donde el momento flector se haga máximo conociendo el punto donde el cortante (que es la derivada del momento flector) se haga cero. Es por eso que en el análisis se iguala el cortante a cero y se despeja X. este X encontrado corresponde a la posición de máximo momento en el diagrama de Momentos. Reemplazando este valor de X=0.7667 en la ecuación de momentos flectores se encuentra el máximo de esta curva M = 21.253

Para el tramo III se realiza una operación parecida a la del tramo I, sin embargo en la grafiación el momento flector aparece con signo positivo en el extremo superior, no coincidiendo en signo con el momento de -53.564 obtenido para el segundo tramo. Esto se debe simplemente a que se escogió un sistema coordenado que corta la continuidad en la convención de signos del sistema.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←