Enunciado

Se plantea obtener los momentos flectores y cortantes de losa mostrada a continuación

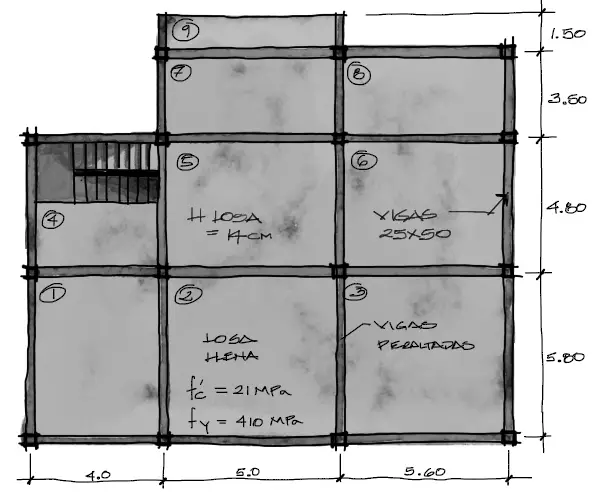
Las cargas a las que estará sometida la losa son:
– Carga muerta no estructural = 4KN/m2
– Carga viga = 2 KN/m2

Las alturas de losa y vigas se determinaron en el artículo anterior:
– Altura mínima de losas llenas apoyadas en los bordes

Resolución

Para este caso utilizaremos el método de Coeficientes o método de Marcus para la determinación de los momentos positivos y negativos en losa. Este método fue publicado en 1963, sin embargo ha sido útil y satisfactorio por bastante tiempo y lo sigue siendo académicamente hoy en día.

La teoría acerca del método con las tablas en buena resolución se encuentran en el enlace TEORÍA DE SOLICITACIONES EN LOSAS EN 2Dir APOYADAS EN SUS BORDES.

Solicitaciones en cuadrante 3 (el más crítico)

Si bien se deberían utilizar luces libres para el cálculo de solicitaciones en losas, para propósitos prácticos se analizarán las solicitaciones para los paños de losa medidos de eje a eje. En este caso la losa en análisis es de 5.80×5.60 metros en cada dirección.

Por la configuración de la losa, tenemos dos tramos contínuos y dos discontinuos, para lo que debemos buscar este caso de coeficientes en las tablas de Marcus:

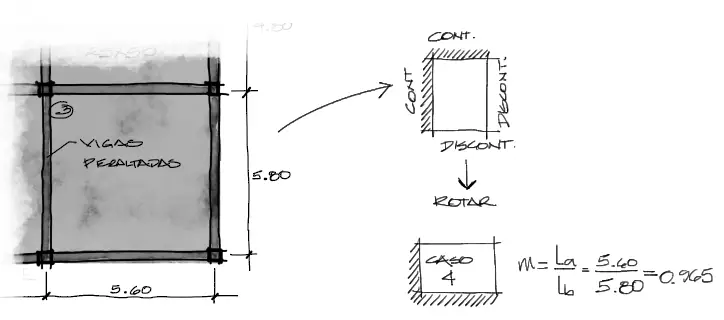
El caso del paño 3 corresponde al caso 4, con un lado largo y un lado corto contínuo. El mayor problema de las tablas de Marcus es que debemos distinguir a detenimiento cual es el lado largo y corto en las tablas y correlacionarlas con el caso real. Luego obtenemos la relación m=Lado corto/lado largo.

Coeficientes Ca y Cb

Existen 3 tablas de coeficientes para encontrar los momentos flectores en el paño:
– Tabla de momentos negativos de carga muerta +carga viva
– Tabla de momentos positivos por carga muerta
– Tabla de momentos positivos por carga viva

Las tablas de Marcus tienen relaciones “m” saltadas de 5 en 5 centécimas, por lo que deberemos interpolar nuestros valores de Ca y Cb a partir del “m” obtenido en la mayoría de los casos, como en el presente. Comenzamos con la tabla de coeficientes para momentos negativos:

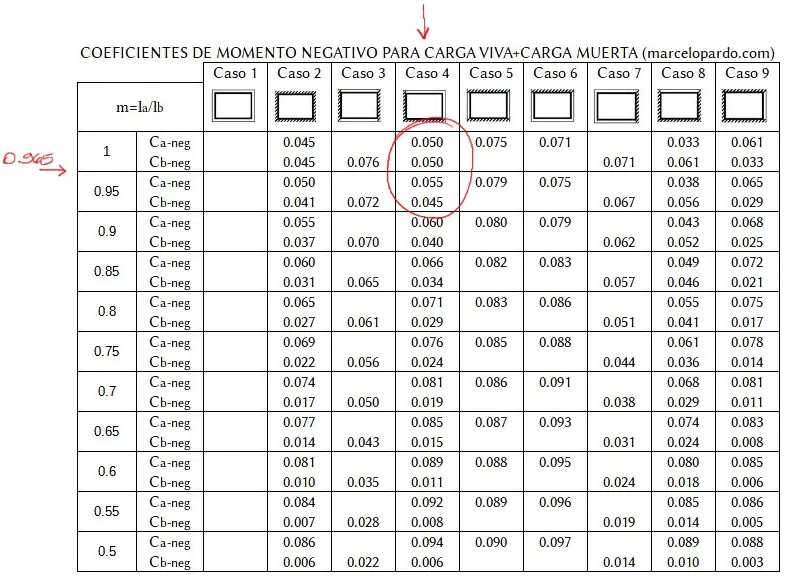
La interpolación es lineal y puede realizarse a partir del siguiente razonamiento:

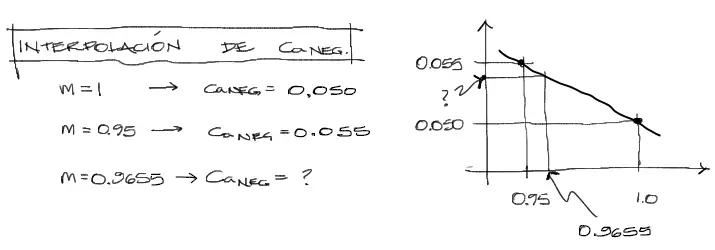
Se pueden encontrar los valores de Ca y Cb a partir de la ecuación de la recta, con “m” equivalente a “x” y con Y equivalente a los valores de Ca y Cb uno a la vez. Se tiene entonces para Ca:

Y de la misma manera para Cb:

Para los coeficientes de momentos positivos tanto de cargas muertas como de cargas vivas se realiza la misma interpolación, por lo que no se repetirá el procedimiento acá. Los resultados son:

Momentos Flectores

Antes de obtener los momentos flectores, debemos conocer la magnitud del peso propio de losa. Para eso multiplicamos el espesor de la losa por el peso específico del hormigón (24 KN/m3). Se tiene entonces:

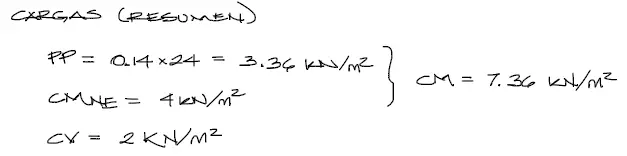
Posteriormente a partir de las fórmulas de la teoría de los coeficientes de Marcus, se tiene que los momentos responden a M = C*q*L² donde:
– C es el coeficiente Ca o Cb
– q es la carga distribuida en la losa
– L es la longitud en la dirección “a” o “b” respectivamente

Por tanto los momentos negativos con las cargas muerta y viva sumadas son:

Para los momentos flectores positivos se repite el proceso pero para cargas muertas separadas de las cargas vivas y luego sumar ambos momentos:

En el enunciado no se pide que se mayoren por lo que se hará la suma algebraica de los momentos flectores muertos y vivos sin factorizar.

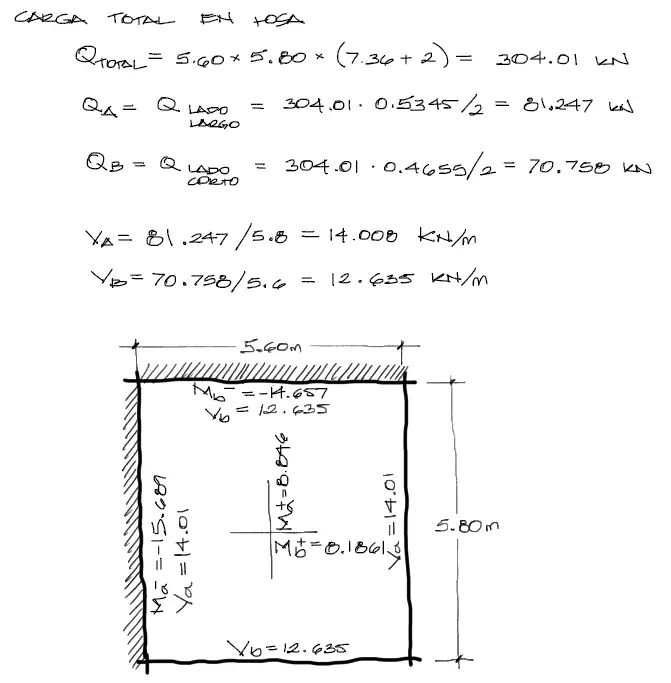
Gráficamente, los momentos flectores obtenidos arreglados en el paño de losa se ven de la siguiente manera:

Debe entenderse que los momentos flectores negativos solo se aplican siempre a los laterales contínuos. Los discontínuos en teoría reciben un momento negativo igual a cero por su naturaleza articulada (o pseudoarticulada cuando se apoyan en vigas). Cuando la losa se apoya monolíticamente sobre vigas el autor indica que al momento negativo en el apoyo discontinuo se le asigne 1/3 del momento positivo en la misma dirección.

Fueza Cortante

Cuando se quieran obtener los cortantes a partir de los coeficientes de Marcus, se debe utilizar la cuarta tabla bajo el mismo razonamiento de las anteriores. Interpolando los valores de Wa y Wb de la cuarta tabla tenemos:

Estos coeficientes Wa y Wb representan el porcentaje de carga que se repartirá entre el los dos lados cortos y los dos lados largos de la losa. Así, la carga que se reparte por ejemplo entre los dos lados largos de la losa será Area*carga*Wa. Luego esta expresión deberá dividirse entre dos para repartir la carga encontrada entre los dos lados largos. El procedimiento se repite para el lado corto de la misma manera.

Finalmente el cortante uniformemente distribuido a lo largo de los bordes es la carga Q dividida a lo largo de la longitud del borde considerado (en este caso Qa dividido entre lado B y viseversa). Se tiene entonces:

Programa en Javascript

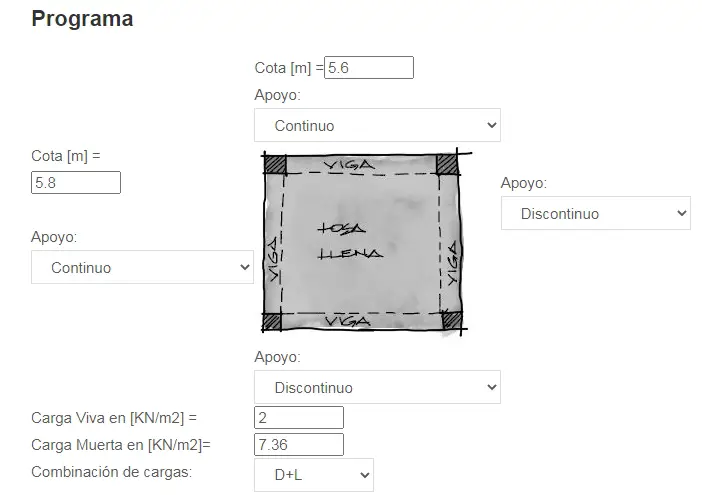
Todo el procedimiento anteriormente descrito, menos mal es lo suficientemente mecánico como para ser programado. El programa pide como ingreso de datos las longitudes de los lados de la losa, la continuidad o discontinuidad de cada lado y las respectivas cargas. El enlace al programa es el siguiente:
– PROGRAMA DE SOLICITACIONES EN LOSA APOYADA EN LOS BORDES ARMADA EN 2 DIRECCIONES POR MÉTODO DE COEFICIENTES

La ventaja de este programa es que no necesitamos acomodar la losa con el borde más largo horizontalmente.

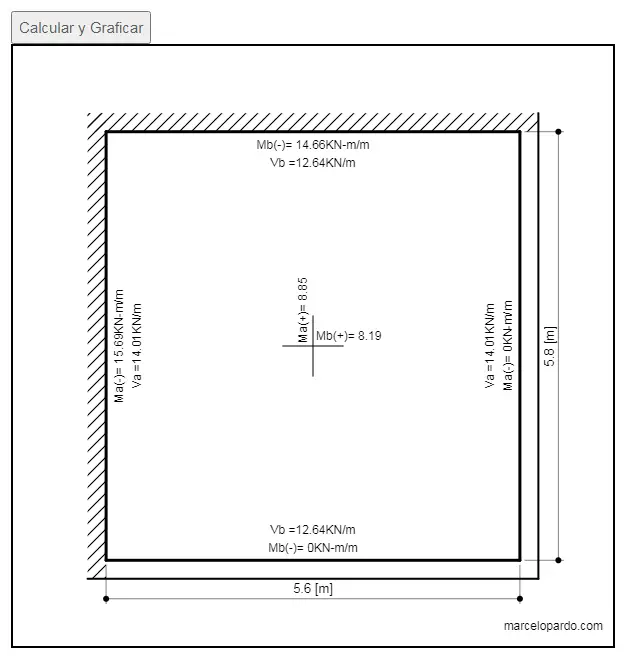
A partir del ingreso de los mismos datos resueltos líneas arriba, obtenemos los mismos resultados con el programa luego de presionar el boton de CALCULAR Y GRAFICAR.

Si te sirvió la publicación o deseas que mejore algún aspecto del programa, deja tu comentario debajo.

Vídeo

Si prefieres ver la explicación didáctica en vídeo, publiqué uno al respecto incluyendo el uso del programa.

autor: Marcelo Pardo

←←← Teoría de solicitaciones en losa 2D por Marcus ←←← →→→ Programa: Solicitaciones de losas en 2D →→→

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO ←←←