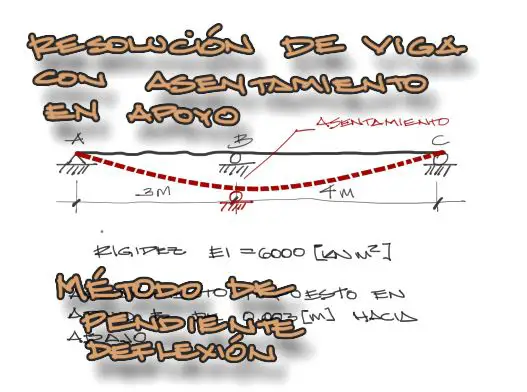
Enunciado
Se plantea la viga siguiente, con una rigidez constante de 6000 KNm2 y con un asentamiento impuesto hacia abajo en el apoyo B de 3mm. Resolver las solicitaciones de cortante y de momento flector en la viga.
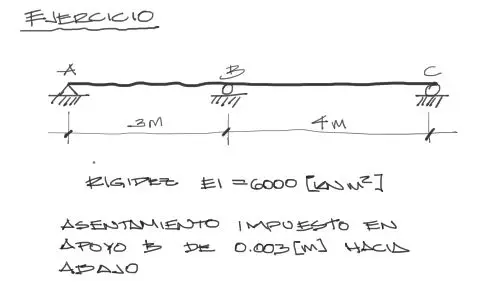
Solución
Para entender el método, es conveniente que antes de resolver el ejercicio repasemos la TEORÍA DEL MÉTODO DE PENDIENTE DEFLEXIÓN.
Ecuaciones de pendiente deflexión
Las ecuaciones genéricas del método de pendiente deflexión son las siguientes:
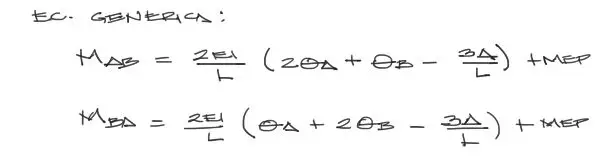
De todas estas variables, las conocidas son EI = 6000, las longitudes de ambos tramos: L1 = 3m y L2=4m. Además los MEP tanto del tramo AB como de BC son nulos por la ausencia de cargas en la viga.
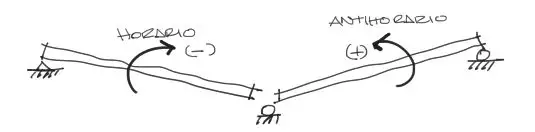
La variable Δ para el tramo AB será negativa y valdrá -0.003 ya que el asentamiento en B produce un giro horario en el tramo AB. Lo contrario sucede en el tramo BC: El mismo asentamiento en B de 0.003 hacia abajo produce un giro positivo antihorario en el tramo AB.
Entonces reemplazando todos estos valores en las ecuaciones de pendiente deflexión para ambos tramos:

Notemos además que por las condiciones de contorno (por definición) los apoyos fijos y móviles en los extremos de una viga siempre generan momento flector nulo en la viga en ese punto. Por eso Mab y Mcb se hacen cero.
Hasta el momento se tienen 4 ecuaciones y 5 incógnitas. La quinta ecuación la obtenemos del equilibrio entre ambos tramos. Se supone que la continuidad del tramo AB con BC generan que los momentos en el punto de unión sean iguales y de signo opuesto. Por tanto:
El sistema de ecuaciones
Las cinco ecuaciones anteriores pueden escribirse en forma matricial de la siguiente manera, llevando todos los términos con variable al lado izquierdo y los términos independientes (una vez desarrollados los paréntesis) al lado derecho:
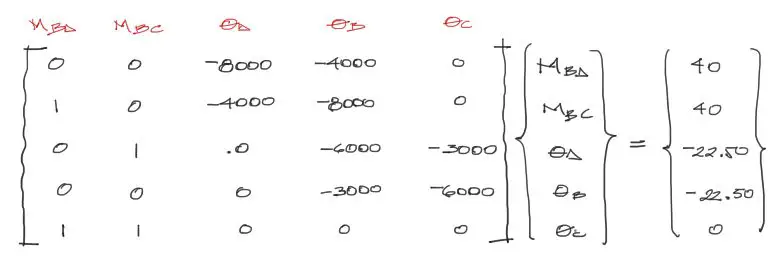
Este sistema se resuelve fácilmente a partir de [A]{x}={b} entonces —> {x} = inv([A])*{b}. Queda entonces:

Cortantes en los tramos
Ya se conocen los momentos flectores en los extremos de cada tramo:
- Mab = 0
- Mba = 15
- Mbc = -15
- Mcb = 0
Se puede proceder entonces con el equilibrio de cada tramo a partir de:
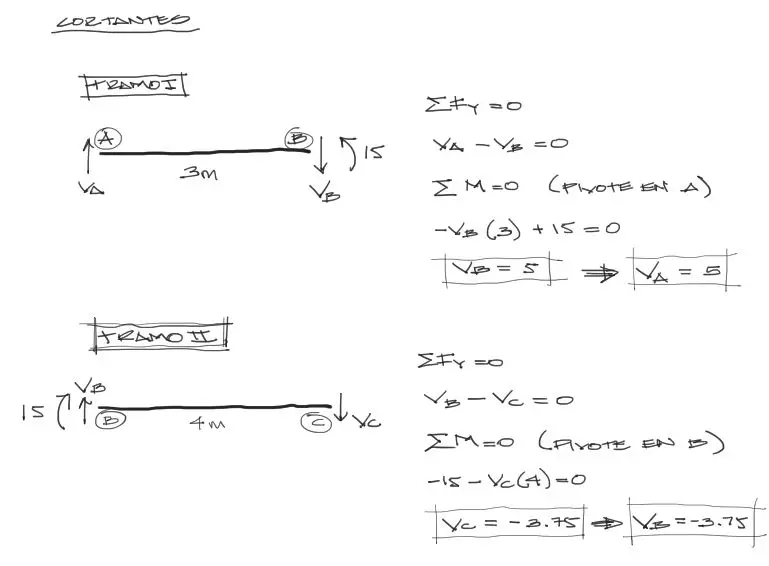
Debido a la ausencia de cargas externas la resolución de los cortantes extremos es rápida. Notemos que adoptamos la convención de signos de cortante concordante con la de los diagramas de graficación de cortantes y momentos flectores.
Graficación de diagramas
El diagrama de cortante es constante en el tramo I a partir de Va = y; Vb = 5 y similar sucede en el tramo II:
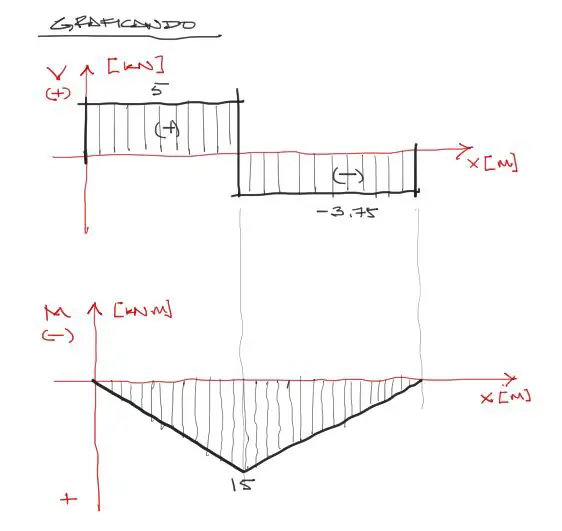
Para el momento flector se razona de la siguiente manera. La viga no lleva cargas de ningún tipo en ningún tramo, por tanto el diagrama es recto y contínuo en cada tramo. El momento en BA y BC genera tracción de las fibras inferiores en ambos lados, por tanto en el diagrama el momento flector vale 15KNm positivo para ambos tramos.
autor: Marcelo Pardo

