Enunciado
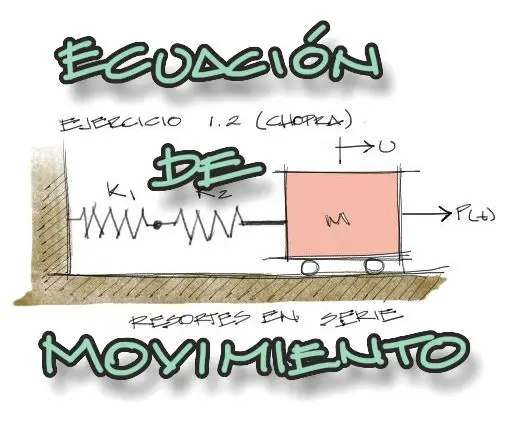
Determinar la ecuación de movimiento del sistema mostrado. Los resortes están acomodados en serie.
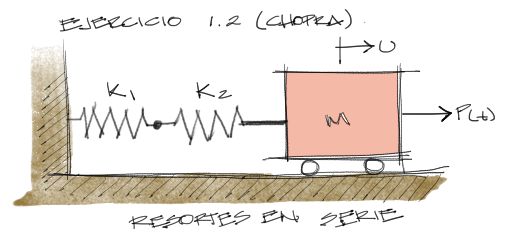
Solución
Si dibujamos un diagrama de cuerpo libre con las fuerzas que actuan en la masa, se tiene:
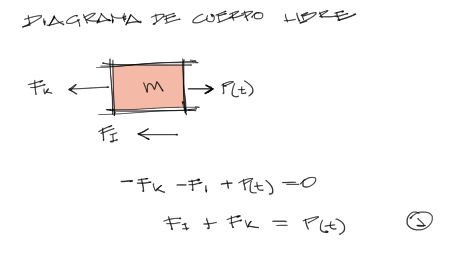
Las fuerzas actuantes son:
– FI: Fuerza ficticia de inercia (en el sentido contrario al movimiento. – FK: Fuerza del resorte. – P(t): fuerza externa en la dirección del movimiento.
A diferencia del anterior ejercicio de resortes acomodados en paralelo, en este caso las fuerzas de ambos resortes están dispuestos en serie. Por tanto la fuerza del resorte 1 será igual a la fuerza del resorte 2. Por tanto FK1 y FK2 serán denotados simplemente por FK. Además sabemos que la fuerza de un resorte es igual a su módulo K por la deformación u.
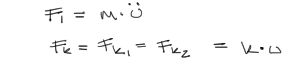
Además, si bien las fuerzas son iguales, las deformaciones de ambos resortes se suman en una deformación total “u”, gracias a la disposición en serie de ambos resortes.

A la vez, la deformación de un resorte es igual a u = F/K. Si reemplazamos las deformaciones u1 y u2 dentro de la suma de deformaciones, se obtienen finalmente:

En el análisis anterior las fuerzas se anulan pues, como se mencionó anteriormente, son iguales.
Ya obtenida la rigidez de la composición de ambos resortes, se puede reemplazar K dentro de la fuerza producto de los resortes y además la fuerza ficticia inercial como el producto de la masa por la aceleración d2u/dt2.

Casos prácticos similares
Si bien esta situación es muy raramente encontrada en la práctica, puede darse algún caso de una columna que cambia de sección y por tanto cuenta con dos rigideces distintas, acomodadas como se muestra a continuación.
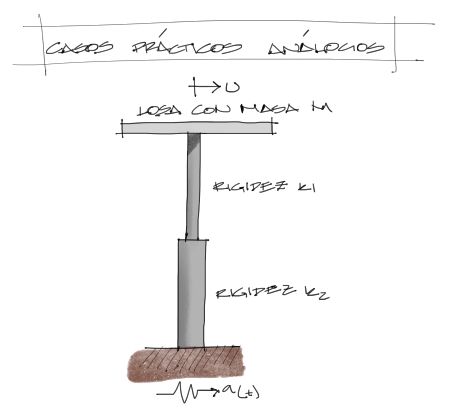
Puede encontrarse este tipo de situaciones en tanques de agua elevados por columnas donde los tramos de columnas varíen en sección en la interesección con vigas rigidizadoras.
autor: Marcelo Pardo