Elemento de barra

El elemento de barra en 3 dimensiones es muy similar al elemento en 2 dimensiones, sin embargo debe contemplar solicitaciones adicionales de torsión y de momento flector en la dirección perpendicular al plano de análisis de un pórtico 2D.

Este planteamiento añade tres grados de libertad a cada nudo del elemento de barra. Por simplicidad la mayoría de los programas trabajan con elementos de barra de solo dos nudos, uno en cada extremo.

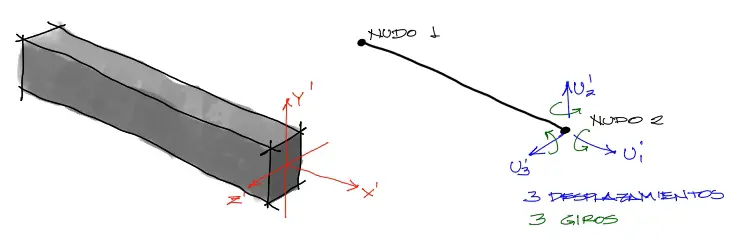
Grados de libertad y solicitaciones

Los elementos de barra en la bibliografía suelen trabajar con el eje local x’ alineado con el eje longitudinal de la barra. El eje y’ suele alinear con el eje vertical de la sección transversal de la barra y el eze z’ con la horizontal de la sección transversal, como se muestra en la imagen siguiente:

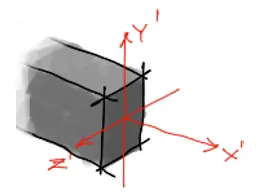
Concordante con estos grados de libertad, las solicitaciones en una barra van alineados con esos grados de libertad:

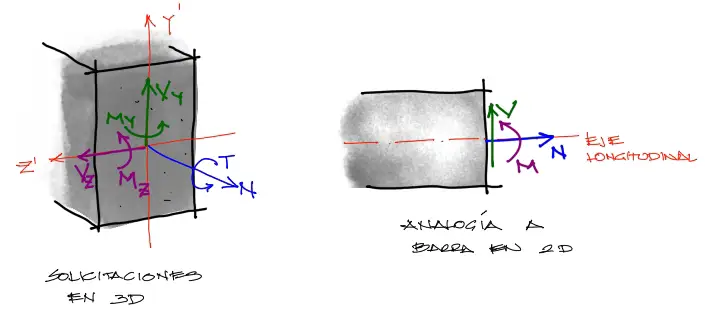
Se nota la complejidad que adquieren estos grados de libertad al incrementarse a 6. Cuando se trabajaba en 2 dimensiones, las solicitaciones en consideración eran solamente la axial N, Cortante Vy y momento flector Mz, que por simplicidad llamabamos simplemente N, V, M. Ahora necesitamos direccionar cada cortante y momento respecto de sus respectivos ejes locales.

Variables

Las propiedades de sección que estan involucrados en la matriz de rigidez de la viga son:

• L: Longitud de la barra
• A: Superficie de sección transversal
• Iy: Inercia de la sección respecto al eje Y’
• Iz: Inercia de la sección respecto al eje Z’ (giro respecto a Z’)
• J: Módulo de torsión de la sección transversal
• G: Módulo de corte
• E: Módulo de elasticidad
• v: módulo de Poisson

A la vez el módulo de corte y el módulo elástico están relacionados por la siguiente expresión:

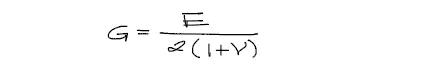
Además la expresión del módulo de torsión puede encontrarse para varias secciones. Para las secciones más típicas, el módulo J tiene las siguientes relaciones:

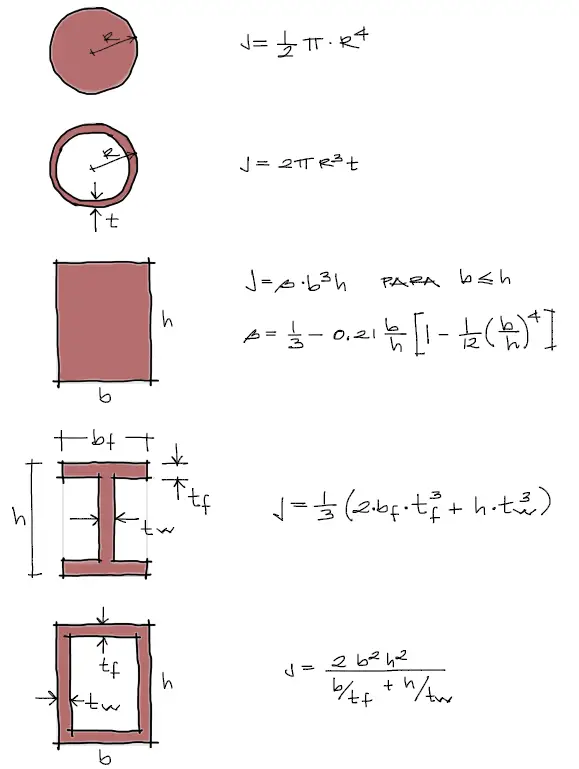
Las variables de inercia pueden obtenerse por los métodos tradicionales, y pueden consultarse en la TABLA DE CENTROIDES E INERCIAS DE FIGURAS TÍPICAS donde simplemente debe reemplazarse el eje X de la tabla por el eje Z de este apartado.

Matriz de Rigidez

Finalmente la matriz de rigidez de un elemento de barra de 2 nudos es:

Qué sigue

Luego de haber construido la matriz de rigidez de un elemento, éste deberá someterse a varias transformaciones de coordenadas porque en muy pocas situaciones la barra estará dirigida a lo largo del eje X como se muestra en sus coordenadas locales. Estas transformaciones se verán en el siguiente artículo.

→→→ Transformación de coordenadas de [K] en 3D →→→

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←