Enunciado

El ejercicio siguiente ya pertenece a un conjunto de ejercicios más complejos que no podrían resolverse mediante métodos clásicos.

Se pide encontrar el diagrama de momentos flectores y cortantes de la viga mostrada, apoyada al centro sobre dos resortes de rigideces de 4000[KN/m]. Todos los datos se muestran en la figura.

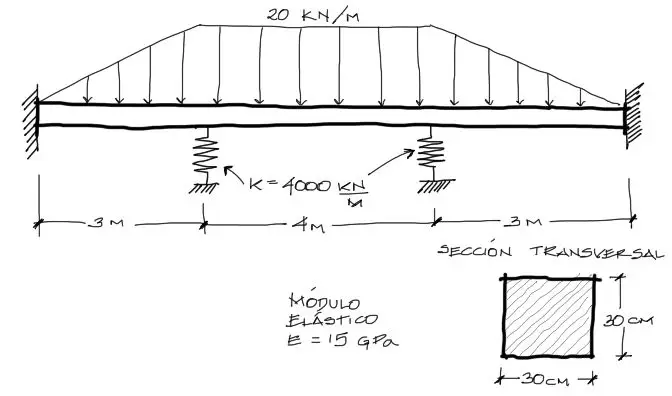
Solución

Análisis de datos del problema

Antes de proceder con la resolución por el método matricial o de rigidez, se deben analizar los datos. El convertir todos los elementos a las mismas unidades es primordial, así como calcular los datos que falten.

El módulo elástico debe estar en KN/m² pues todos los datos están en estas unidades. Por otro lado la sección transversal tb debe convertirse a metros y encontrar la inercia.

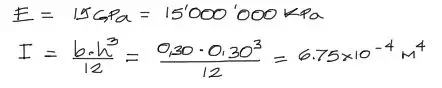
División de la viga y grados de libertad

El siguiente paso para aplicar el método de rigidez consiste en la división de la viga en elementos unidos por nudos. Cada división debe hacerse en cada cambio de carga, en un apoyo, o donde termine o comience una carga. En este caso hacemos la división en:

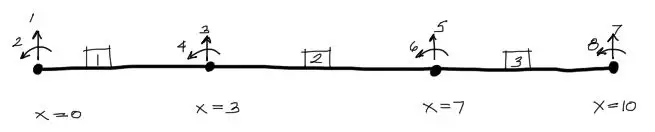
Por otro lado cada nudo tiene 2 grados de libertad. No se considera el grado de libertad horizontal pues se trabajará con elementos de viga cuyo desplazamiento o deformación horizontal no nos interesa por ser despreciable. Los grados de libertad impares son de desplazamiento y los pares de giro.

Matrices de rigidez de cada elemento

Se calculan las matrices de rigidez de cada elemento (3 elementos) en base a la teoría

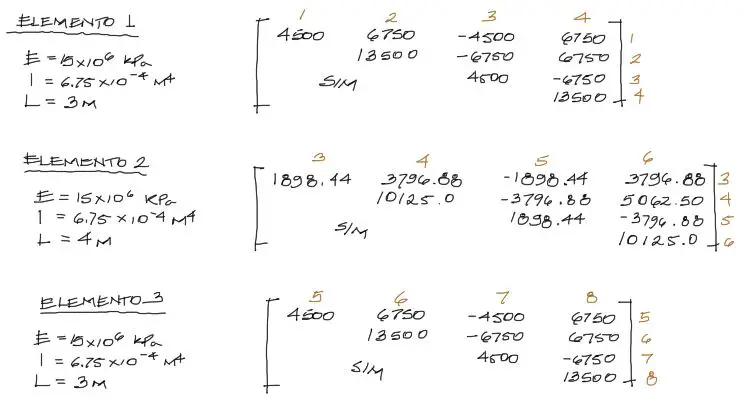
En las matrices arriba, «SIM» denota «simétrica»

Ensamblaje de la matriz de rigidez

Si pones atención en los grados de libertad de la figura tercera de este artículo, estos grados de libertad se repiten en las matrices de rigidez de cada elemento. Estas posiciones de las matrices de rigidez de cada elemento deben transportarse a una matriz global de dimension 8×8 (igual al número total de grados de libertad de la estructura).

Si dos valores de las matrices de rigidez de cada elemento caen dentro de la misma casilla dentro de la matriz de rigidez global, los valores se suman.

Cargas

Cada tramo de la viga tiene un solo tipo de carga. Se supone que las divisiones de elementos finitos se hizo pensando en este factor. En este caso solamente tenemos en los tramos cargas distribuidas. Debemos mediante tablas de momentos de empotramiento perfecto, buscar las acciones equivalentes de momento y fuerza en los extremos de vigas empotradas con cargas similares a las de cada tramo. Se tiene para nuestro caso:

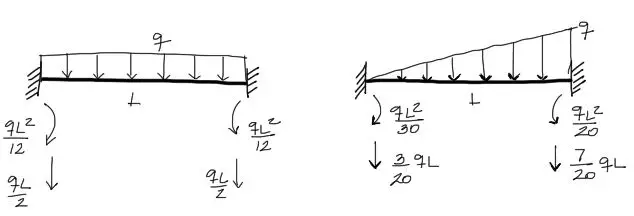
Aplicando estas fórmulas a cada uno de nuestros tramos se tienen los siguientes valores de cargas equivalentes en los extremos de cada tramo:

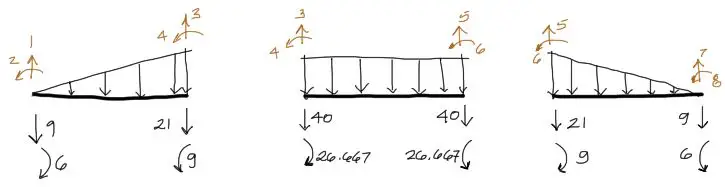
Nota que las cargas equivalentes van en sentido contrario a las reacciones en los extremos del tramo imaginariamente empotrado.

Cara una de estas cargas debe ir en el respectivo grado de libertad dentro del sistema de ecuaciones 8×8

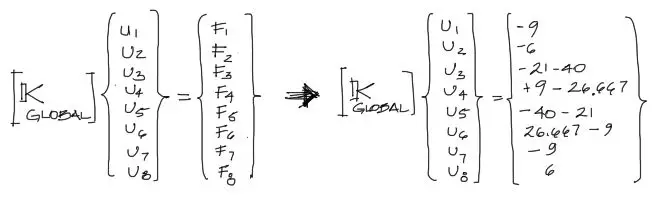
Nota que cuando introducimos las cargas dentro del sistema, respetamos la convención de signos: positivo arriba; Positivo antihorario

Reacciones y resortes

El sistema de ecuaciones anterior está aun incompleto. Si intentaramos resolverlo, obtendríamos infinitas soluciones pues el sistema es singular (determinante cero). Para poder «apoyar» la matriz, debemos imponer condiciones de contorno. Estas condiciones de contorno corresponden a las reacciones del sistema. Primeramente colocaremos nuestras reacciones incógnita dentro del sistema. Estas reacciones deben ir en los grados de libertad correspondiente. Para fuerzas verticales, los grados de libertad de desplazamiento vertical (impares); para los momentos de fuerza, los grados de libertad de giro (pares).

Las incógnitas se suman al vector de fuerza encontrado en el anterior inciso.

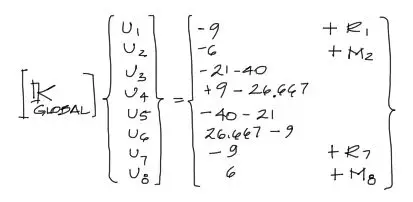
El sistema de ecuaciones arriba estaría completo si se tratara de un problema con apoyos convencionales. Sin embargo en nuestro ejercicio existen resortes. Estos resortes ejercen una fuerza opuesta al desplazamiento del nudo. Si el nudo 3 se desplaza hacia abajo (negativo), la reacción de estos resortes será hacia arriba (positiva). Por otro lado sabemos que los resortes ejercen una fuerza equivalente al desplazamiento de uno de los extremos del resorte. todos conocemos la fórmula de física F=Kx. Para nuestro problema esa fórmula se convierte en F3 = -4000·U3 y F3 = -4000·U5 respectivamente para el grado de libertad 3 y 5:

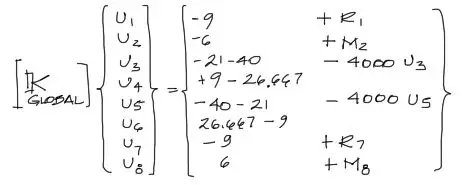
Restricción de los desplazamientos

Donde los grados de libertad no se mueven verticalmente ni giran, los desplazamientos se deben hacer cero. Ese es el caso de nuestros empotramientos en los extremos. Entonces:

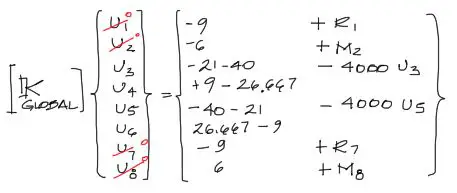
Resolución del sistema

Hasta aquí se tiene todo el sistema definido. Queda la resolución del sistema. Para hacer esto, una de las formas más convenientes consiste en anular las filas y columnas de los grados de libertad restringidos. Esto significa multiplicar por cero las columnas 1,2,7,8 y eliminar temporalmente estas mismas filas pues no se necesitan sus respectivas ecuaciones.

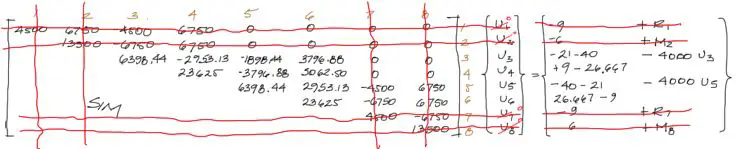
Quedando:

Nota que aun tenemos incógnitas a ambos lados de la ecuación. Esto puede resolverse pasando las incógnitas con sus coeficientes al lado izquierdo de la ecuación a sus respectivas posiciones en el sistema de ecuaciones:

Ahora el sistema se resuelve mediante cualquier método. Uno de los más eficientes es el de Gauss-Jordan. Resolviendo entonces, tenemos los desplazamientos y giros:

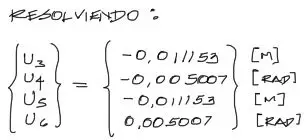
Algo más que podemos sacar del sistema de ecuaciones son las reacciones de nuestros apoyos, incluyendo las reacciones de nuestros resortes.

Para eso, con los desplazamientos de los nudos 3,4,5,6 conocidos, reemplazamos estos datos dentro del sistema de ecuaciones original de 8×8, de la siguiente forma

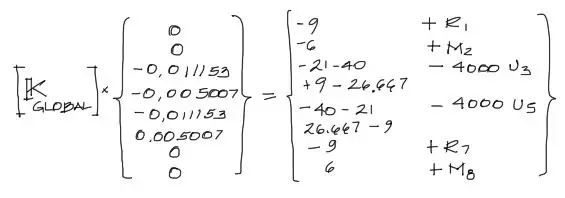
El miembro izquiero de la ecuación es completamente operable pues no hay incógnitas. Multiplicando se tiene:

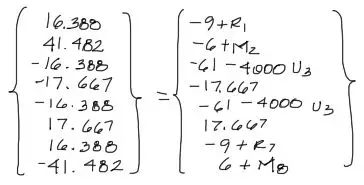
De esta igualdad podemos despejar las incógnitas. Recuerda que la fuerza de un resorte es igual al módulo k = 4000 por el desplazamiento de un extremo. Por tanto esta expresión -4000·u3 y -4000·u5 es igual a la reacción del resorte.

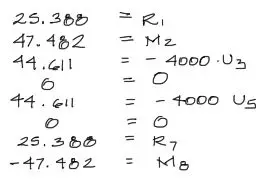
Con todos estos resultados podemos dibujar lo obtenido. La convención de signos es siempre positivo arriba y positivo antihorario

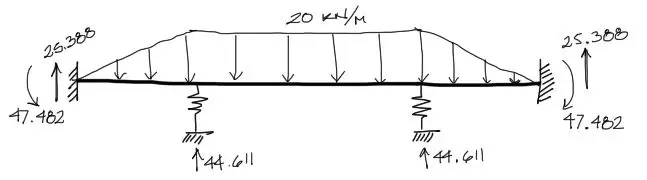
Diagramas de momento flector y cortante

A continuación procede un análisis de postproceso para encontrar las solicitaciones en los elementos de viga. Este trabajo lo puedes leer en la siguiente publicación siguiendo el enlace: SOLICITACIONES DE MOMENTO Y CORTANTE EN VIGA APOYADA EN RESORTES O LECHO ELÁSTICO

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS←←←