Breve teoría

Para la conocer la deducción de las fórmulas del método de pendiente deflexión puedes dirigirte a:

→→→DEMOSTRACIÓN DE FÓRMULAS DEL MÉTODO DE PENDIENTE DEFLEXIÓN→→→

En este apartado sólamente mencionaré las fórmulas que se utilizan para la resolución de ejercicios bajo este método y su uso.

Fórmulas

El método de pendiente deflexión cuenta con dos fórmulas básicas:

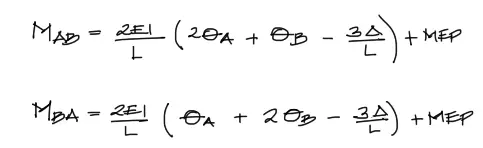
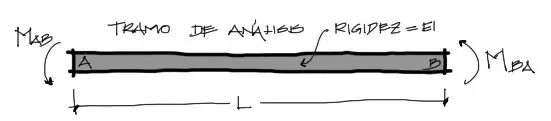
A y B son los dos extremos de un tramo de la viga entre dos apoyos. Como las vigas hiperestáticas tienen más de un tramo, en una viga de dos tramos se tendrán por ejemplo la dupla de momentos (Mab – Mba) y para el siguiente tramo la dupla de momentos (Mbc – Mcb).

Convención de signos

La convención de signos para este método suele ser uno de los aspectos de mayor conflicto a la hora de aplicar las ecuaciones de arriba

Con respecto a los momentos en los extremos Mab y Mba, estos llevarán signo positivo si rotan en el sentido antihorario. Inicialmente, cuando no se conocen los valores de estos momentos, se asume que giran en el sentido positivo.

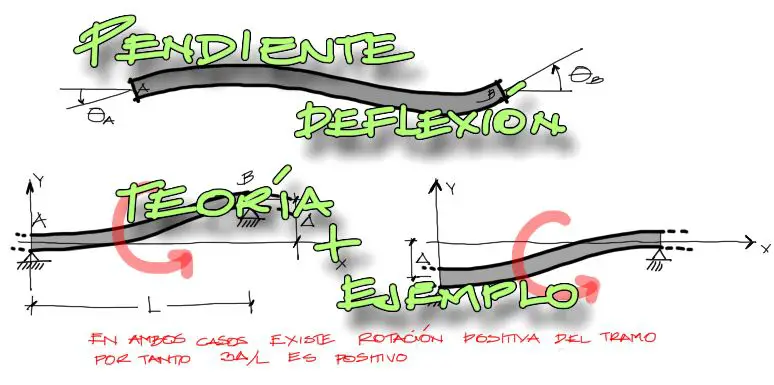
Cuando se trata de giros, estos se miden en radianes [rad]. En las ecuaciones de pendiente deflexión se cuenta con los giros en los extremos de cada tramo. Estos giros al igual que los momentos flectores, se consideran positivos si giran en el sentido antihorario.

Tal vez el elemento que trae más confusión respecta al asentamiento Δ. Esto se debe a que por un lado la fórmula de pendiente deflexión ya lleva el signo negativo. Por otro lado, el signo de Δ NO depende directamente de si el asentamiento va hacia arriba o hacia abajo.

La manera de analizar el signo de la expresión 3Δ/L es la siguiente. Se debe analizar el tramo en su conjunto. No importa si el asentamiento se genera en el tramo izquierdo o en el tramo derecho, lo que importa es si el asentamiento en cualquiera de los dos extremos produce un «giro» global del tramo en sentido horario o antihorario.

Por ejemplo, la expresión 3Δ/L será positiva en cualquiera de las dos siguientes situaciones, para el tramo AB:

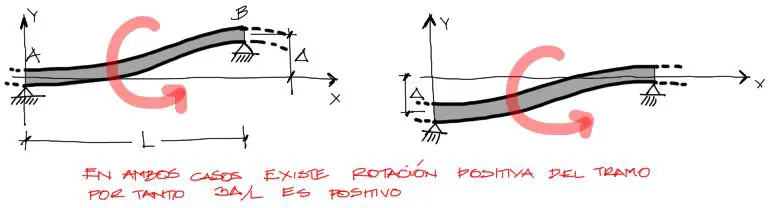
Por el contrario esta expresión será negativa cuando se de cualquiera de las siguientes situaciones de asentamiento:

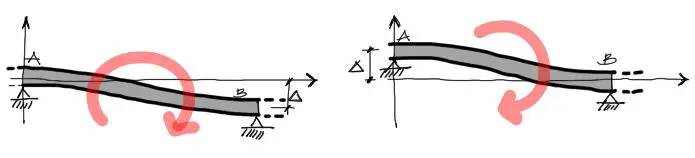
Finalmente, la convención de signos de los momentos de empotramiento perfecto MEP es igual al de los momentos Mab y Mba, positivo antihorario y negativo horario. Sin embargo suele suceder casi siempre que bajo cargas convencionales, el momento de empotramiento perfecto izquierdo es antihorario y el derecho horario. Esto se debe a que las cargas convencionales verticales hacia abajo generan una reacción de momento en los extremos que describen ese comportamiento:

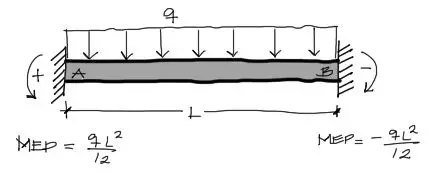
Por ejemplo en la figura, se ve el tipo más común de carga y MEP. Para ver otros momentos de empotramiento perfecto típicos, te invito a visitar la publicación:
Tabla de Momentos de Empotramiento Perfecto

Procedimiento

Se deben seguir los siguientes pasos:

• Separar la viga en tramos ENTRE APOYOS.
• Escribir las ecuaciones genéricas de pendiente deflexión para cada tramo
• Calcular los Momentos de Empotramiento Perfecto para la carga de cada tramo.
• Determinar cuales son las condiciones de borde del problema: En empotramientos= Giro igual a cero. En apoyos fijos y móviles en extremos = Momento cero.
• En los apoyos sumar los momentos de tramos que llegan al apoyo e igualarlos a cero (ver ejemplo)

Se formará un sistema de ecuaciones con igual número de ecuaciones que de incógnitas que puede resolverse mediante cualquier método. Los resultados encontrados serán momentos en los apoyos y giros en los apoyos. A partir de estos dos datos se pueden encontrar los diagramas de momentos flectores y cortantes con el procedimiento de postproceso:

Cómo obtener diagramas de M y V a partir de momentos en los extremos

Ejemplo

Enunciado

Para tener una idea más clara del método, se propone el siguiente ejercicio:

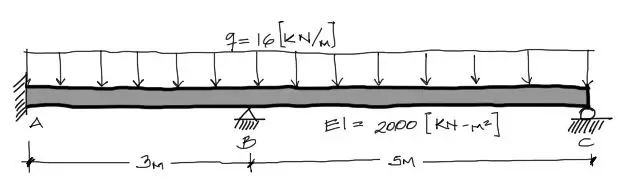
Se debe encontrar los momentos en los puntos A, B, C

Solución

Para este ejercicio, se plantean las ecuaciones de pendiente deflexión para cada tramo:

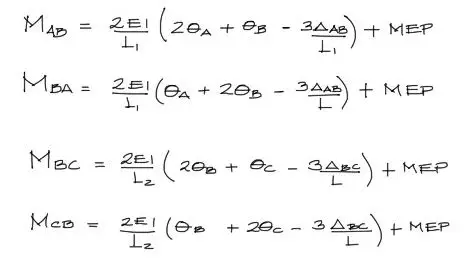
Además por las condiciones del problema, las condiciones de contorno dictan que:

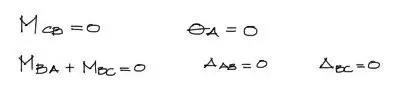
El giro en el punto A es cero debido a que en el empotramiento la viga es incapaz de rotar. Por otro lado el momento Mba es igual pero opuesto en signo al momento Mbc. Esta oposición de signos se da para cumplir el equilibrio de la fórmula. Finalmente, como no existen asentamientos en este ejemplo, los asentamientos en cada tramo son cero.

Las ecuaciones anteriores entonces quedan así:

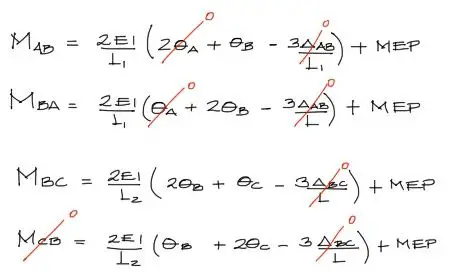
Además, reemplazando numéricamente el resto de los datos del problema:

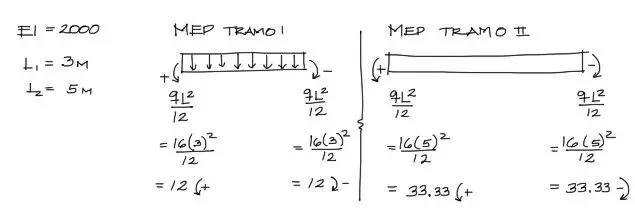
Reemplazando todos los datos en el sistema de ecuaciones:

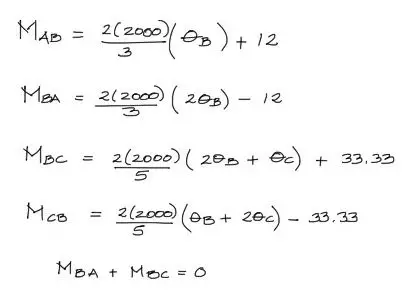
Y si escribimos el sistema de cinco ecuaciones con cinco incógnitas de forma matricial, queda:

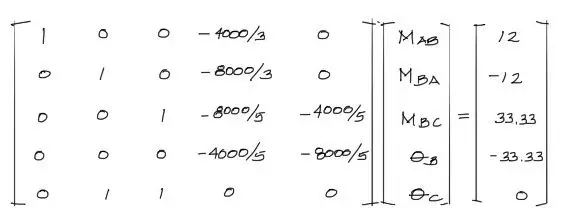
Y resolviendo el sistema, se tiene como resultado:

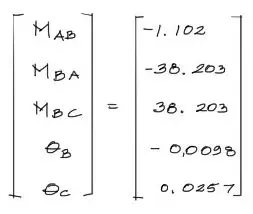
traduciendo estos resultados en forma gráfica para cada tramo de la viga según la convención de signos del método:

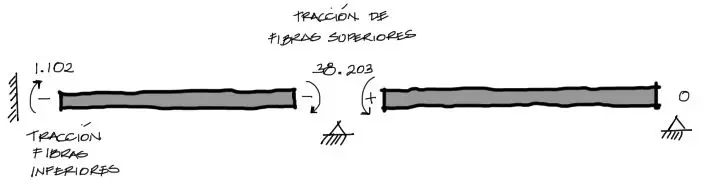
Se debe tener en cuenta que la convención de signos para equilibrar momentos mediante ecuaciones es diferente a la convención de signos utilizada para la graficación de diagramas de momentos flectores. En los diagramas de momentos flectores se utiliza la convención de signos que dicta que los momentos son positivos si la tracción de fibras ocurre en la parte inferior de la viga. Por otro lado si la tracción ocurre en las fibras superiores de la viga el diagrama de momentos en ese punto es positivo. Así entonces:

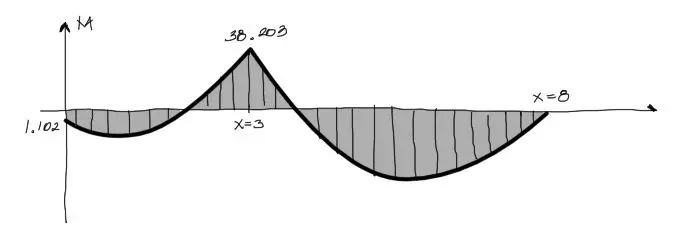
Posteriormente se pueden, a partir de estos resultados, calcular los cortantes, ecuaciones de los diagramas de momento, y puntos máximos de cada tramo. Sin embargo esto se realizará en un siguiente post, sin embargo, puedes averiguar como realizar este cálculo a partir del vídeo Cómo obtener diagramas de M y V a partir de momentos en los extremos.

← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←

autor: Marcelo Pardo