¿Para qué sirven?

Humanos y computadores no resolvemos los problemas matemáticos de la misma manera. La manera de “razonar” de ambos es completamente diferente. Mientras los humanos tenemos capacidad de razonamiento para resolver un problema en específico, el computador es bueno para acciones repetitivas y programables. Aprovechando esta cualidad de los computadores, la forma de resolver problemas matemáticos con éstos es dividiendo dominios e iterando donde a prueba y error, se llegará a la solución buscada.

Los Métodos Clásicos

Cuando se estudia matemática desde la escuela, se aprenden métodos de resolución de ecuaciones, integrales, diferenciación, y sistemas de ecuaciones mediante métodos clásicos, usualmente con reglas de factorización, despeje, integración de variables según la forma de la variable o reemplazo de variables en el caso de sistemas de ecuaciones.

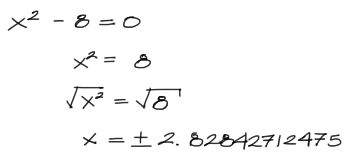
Estos procedimientos son intrínsecos de un razonamiento humano. Sin embargo un computador no puede pensar de esta manera. O si lo hiciera, necesitaría un algoritmo de programación muy avanzado y difícil de programar.

Los Métodos Numéricos

Para encontrar la solución de X en el ejemplo anterior, el computador debe aplicar otro tipo de métodos para encontrar la solución (+-3). El procedimiento que se debe aplicar para resolver esa ecuación corresponde a la de los métodos numéricos, donde por iteraciones sucesivas, se puede encontrar la solución al problema.

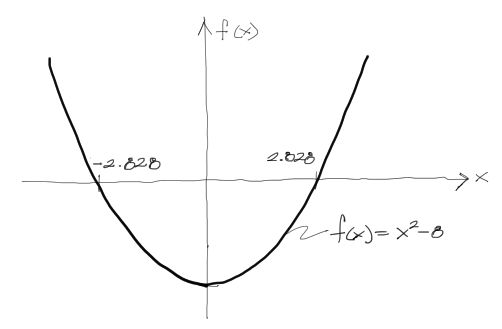
El método de bisección es un método numérico para encontrar el punto donde la función cruza con el eje “X”. Este punto (o estos puntos) son la solución de la ecuación. Gráficamente se ve así:

Para encontrar la solución de esta función (o dicho de otra manera, dónde la función f(x) se hace cero), el computador separará la curva en varios tramos. Luego probará si cada tramo tiene los extremos con el mismo signo, o si los extremos tienen signo cambiado. Si la iteración es hacia la derecha sucede lo siguiente:

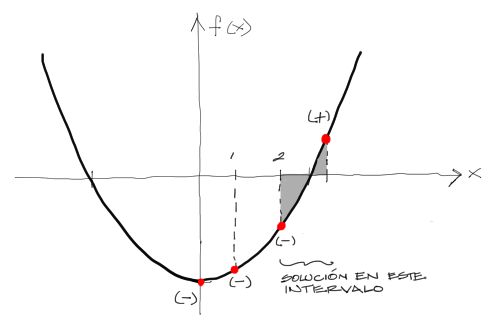
El computador puede hacer divisiones o intérvalos de una unidad hacia la derecha. Luego comprobar si cada uno de los intérvalos tiene en sus extremos f(x) con el mismo signo o diferentes signos. Si cada extremo del intérvalo analizado tiene el mismo signo, la solución no se encuentra en esa dovela. Si los extremos tienen el signo opuesto, la solución está en ese intérvalo (intérvalo sombreado). Como ya se tiene delimitado el intérvalo donde está la solución, se puede subdividir el intérvalo y realizar la misma operación.

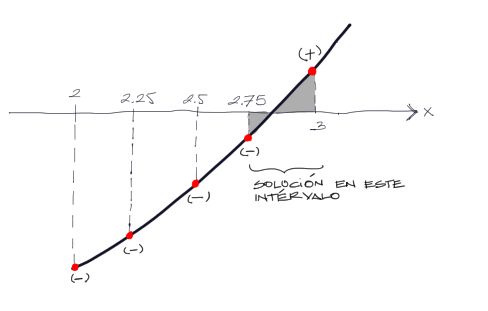
El proceso se repite hasta que el error sea lo suficientemente pequeño como para que ya no sea significativo para propósitos prácticos. De esta manera el computador llegará a una solución muy cercana a 2.82842712475

.

Otro ejemplo gráfico. La integración numérica

La integración en términos prácticos representa la solución de la superficie debajo de una curva.

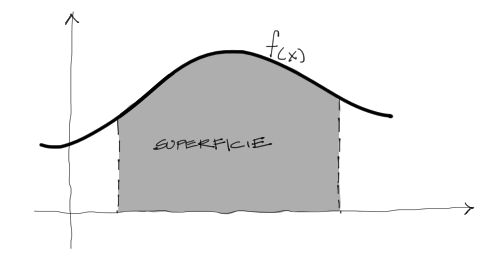
Esta integración puede hacerse por métodos analíticos (cálculo integral) o mediante métodos numéricos. Veremos con un ejemplo ambas resoluciones.

Ejemplo

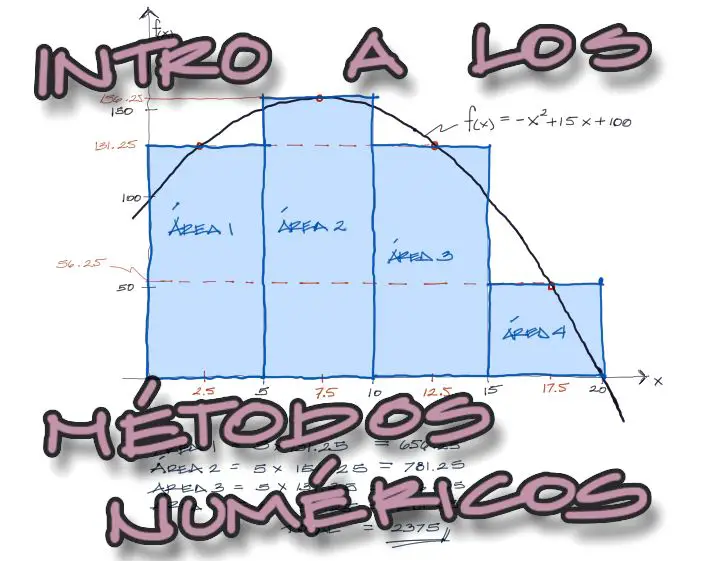
Encontrar el área bajo la curva f(x) = -x^2+15x+100 entre x=0 y x=20. Utilizar el método analítico y el método numérico del punto medio para su resolución.

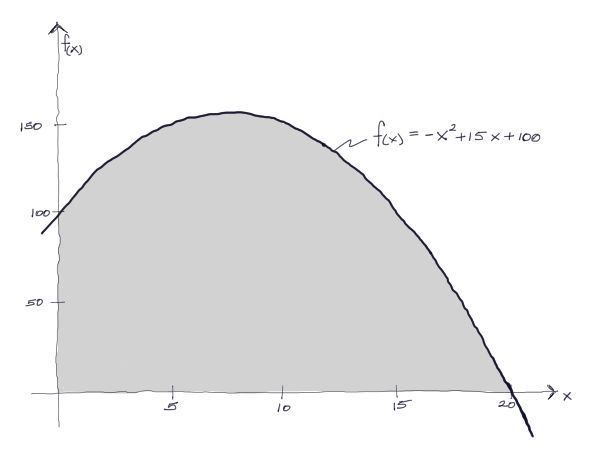
Método analítico (cálculo integral)

La integración de polinomios es relativamente sencilla. Se integra el polinomio y se reemplazan los límites obteniendo así el área bajo la curva:

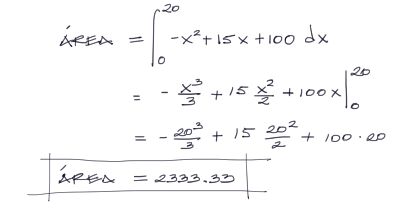
Método numérico del punto medio

Este es uno de los métodos más sencillos de aplicar en la integración numérica de la curva.

Realizar un programa que logre “aprender” todos los métodos de integración analíticamente como en el apartado anterior es una tarea por lo menos difícil. Existe un camino mucho más sencillo de programar.

Podemos encontrar el área aproximada bajo la curva dividiendo el dominio en 4 partes:

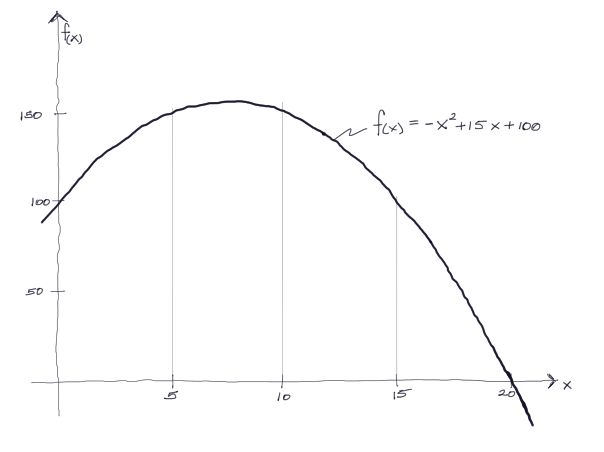
Posteriormente podemos encontrar el punto medio de cada intérvalo. Estos puntos están marcados en rojo en las “X”. De la misma forma, con la fórmula -x2+15x+100 podemos encontrar el correspondiente en “Y” para cada uno de los puntos medios “X”.

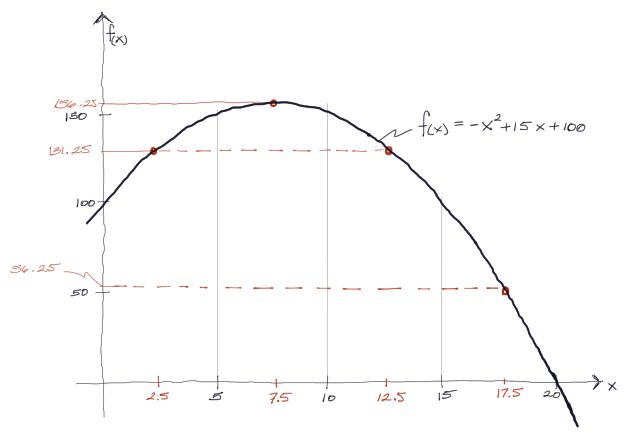
Si imaginamos el área de cada intérvalo como un área rectangular del ancho del intérvalo y de altura media medida al centro del intérvalo, podemos tener una aproximación gruesa del área total sumando todas estas superficies individuales:

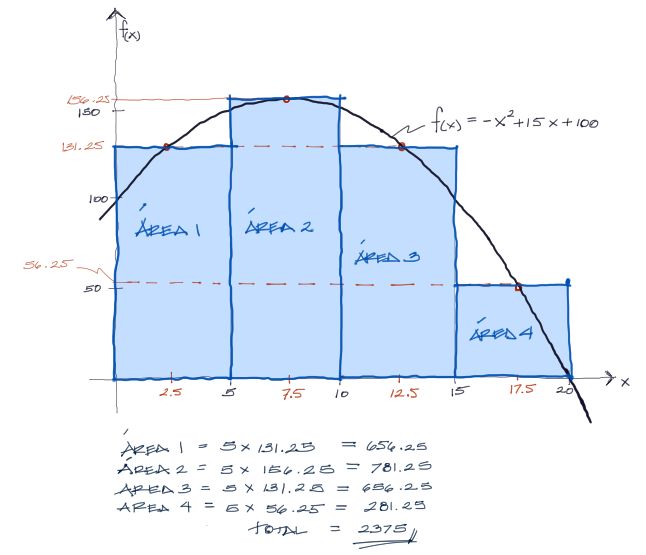
El área aproximada para una 4 divisiones es de 2375. Si se realiaran 500 divisiones (un computador realiza esta tarea con gran facilidad) el resultado ya sería casi exacto.

El código para conseguir dicho resultado en MatLab es:


clc
div = 500
x = linspace(0, 20, div+1)

area_tot = 0
for i = 1:div
disp("-----------")
xi = x(i);
xf = x(i+1);
xm = (xi+xf)/2
ym = -xm^2+15*xm+100
base = xf-xi
area_dov = base*ym
area_tot = area_dov + area_tot
end


Corriendo el código se llega al resultado buscado de Area = 2333.33

Conclusión

Los métodos numéricos en general dividen el dominio del problema en un número finito de partes. Más divisiones en general significan mayor precisión en el resultado obtenido.

Así como existen métodos numéricos de ceros en funciones o de integración, existen métodos numéricos para solución de sistemas de ecuaciones lineales, y resolución de ecuaciones diferenciales.

En la resolución de ecuaciones diferenciales el método numérico más populas es el Método de Elementos Finitos, cuyo proceso en principio funciona de manera similar a la explicada arriba. Sin embargo tiene sus propias complejidades.

Al tomar esta materia en la universidad, muchos estudiantes no entienden el uso práctico de los métodos numéricos, porque no comprenden su aplicación. Se debe entender que todos los programas avanzados de cálculo estructural están elaborados con métodos numéricos. De hecho dichos programas no existirían si no fuera por los métodos numéricos.

Puede parecer frustrante sin embargo, que casi todos los métodos numéricos conocidos ya estén programados en calculadoras y programas de cálculo, dejando al estudiante solo el conocimiento teórico de estos métodos. De todas maneras es bueno conocerlos a profundidad para saber qué procesos de cálculo se llevan a cabo en el cálculo de estructuras con Software Especializado. …Y quien sabe, en algún momento realizar un Software propio que reemplace los paquetes estructurales que se hacen prohibitivos económicamente.

Video

El artículo en vídeo de Youtube es el siguiente:

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←