Planteamiento del problema

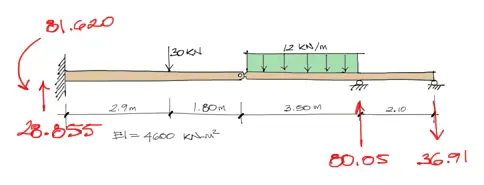
Se plantea resolver la siguiente viga

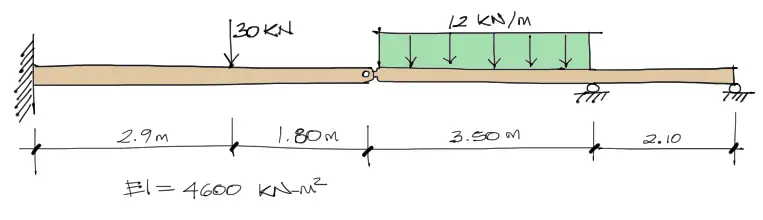
Se puede observar que la viga cuenta con una articulación en centro. Esto por definición es algo más complicado de resolver por métodos tradicionales.

método de resolución

La viga se resolverá a través del método matricial de rigidez.

Se sabe típicamente que cada elemento de barra cuenta con una matriz de rigidez. En el caso de vigas, cada elemento cuenta con una matriz de rigidez de dimensiones 4×4. Esto es a raiz de que el elemento tiene 2 nudos, y cada nudo cuenta con dos grados de libertad. En total 4 grados de libertad. Esta matriz se la puede entender en el enlace: Matriz de rigidez de viga.

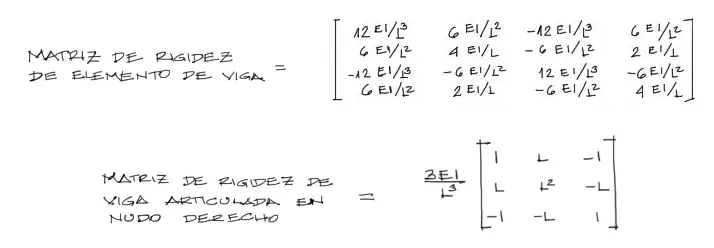
Sin embargo cuando la viga cuenta con articulaciones, la cosa cambia. Se debe modificar la matriz de rigidez para anular el grado de libertad de giro en el nudo que tiene la articulación. La manera de hacer esto se encuentra en: Matriz de rigidez de elemento de viga articulado.

Numeración de grados de libertad y elementos

Asignando la numeración de grados de libertad y elementos de izquierda a derecha:

Notemos que el grado de libertad de giro para el elemento 2, nudo derecho, no existe. Esto se debe a que se está asignando una matriz de rigidez articulada en nudo derecho para el elemento 2.

Para crear la articulación basta con asignar la articulación a uno de los dos elementos (2 o 3). Se puede asignar de igual forma un nudo articulado tanto al elemento 2 como al 3 simultaneamente. Sin embargo en este ejercicio se asignará la articulación solo al elemento 2.

Matrices de rigidez

La fórmula de matriz de rigidez que adoptaremos para los elementos 1, 3 y 4 será la matriz de 4×4. Para el elemento 2 adoptamos la matriz articulada con 3 grados de libertad, de 3×3.

Aplicando las fórmulas de matriz de rigidez para cada elemento tenemos:

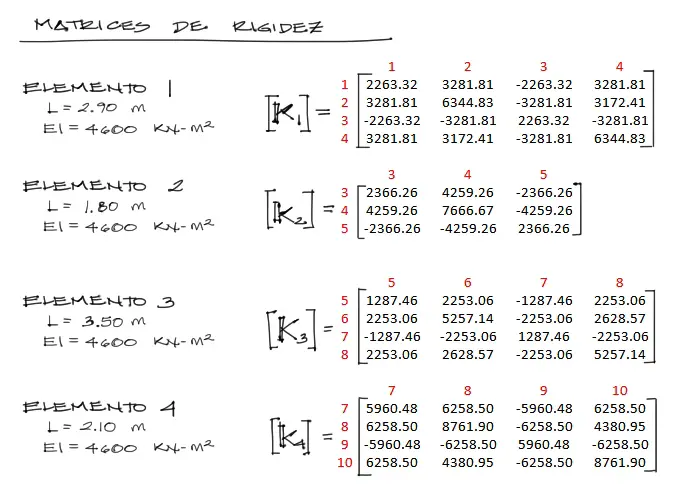
Se debe prestar especial atención en la numeración de nudos. Esta numeración corresponde a los grados de libertad de cada elemento. El elemento 2 por ejemplo, no cuenta con el grado de libertad 6.

Ensamblaje de la matriz de rigidez

Una vez numerados los grados de libertad de cada matriz de rigidez, transportamos cada uno de los elementos dentro de la matriz de rigidez global.

Si dos elementos de las matrices de rigidez de cada barra caen dentro de una misma casilla dentro de la matriz de rigidez de toda la estructura, se suman.

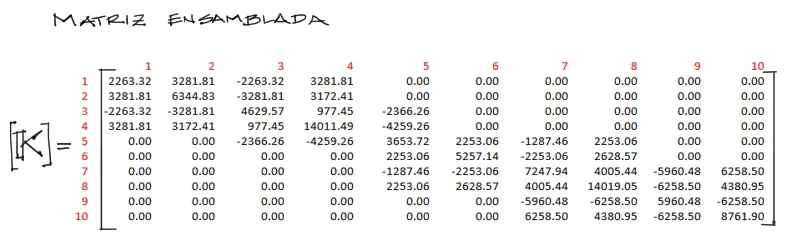
Creación del vector de cargas distribuidas

Las cargas distribuidas deben convertirse en cargas puntuales equivalentes hacia los nudos antes de cargarla en la estructura. Esta transformación se logra a partir de conceptos de Momento de Empotramiento Perfecto.

Para el caso de cargas distribuidas uniformes, aplicamos:

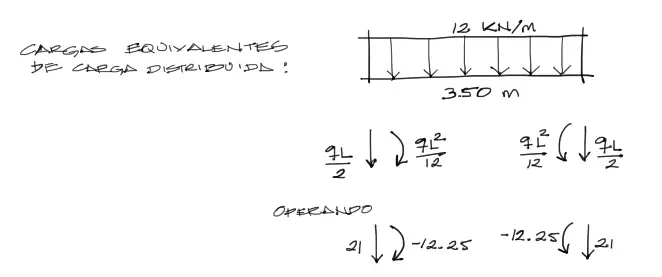
El elemento sobre el que se aplica la carga es sobre el elemento 3, con grados de libertad 5, 6, 7 ,8. Por tanto las fuerzas equivalentes deben transportarse en orden: fuerza, momento, fuerza, momento, dentro del vector de cargas de toda la estructura:

Cargas puntuales y reacciones

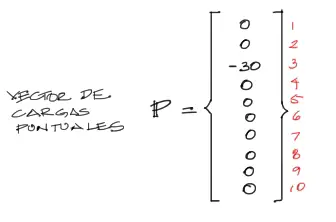
Las cargas puntuales de la viga se aplican directamente sobre un vector de cargas de la estructura sin ninguna transformación necesaria. En este caso existe una carga de 30 KN aplicada en el grado de libertad 3, en el sentido opuesto al positivo. Entonces:

De la misma manera creamos un vector de reacciones con las incógnitas de reacción en los grados de libertad restringidos. Existen apoyos en los grados de libertad 1, 2, 7, 9:

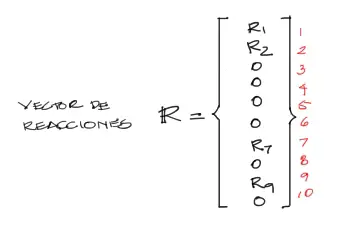
Resolución del sistema de ecuaciones

Se ha formado por fin un sistema de ecuaciones de la siguiente forma:

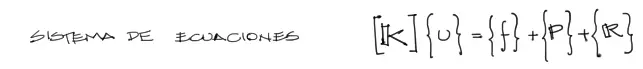
Este es un sistema de 10 ecuaciones con 10 incógnitas. De todas estas ecuaciones debemos anular las ecuaciones restringidas por los apoyos. En este caso anulamos filas y columnas 1, 2, 7, 9 del sistema de ecuaciones y nos queda:

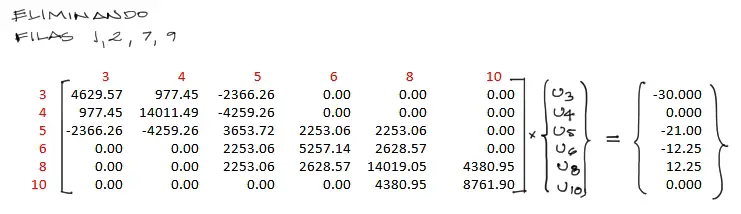
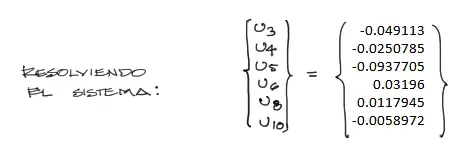
Se resuelve el sistema donde las incógnitas son los desplazamientos.

Reacciones de la viga

Encontrados los desplazamientos del sistema, podemos reescribir el sistema de ecuaciones completo ya con los desplazamientos encontrados. El sistema queda así:

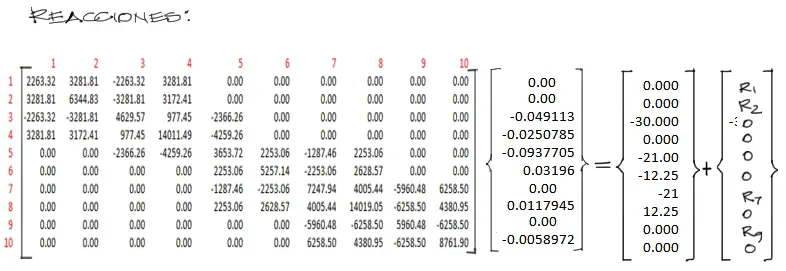
Para encontrar las incógnitas R1, R2, R7, R9 del sistema mostrado, solo se debe despejar el vector, llevando las cargas al lado izquierdo de la ecuación. Además se calcula la multiplicación de [K]·{u} y se restan las fuerzas. Queda:

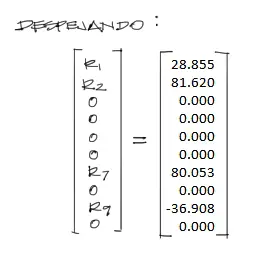
De forma gráfica:

Qué sigue?

Luego se deben encontrar los diagramas de cortante y momento para la viga. Este proceso lo dejo para el siguiente artículo en el enlace:
Solicitaciones en viga articulada por el método de rigidez.

autor: Marcelo Pardo