El problema
En el anterior artículo habiamos visto como calcular la matriz de rigidez de un elemento de barra en el espacio tridimensional. El enlace a ese artículo es Matriz de rigidez de pórtico en 3D – coordenadas globales.
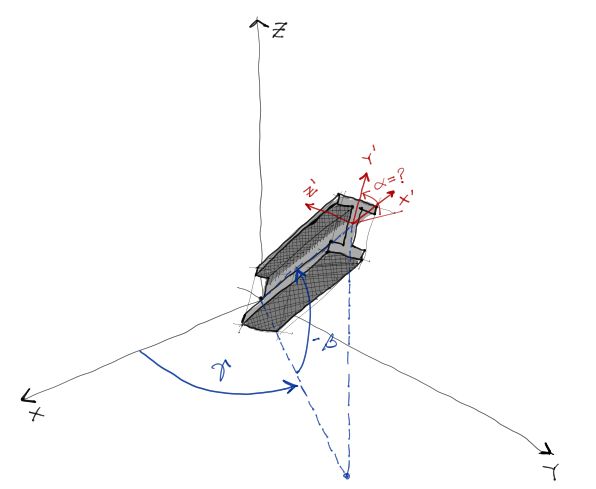
El problema se presenta al momento de programar el algoritmo para encontrar los ángulos “alfa”, “beta” y “gamma”. Se debe buscar la manera de que estos ángulos se calculen automáticamente, solo introduciendo las coordenadas de los extremos. Sin embargo esta tarea no es tan sencilla pues si bien “beta” y “gamma” se pueden encontrar automáticamente, la rotación sobre el eje del elemento debe ser introducida por el usuario.
Este es el caso del programa OpenSees por ejemplo, donde en función a la orientación del elemento, se debe indicar la dirección en la que apunta el eje principal de la barra.
La manera de ingresar este dato en OpenSees es sin embargo, demasiado incómoda y anti intuitiva, especialmente cuando la barra está inclinada, ya que en esta situación es difícil saber la dirección en la que apunta el eje local Y’ respecto a los ejes globales. Es mejor dejar que el programa asuma un ángulo de rotación de la barra sobre su eje que sea estandar. Y si se desea cambiar esto en algún momento, se lo haga manualmente.
El algoritmo
Ángulo Alfa
Sabemos que toda barra cuyos 3 ángulos alfa, beta y gamma son cero, es una barra orientada como en el gráfico:
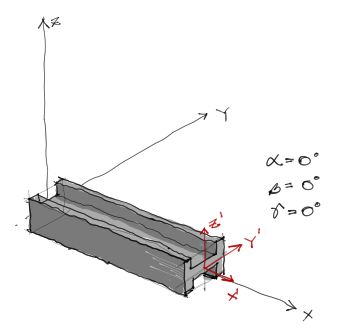
…con los ejes locales X’, Y’, Z’ orientados en la misma dirección que los ejes globales XYZ. Sin embargo también sabemos que la posición natural de una viga está rotada 90° respecto a su eje X’. Por tanto asumiremos un ángulo “alfa” estandar de 90° para absolutamente todos los elementos, sean estos vigas, columnas, o elementos inclinados.
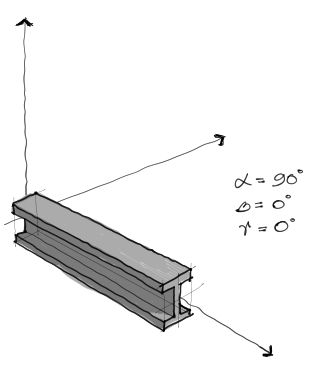
Obviamente al momento de realizar el programa de cálculo, se permitirá cambiar este ángulo en caso de que el usuario lo quisiera. Sin embargo si no se introducen datos sobre la rotación “alfa”, por defecto se asume alfa = 90°.
álgulo beta y gamma
Asumamos ahora que la barra estudiada está en cualquier posición sobre el espacio XYZ. Sabemos ya que el eje local Y’ estará apuntando hacia arriba en todo momento (salvo casos excepcionales cuando la barra esté completamente vertical. Este caso se verá más adelante).
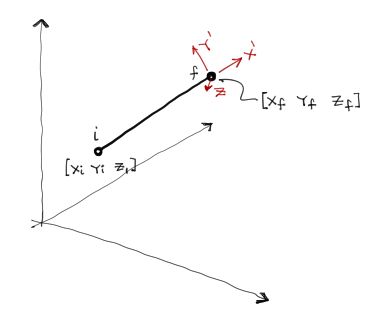
En la imagen “i” representa nudo inicial y “f” nudo final, indicando que la dirección de la barra (sus ángulos) se mide desde el nudo “i”.
A partir de esta posición general, podemos obtener “beta” y “gamma” de la siguiente manera:
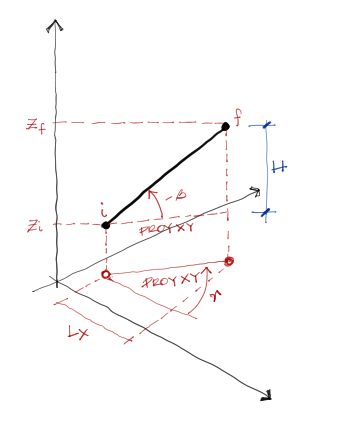
el ángulo “beta” que es negativo hacia arriba, lo obtenemos por trigonometría, usando la hipotenusa (Longitud de la barra) y el cateto opuesto del triángulo de la imagen “H”. entonces:
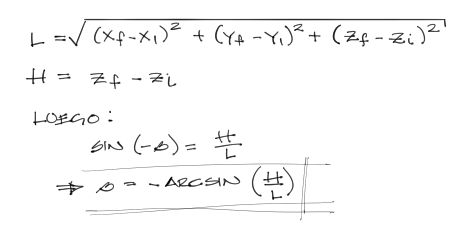
La longitud L siempre será positiva. H será positivo cuando la barra ascienda y negativo en caso contrario. Por tanto el cálculo de beta devuelve tanto la magnitud del ángulo como el signo de dirección de la barra.
Para el cálculo de “gamma” debemos calcular tanto la proyección de la barra sobre el plano XY como la longitud Lx. para esto:

Deben implementarse dos condicionantes al momento de programar el cálculo de “gamma”. Si la barra es completamente vertical, no tiene sentido tomar en cuenta el ángulo gamma de rotación, que generaría una doble rotación de la barra sobre su eje. Por tanto si la barra es completamente vertical, la rotación de la barra se controlará solo mediante “alfa”.
La segunda condicionante consiste en determinar si el ángulo “gamma” es metido en sentido horario o antihorario. Eso solo puede ser detectado a partir de (Yf-Yi). Si este valor es negativo, el ángulo “gamma” se mide en sentido horario.
programación
Con estos pasos ya explicados, la implementación del algoritmo en cualquier lenguaje de programación es inmediata. Para el manejo de matrices como esta, lenguajes de programación como matlab u Octave ya solo sirven para propósitos didácticos, ya que su procesamienteo comienza a sentirse lento al momento de correr. Es más adecuado el manejo de un lenguaje de programación que permita la compilación para tener más rapidez en los cálculos.
autor: Marcelo Pardo