
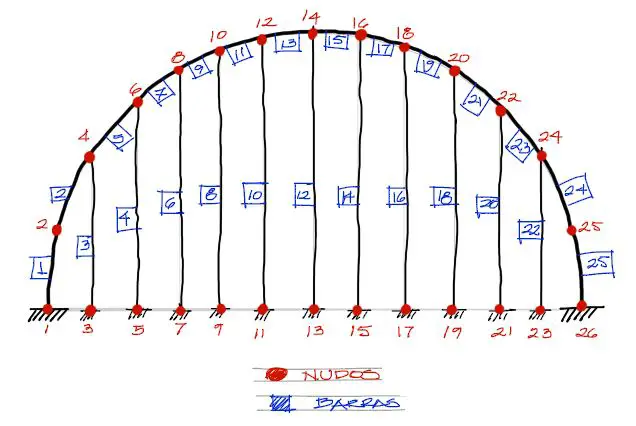
Pasos previos
En anteriores publicaciones elaboré la matriz de rigidez de cada elemento del pórtico en 3d a analizarse y además el ensamblaje de la matriz de rigidez de toda la estructura.
Los enlaces a esas publicaciones están en:
– Ejemplo de resolución de Portico en 3D por elementos finitos – Voladizo circular
Ejemplo de Portico en 3D por el método de rigidez o elementos finitos – Voladizo circular – PARTE 2.
Habiendo calculado ya las matrices de rigidez elementales y la de toda la estructura, toca calcular las cargas equivalentes en los nudos a partir de las cargas que llegan a cada vigueta.
Cálculo de cargas en viguetas
Sabemos por conceptos de estructuras, que los primeros elementos que soportan las cargas de uso de la estructura son las viguetas junto con la carpeta de compresión, y estas viguetas son las que posteriormente transmiten la carga a las vigas principales y estas últimas luego a las columnas.
Como en nuestro caso estamos modelando tanto viguetas como vigas, no necesitamos calcular la carga sobre la viga curva sino sobre las viguetas (exceptuando la carga muerta por peso propio de la propia viga).
Carga muerta por peso propio
La carga muerta por el peso propio de la losa que llega a cada vigueta es la sección transversal de un ancho de influencia de 50cm multiplicada por el peso específico del concreto.
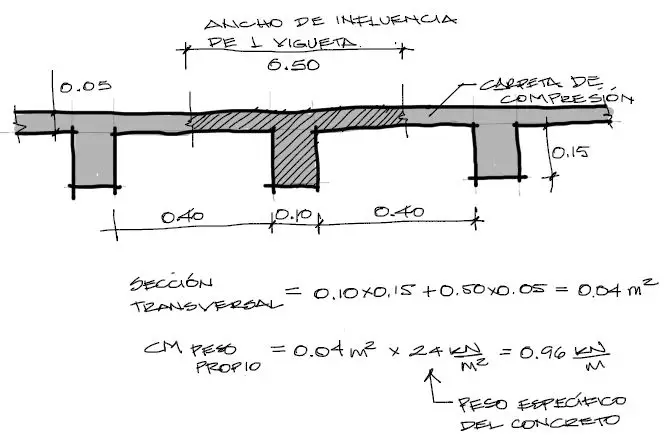
Para el peso propio de la viga se procede de manera similar. 0.25*0.50*24=3KN/m
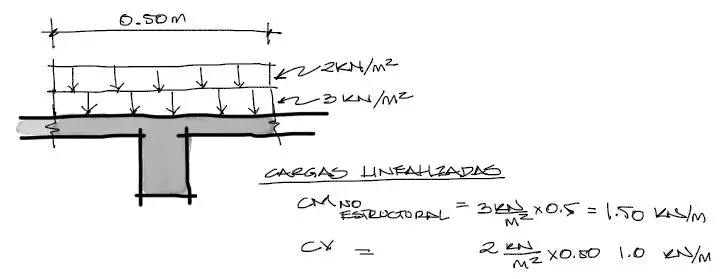
Carga muerta no estructural y carga viva
Un proceso similar se aplica a la carga muerta no estructural y a la carga viva. La carga muerta no estructural que suele llegar a una vigueta suele estar entre 2 y 4 KN/m2. En este caso aplicaremos una carga promedio muerta de 3KN/m2 y una carga viva de 2KN/m2 correspondiente a uso de viviendas. Se tiene entonces:
Mayoración de cargas
La manera correcta de cargar estructuras es a partir de la mayoración de cargas. La ACI indica que la carga muerta se mayora por un factor de 1.2 y la viva por 1.6. Entonces se tiene:
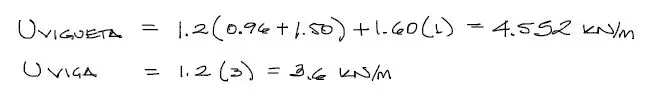
La carga calculada sobre los elementos estructurales se ve más o menos de la siguiente manera:
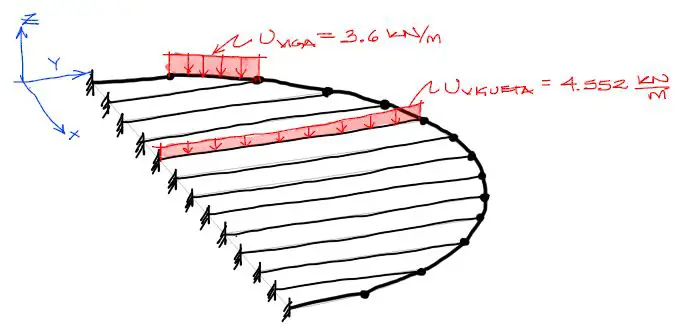
Carga puntual equivalente en nudos
Cada viga o vigueta cuenta con una carga distribuida aplicada a lo largo de su longitud. Esta carga para aplicarse al cálculo por rigidez, debe concentrarse en los nudos. En otras palabras, solo los nudos son capaces de resistir carga. Por tanto debemos encontrar cargas equivalentes en los nudos iguales al efecto que produciría la carga equivalente sobre los mismos nudos.
Para eso aplicamos el concepto de momentos de empotramiento perfecto. Para cada tramo de longitud L y de carga q, existe una carga y momento equivalente en los nudos a partir de la carga distribuida:
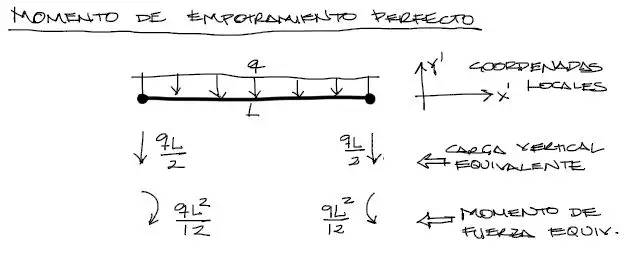
Debemos notar que las cargas se aplican sobre los ejes locales de la viga y luego se debe hacer la transformación correspondiente para llevar las cargas encontradas a coordenadas globales bajo el mismo procedimiento aplicado a las matrices de rigidez de cada elemento.
Por ejemplo para el tramo de viga 7…
Nuestro elemento estrella de ejemplo se analizará transformando la carga distribuida a cargas equivalentes en los nudos. En este caso se tiene un tramo de viga muy corto sometido a peso propio. entonces:
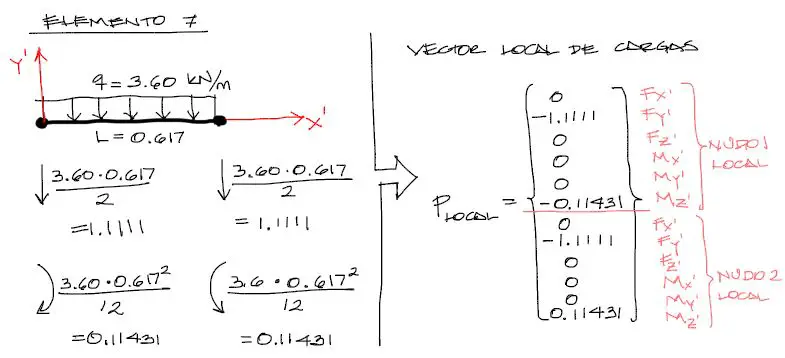
El cálculo de las cargas verticales y momentos de fuerza en los nudos es inmediata, como se ve en la figura. Luego estas cargas deben trasladarse a un vector local de dimensión 12×1. A la vez, al momento de trasladar las fuerzas equivalentes al vector, debemos tener cuidado con la posición y signo de las fuerzas calculadas sobre el vector.
Como se ve, las fuerzas verticales apuntan hacia abajo respecto a la dirección Y’ local, por tanto deberán ser negativas.
Respecto a los momentos de fuerza, estos momentos giran al rededor del eje Z’ que se dirije perpendicular al plano de análisis hacia nosotros. El signo del giro es antihoriario positivo y horario negativo (por la regla de la mano derecha) por tanto, el momento del nudo izquierdo es negativo y el momento derecho positivo. Todo esto se ve reflejado en el vector de la derecha.
Posteriormente transformamos este vector de carga según las reglas de transformación mencionadas en Rotación de coordenadas locales a globales de matriz de rigidez de pórtico. Sin embargo en este caso para la transformación de vectores de carga, se debe solo multiplicar la matriz transpuesta de transformación [T] por el vector de carga {P_local}. Se repite el proceso para la rotación respecto al eje, rotación en la base, y rotación en altura. Entonces:

El vector resultante después de todas las transformaciones es:
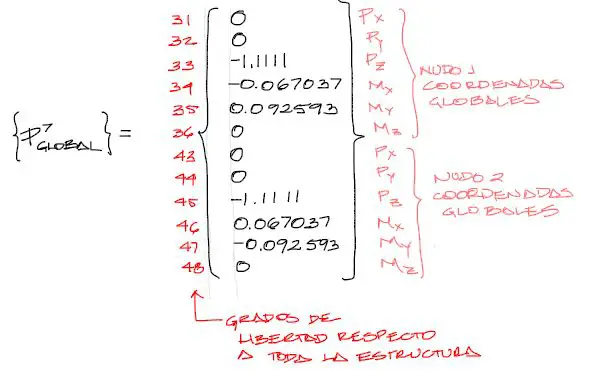
Finalmente se deben trasladar todas las componentes del vector de fuerzas del elemento 7 a un vector de fuerzas de toda la estructura, según los grados de libertad que corresponden al elemento 7 dentro del vector global de dimensión 156×1. Obviamente, igual que con el ensamblaje de matrices de rigidez, si los valores del elemento 7 se traslapan con valores de otros elementos, los valores dentro del vector de cargas {P} de toda la estructura se suman
Vector de cargas de toda la estructura.
Si gustas descargar el vector de cargas de toda la estructura, el enlace de descarga es:
VectorCargas.zip
¿Qué sigue?
Hasta acá ya la matriz de rigidez y el vector de fuerzas de la estructura. Sigue eliminar grados de libertad de los nudos restringidos (apoyos) y la resolución del sistema de ecuaciones. esto se dejará para la siguiente publicación.
autor: Marcelo Pardo


Muy bueno….
Gracias ing Marcelo por el aporté
Muchas gracias Carlos por tu comentario!