Planteamiento del problema
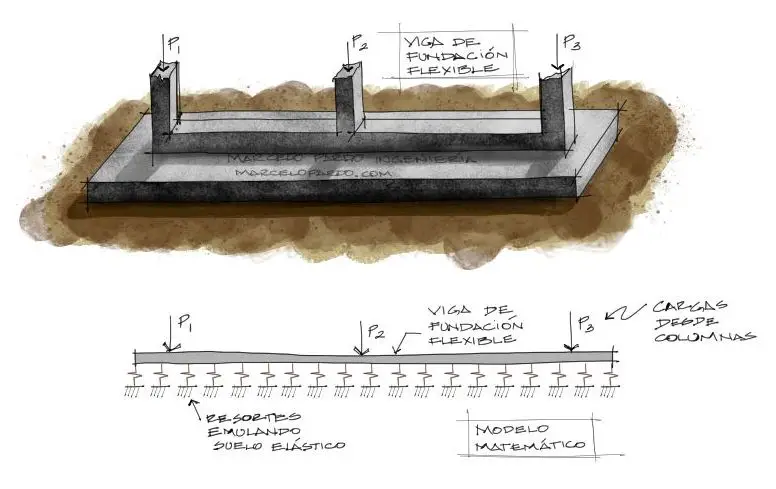
En muchas situaciones de interacción suelo – estructura, es necesario modelar estructuras apoyadas sobre lecho elástico. Este es el caso de vigas de cimentación o losas de cimentación, donde la deformación de la fundación en la interacción con el suelo es imprescindible para conocer los esfuerzos a los que estará sometida dicha fundación. Esta es la situación donde para emular suelo, se utilizan resortes en la base de las estructuras, como en la imagen que se muestra a continuación.
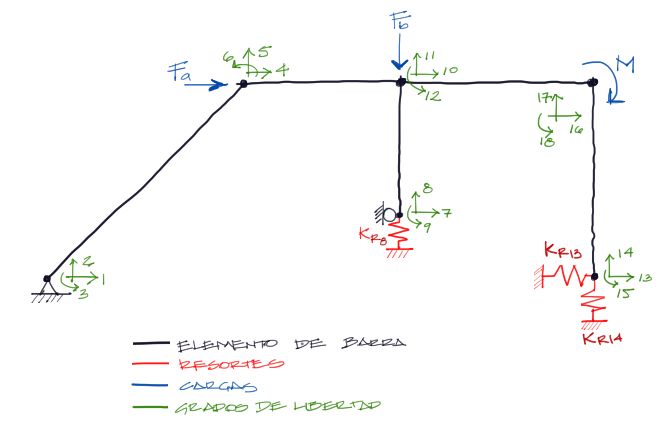
Sin embargo, para la explicación de la implementación de resortes en un modelo de elementos finitos utilizaremos un modelo más completo, con cargas verticales y horizontales. El pórtico de ejemplo será el siguiente:
El sistema de ecuaciones
El sistema anterior cuenta con 18 grados de libertad, por lo que el sistema de ecuaciones conformado será de una matriz de rigidez de 18×18 elementos y por tanto 18 desplazamientos (12 desplazamientos y 6 rotaciones).
El sistema conformado genéricamente se ve más o menos así:

Si reemplazamos todos los datos conocidos del problema en particular (exceptuando los resortes), se tiene lo siguiente:
Los coeficientes Kij de la matriz de rigidez se calculan según la teoría de matrices de rigidez y de ensamblaje de matrices según publicaciones anteriores.
– Los desplazamientos que se anulan o toman valor cero por los apoyos son U1, U2 y U7. El resto de los desplazamientos permanecen como incógnitas.
– Las fuerzas aplicadas F1, F2, M se aplican en los grados de libertad 4, 11 y 18 respectivamente. El resto de las fuerzas F del vector de fuerzas toman valor cero.
– Las reacciones desconocidas del problema corresponden a los grados de libertad restringidos. O sea, R1, R2 y R7. El resto de las reacciones son nulas.
Con todo esto en cuenta, queda el siguiente sistema de ecuaciones de la estructura:

Inclusión de resortes
Hasta el momento al sistema de ecuaciones no se han colocado los apoyos de resorte. Para entender como incluirlos, debemos enfocarnos en un apoyo cualquiera y analizar las deformaciones.
Si analizando un nudo en particular perteneciente a la intersección entre dos elementos de pórtico, y nosotros analizamos sus deformaciones y el nudo se desplaza, por ejemplo, hacia arriba:
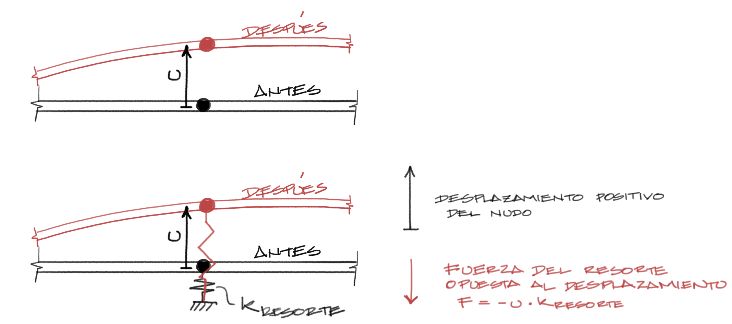
El nudo sin el resorte experimenta un desplazamiento vertical hacia arriba positivo. Si a este mismo nudo se le aplica un resorte vertical, el resorte se estira, y este estiramiento produce una fuerza vertical negativa opuesta al desplazamiento del nudo. Si el módulo de deformación del resorte es K_resorte, entonces la fuerza que se opone al movimiento será F = -u*K_resorte.
Esta fuerza que se opone al desplazamiento deberá sumarse a las fuerzas aplicadas externas a la estructura. Para cada resorte de la estructura entonces, se tiene:
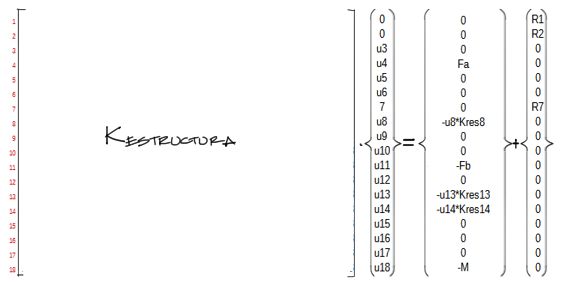
Se implementan las fuerzas de resortes en los grados de libertad 8, 13, 14 que son los grados de libertad donde en el ejemplo se muestran los resortes. Asumiremos que los módulos elásticos de los resortes son Kres8, Kres13 y Kres14 respectivamente.
Al implementar las fuerzas de resorte al lado derecho de la ecuación surge el inconveniente de tener desplazamientos a los dos lados del sistema de ecuaciones. El sistema de ecuaciones escrito de esta manera no puede ser resuelto, y se deben reagrupar las incógnitas hacia la izquierda del sistema de ecuaciones.
Para lograr esto último, nos concentramos en una sola fila del sistema de ecuaciones. En esta fila (la fila 8 para nuestro ejemplo) reescribimos la ecuación del sistema de ecuaciones.
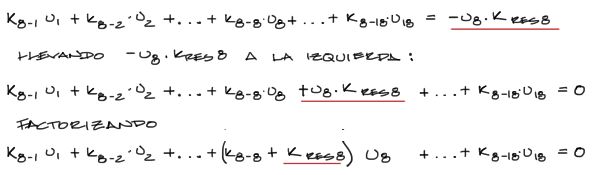
El proceso mostrado en la figura consiste en multiplicar la matriz de rigidez por los desplazamientos, de tal forma que convirtamos el arreglo matricial de vuelta hacia una nomenclatura de ecuaciones ordinarias. Posteriormente trasladamos el término -u8*Kres8 hacia el lado izquierdo de la ecuación, y luego factorizando términos iguales (en este caso u8) terminamos con K8-8 de la matriz de rigidez sumada a Kres8 del resorte.
En resumen, cada que coloquemos un resorte en un grado de libertad, eso equivale a sumar el módulo elástico del resorte al elemento de la diagonal principal de la matriz de rigidez en el grado de libertad donde se acomode el resorte.
En el ejemplo del pórtico arriba, se tienen resortes en los grados de libertad 8, 13 y 14, por tanto Kr8, Kr13 y Kr14 se acomodarán en la diagonal principal en la matriz de rigidez de toda la estructura, de la manera siguiente:

A partir de este punto, la resolución de la estructura sigue el curso regular explicado en otros artículos.
Fuerza resultante en los resortes
Una vez encontrados los desplazamientos en los nudos no restringidos, es natural querer encontrar las reacciones en los resortes. Para lograr esto solo se debe multiplicar el desplazamiento del grado de libertad del resorte por el módulo elástico del resorte, pero con el signo cambiado, pues el resorte se opone al movimiento del nudo. O sea:
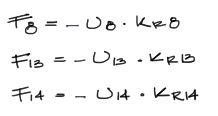
El resto de las reacciones de apoyos convencionales se encuentran de la manera tradicional.
Ejemplo
He desarrollado en vídeo un ejemplo de la manera como se resuelve una estructura concreta con apoyos de resortes en el siguiente enlace:
El vídeo está restringido para miembos del canal, sin embargo puedes volverte miembro por tan solo 2 $us mensuales. Te aseguro que valdrá la pena.
autor: Marcelo Pardo

