Video
Este ejercicio ha sido resuelto en vídeo en el enlace siguiente:
Enunciado
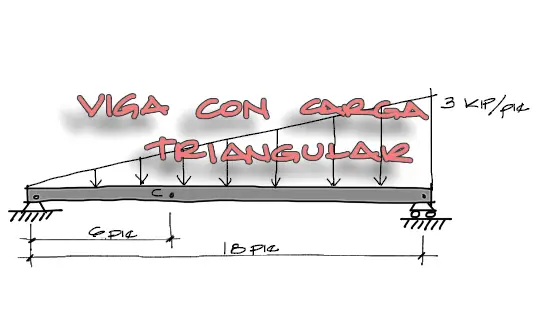
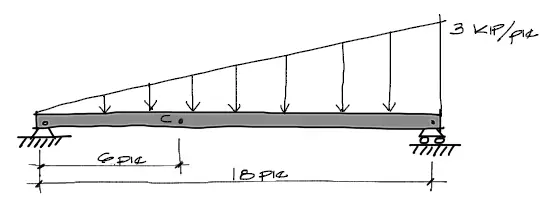
Se pide encontrar las solicitaciones internas en el punto C de la viga mostrada en la siguiente imagen
Resolución
Resultante de fuerzas distribuidas
El primer paso en la resolución por métodos clásicos de cualquier viga consiste en equilibrar externamente la estructura. Esto equivale a encontrar sus reacciones.
Antes de encontrar las reacciones, debemos encontrar la resultante de las cargas distribuidas y su posición respecto al origen escogido. En este caso tenemos:
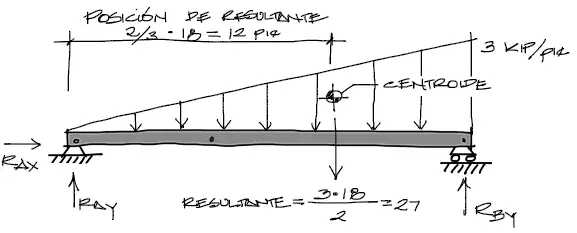
La resultante de una carga distribuida triangular es la “superficie” bajo esta curva. o sea, base·altura/2 y la posición de la resultante está a 2/3 de la base medida desde su esquina opuesta a la esquina a 90°.
Equilibrio externo
Ahora si procedemos al equilibrio externo a partir de las tres ecuaciones de la estática. El pivote para la suma de momentos puede ser cualquier punto pero escogemos la esquina izquierda por convención.

Por álgebra se encuentran las variables Rax, Ray, Rby.
Resultante de fuerzas de la viga cortada
El enunciado pide las solicitaciones en el punto C. Por tanto hacemos un corte imaginario en este punto y equilibramos cualquiera de los dos lados del corte de la viga. Por comodidad y facilidad escogemos el lado izquierdo. El lado derecho forma un trapecio con la carga distribuida y el proceso se hace un poco más tedioso en ese caso.
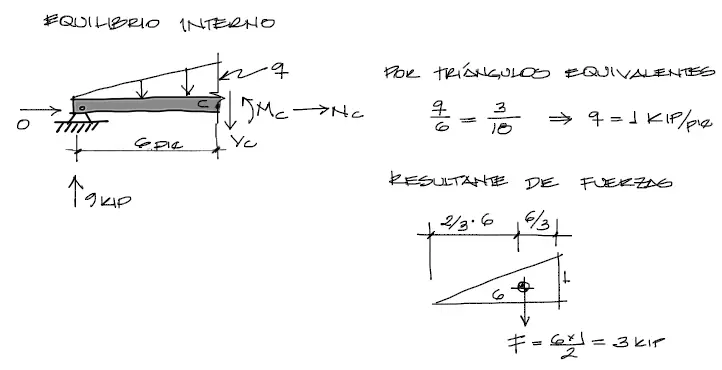
Entonces, antes de equilibrar el corte del diagrama de cuerpo libre, debemos encontrar las resultantes de las fuerzas actuantes. En este caso la carga triangular truncada ya no tiene la altura de 3 kip/pie al borde derecho. La altura q desconocida de la carga se puede solucionar a partir de relaciones de triangulos con la carga más grande.
Una vez encontrada la altura de q, ya se puede proceder a encontrar la resultante de la carga triangular a la izquierda del corte y también su posición respecto de los extremos.
Equilibrio interno
Luego, al igual que en el equilibrio externo, aplicamos las 3 ecuaciones de equilibrio al corte en C, y resolvemos.
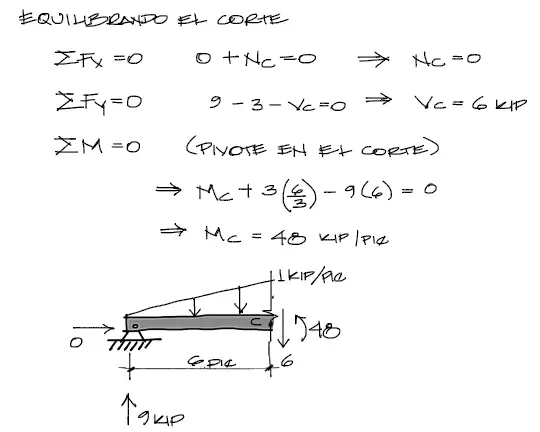
En este caso, la suma de momentos se suele efectuar con pivote en el corte. Esto trae beneficios ya que la variabe Vc no entra dentro de las ecuaciones de momento, y así solo tenemos una incógnita por cada ecuación.
Resolviendo las 3 ecuaciones encontramos las solicitaciones internas de Vc y Mc en la viga.
autor: Marcelo Pardo

Muchas gracias por el valioso aporte, la excelente pedagogía y por todo el.tiempo, trabajo y recursos invertidos….
Un saludo Sergio! muchas gracias por comentar