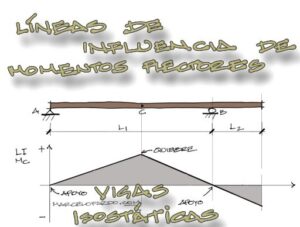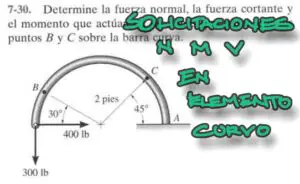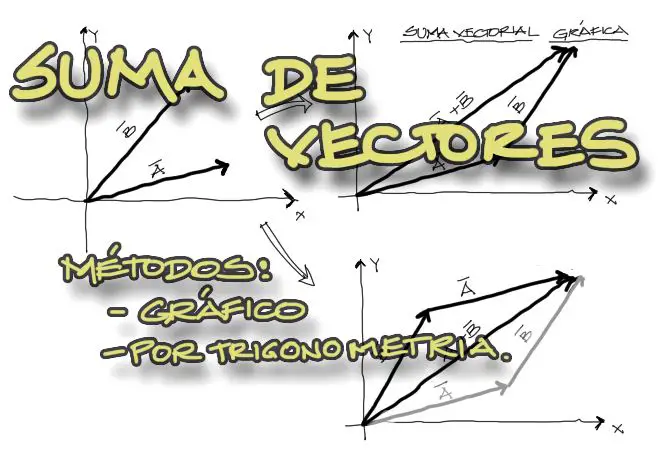
Las fuerzas son vectores
Las fuerzas son expresiones matemáticas con un significado físico. Ya que las fuerzas necesitan expresar tanto la magnitud como la dirección y en la cual está siendo aplicada la fuerza, las fuerzas se expresan a partir de vectores.
Estos vectores pueden expresarse en dos o en tres dimensiones (también en una sola dirección pero no es común esto último).
Cuando los vectores se expresan en un plano cartesiano XY, suelen expresarse de dos maneras: Mediante magnitud dirección y sentido o mediante componentes:
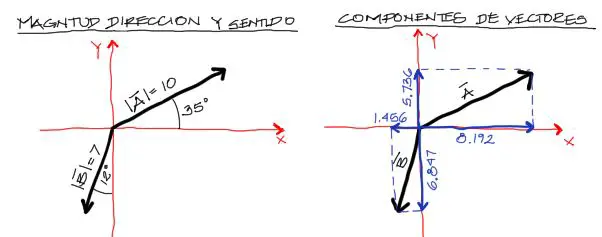
A simple vista la notación izquierda parece más práctica que la de la derecha pero como se verá más adelante, la derecha es mucho más fácil de manejar a la larga.
Suma de vectores Gráficamente
Cuando se realiza la suma de vectores, la manera más simple de visualizar la suma entre dos vectores es acomodando un arreglo punta cola entre los dos vectores a sumar. No importa cual vector se coloca antes y cual después, ya que la suma de vectores es conmutativa. El vector resultante será entonces un vector que coincida con la cola del primer vector y la punta del segundo vector. Entonces para los vectores A y B, la suma queda de la siguiente manera:
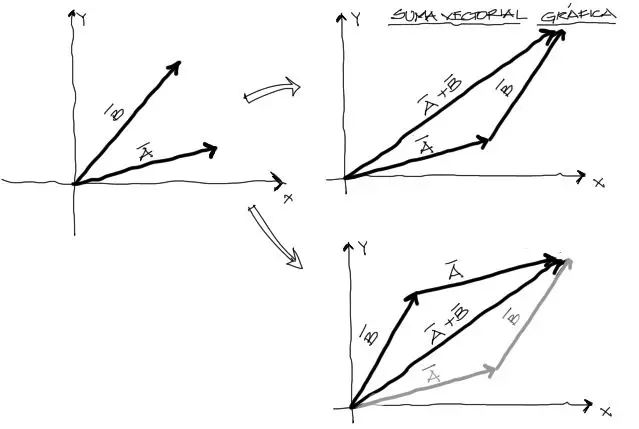
Como se puede ver, no importa el orden en el cual acomodamos los vectores “punta-cola” a sumar, el resultado de A+B será siempre el mismo.
Otro método para lograr la suma de vectores es trazando paralelas de las direcciones de los vectores A y B como se muestra en la gráfica. El punto donde intersectan ambas paralelas corresponde al extremo de la “cabeza” del vector suma A+B. el vector suma A+B arranca en el origen de los vectores A y B.
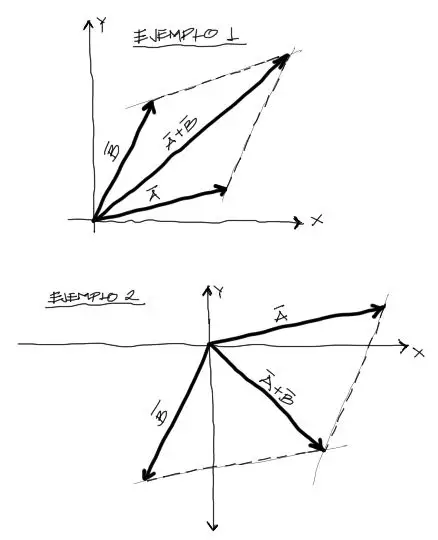
Si bien la suma gráfica nos otorga una persepción sencilla del método de suma de vectores, no es práctica en términos de conocer la magnitud o dirección real del vector sumado A+B ya que está sujeto a errores de visualización y de medición de los ángulos y distancias.
Suma de vectores mediante ley de cosenos
Cuando aplicamos la suma de vectores a través del método gráfico descrito, se forman triángulos de todo tipo y proporciones.
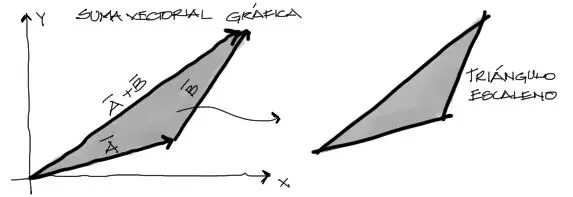
Los triángulos que se forman a partir de la suma de vectores generalmente son escalenos (todos los lados de diferente magnitud). Al generarse triángulos de proporciones que no forman ningún ángulo recto, la relación entre ángulos y lados de un triángulo está regida por dos leyes: Ley de Senos y Ley de cosenos.
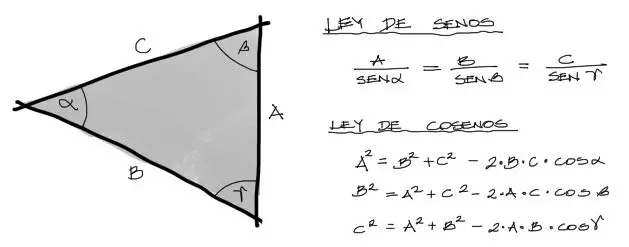
A partir de estas leyes, dependiendo de los datos que se tengan del problema, se pueden encontrar los datos faltantes ya sea aplicando ley de senos o ley de cosenos.
Ejemplo
– Resultante de fuerzas por ley de cosenos
Autor: Marcelo Pardo