Enunciado
Se pide encontrar las ecuaciones de solicitaciones de la viga hiperestática de un tramo mostrada en la figura.
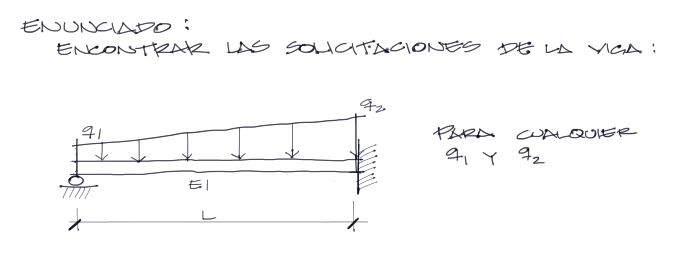
La rigidez es constante, EI, y la longitud de la viga L. Se supone que la carga distribuida es trapezoidal de valores literales q1 y q2 cualesquiera postivos.
Solución
Aquí se presenta un resumen sucinto de la resolución. Para estudiar los pasos más detallados puede descargar el borrador Resolución de viga articulada-empotrada – borrador.
Elástica de la viga
Para resolver el problema, se plantea la ecuación de la elástica en su forma derivada en cuarto orden:
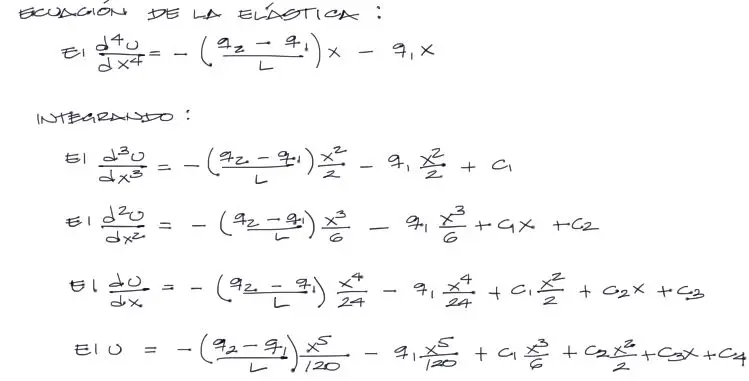
El miembro derecho de la ecuación es simplemente la ecuación de la carga trapezoidal, donde el signo (-) indica la dirección de la carga hacia abajo. Se puede comprobar fácilmente que si x=0 q=-q1, y si x=L q=-q2.
Intergando 4 veces la elástica de la viga obtenermos respectivamente, la ecuación del cortante, del momento flector, de la pendiente y de la deflexión de la viga. Al integrar 4 veces obtenemos también 4 constantes de integración C1, C2, C3, C4 que debemos resolver y determinar.
Condiciones de contorno
Las condiciones de contorno se obtienen a partir de los apoyos físicos de la viga. En ese sentido, en el extremo izquierdo no existe desplazamiento vertical ni momento flector. En el extremo derecho no existe deflexión ni giro. esto expresado matemáticamente resulta en:

Constantes de integración
Las condiciones de contorno de arriba se reemplazan en las ecuaciones donde aparecen las variables impuestas. Por ejemplo la primera ecuación de contorno consiste en X=0 —> u = 0. En ese sentido se reemplaza X=0 y u=0 donde se hace presente “u” en la forma sin integrar, o sea, en la última ecuación de la elástica. De la misma manera se reemplazan todas las condiciones sobre las ecuaciones de la elástica.
Se forma un sistema de 4 ecuaciones con 4 incógnitas (las constantes) que resueltas resuntan en:
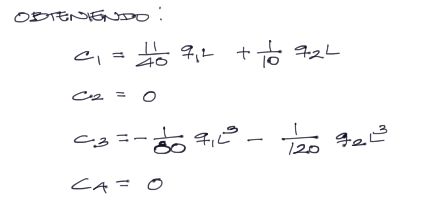
Para el detalle de la resolución de este sistema consultar el borrador cuyo enlace está arriba.
Cortante (Ecuación y valores extremos)
Con las constantes encontradas, puede reemplazarse la constante C1 en la tercera derivada de la elástica. Graficando queda:
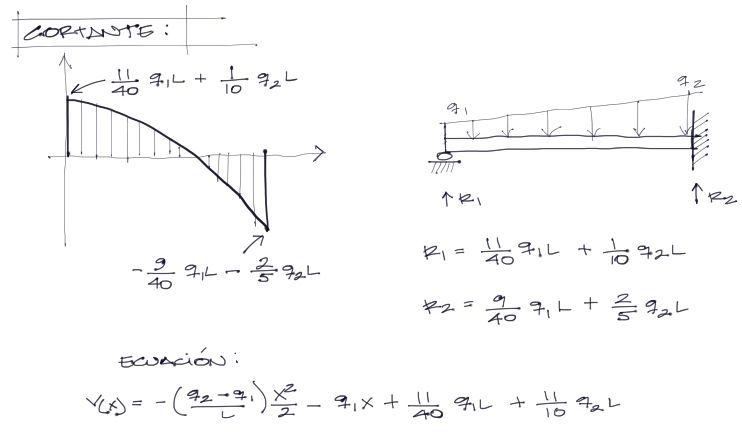
Se entiende que de la gráfica del cortante (cuya ecuación se encuentra en la parte inferior del gráfico) pueden encontrarse las reacciones de fuerza vertical de los extremos de la viga.
Momento flector
De la misma manera que para el cortante, pueden reemplazarse C1 y C2 en la segunda derivada de la elástica y graficar la ecuación.
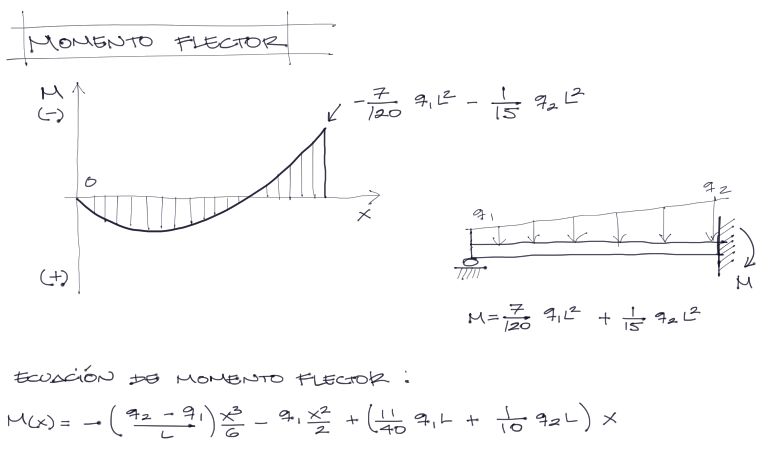
En este caso los momentos condicen con las condiciones de contorno donde en el extremo izquierdo el momento flector es cero. Además del extremo derecho de la gráfica puede extraerse la magnitud de la reacción de momento del empotramiento, que tracciona las fibras superiores y cuya magnitud se muestra en la gráfica.
Deflexión vertical de la viga
Finalmente reemplazando las cuatro constantes en la ecuación sin derivada de la elástica y despejando “u” de la rigidez, se obtiene la ecuación de la deflexión de la viga. Esta es la siguiente:
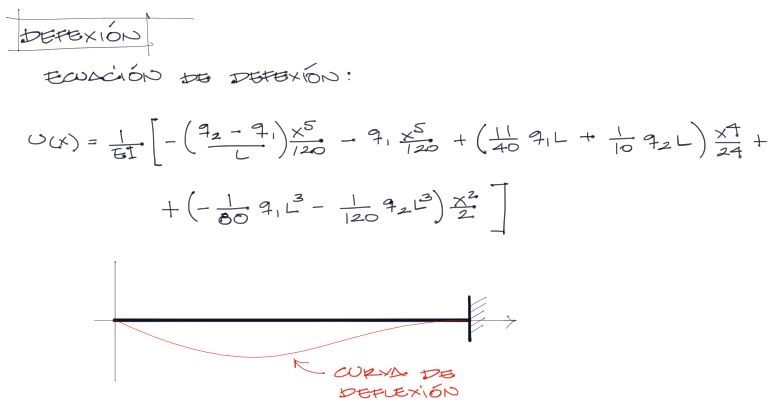
Conclusiones
El propósito práctico de tener la resolución de esta viga en particular junto con la viga “empotrada-articulada” y la “articulada-articulada” es que, a partir de estas soluciones pueden encontarse las cargas equivalentes para la resolución de pórticos con articulaciones por el método de rigidez. Esto se verá en la zona de “Elementos Finitos” de este blog.
autor: Marcelo Pardo