Planteamiento del problema
Por el método de la elástica encontrar las solicitaciones en los extremos de la viga y ecuación de la deformada (deflexión). La viga tiene una longitud L y rigidez constante EI.
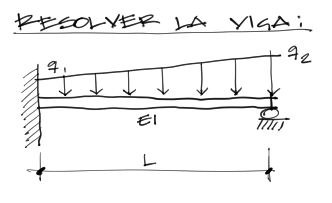
Ecuación de la elástica
La ecuación de la elástica para una rigidez constante y para la carga trapezoidal del enunciado es:
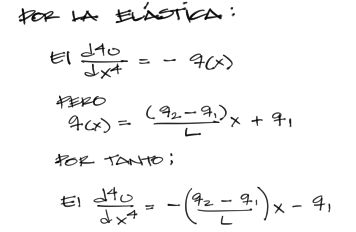
Se deduce la ecuación de la recta que es proyectada por la carga, para dos valores q1 y q2 cualesquiera.
Integración de la elástica
Para conocer el comportamiento completo de la viga, se debe integrar la ecuación de la elástica 4 veces. La primera integral representa el cortante. La segunda representa el momento flector de la viga. La tercera representa la pendiente de deflexión y la cuarta la deflexión. Se tiene entonces lo siguiente.
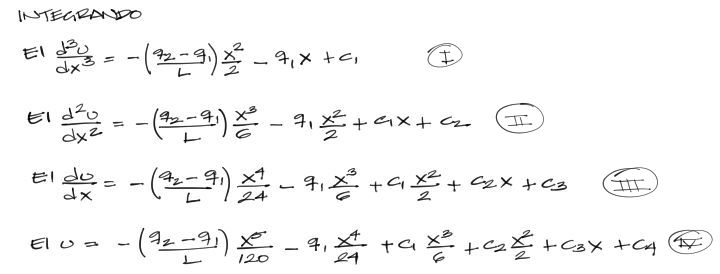
Al integrar las ecuaciones, se generan constantes de integración que se deducen junto con las condiciones de contorno.
Condiciones de contorno
Éstas condiciones tienen siempre una representación física. En el caso de la viga representan las condiciones de los apoyos. En el apoyo izquierdo tanto el desplazamiento vertical “u” como la pendiente de deflexión “du/dx” son cero. En el extremo derecho la deflexión es nula por el apoyo movil, y también el momento flector. Se tiene entonces:
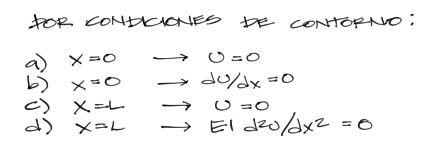
Estas ecuaciones de contorno deben reemplazarse en las ecuaciones arriba integradas. Las dos primeras condiciones se reemplazan en la ecuación de la deflexión y pendiente de deflexión respectivamente (III y IV). La tercera condición se reemplaza en la ecuación de la deflexión (IV) y la cuarta condición se reemplaza en la ecuación de momento flector (II).

A partir de estos reemplazos pueden encontrarse las Constantes de Integración C1, C2, C3, C4.

Con estas constantes encontradas ya se tiene toda la información de la viga para ser interpretada.
Cortante y reacciones
Si reemplazamos las constantes de integración en la ecuación I, se tiene la ecuación de cortante para la viga:
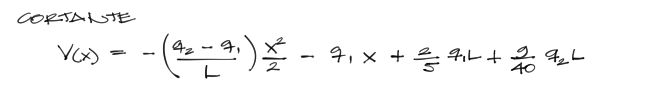
Reemplazando X con 0 y con L se encuentra el cortante en los extremos de la viga.

Los cortantes en los extremos son directamente las reacciones de fuerza vertical de la viga.
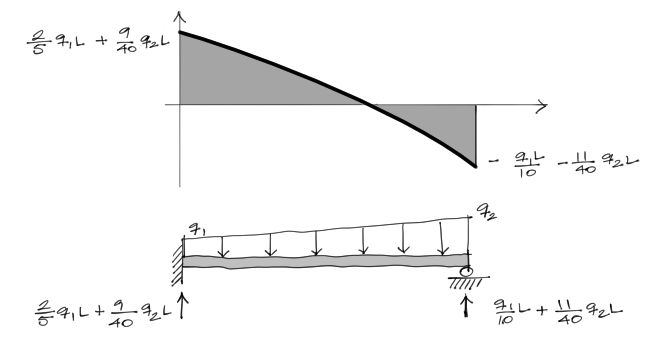
Momento flector
De la misma manera que para el cortante, se pueden encontrar las solicitaciones de momento para todos los puntos de la viga a partir del reemplazo de las constantes de integración dentro de la ecuación (II). Se tiene con esto
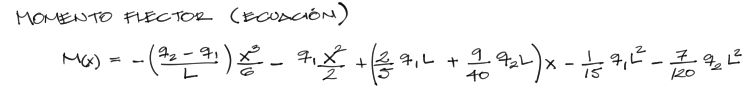
Los momentos en los extremos, encontrados a partir de X=0 y X=L son:
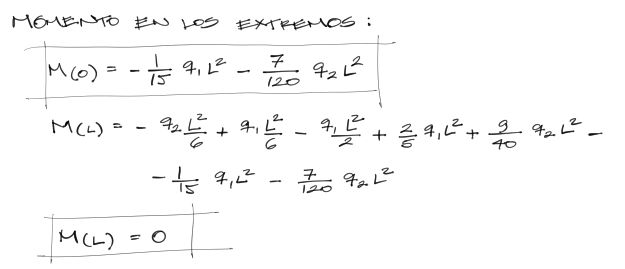
La gráfica de momento flector con los momentos extremos se interpretan entonces de la siguiente manera:
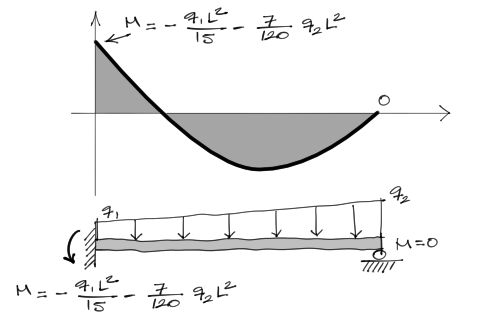
Ecuación de la deflexión
Reemplazando las constantes de integración en la última ecuación de la elástica (IV) se obtiene:
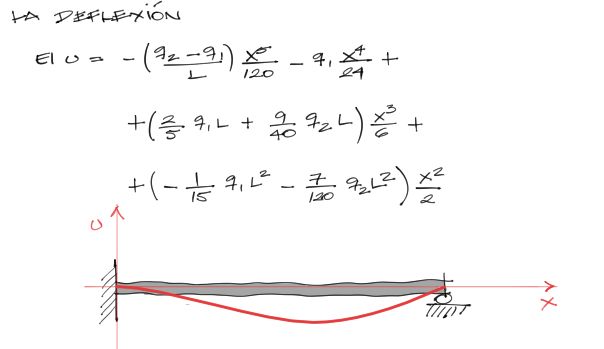
Aplicaciones prácticas
Todas estas fórmulas sirven para conocer las cargas equivalentes en los extremos de una viga articulada en el extremo derecho, en el método de rigidez.
En el diseño de concreto reforzado sirve para conocer las solicitaciones de una viga apoyada en muros de mampostería o muros de concreto que no sean capaces de desarrollar una union empotrada entre viga y muro debido a su espesor reducido.
autor: Marcelo Pardo