Enunciado
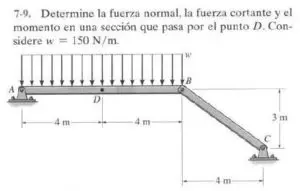
Se pide encontrar los diagramas de momento flector y cortante para la viga mostrada en la imagen:
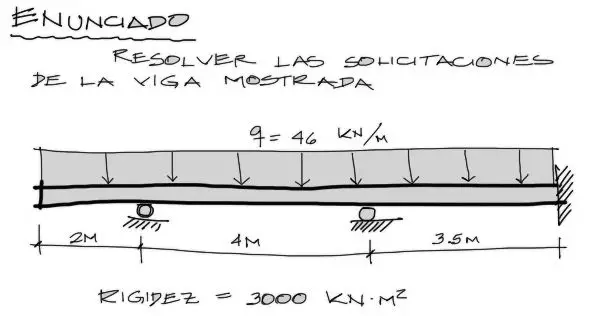
El problema es distinto a problemas clásicos, pues el estudiante no entiende muy bien como procede el cálculo cuando existe un voladizo en un extremo.
Solución
Breve teoría
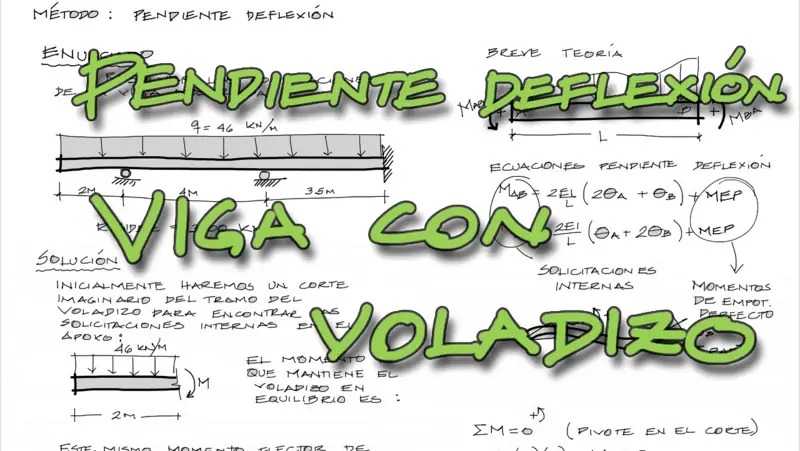
Para uniformar nomenclatura, se hace un breve recuerdo a las ecuaciones de pendiente deflexión mediante la siguiente imagen
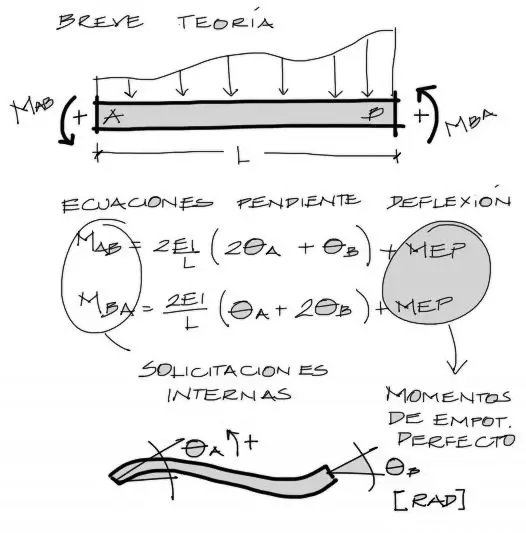
Para un tramo de viga entre dos apoyos, las variables que aparecen son las mostradas:
- Mab y Mba son las solicitaciones internas de momento flector en el tramo. se miden en sentido antihorario positivo
- Los giros θA y θB se miden en radianes, en sentido antihorario positivo
- Los MEP (momentos de empotramiento perfecto) son los momentos reacción en una viga equivalente a la del tramo analizado pero empotrada en los extremos y con la misma carga del tramo. Estos MEP también toman valores positivo antihorario y negativo horario.
- EI es la rigidez del tramo
- L es la longitud entre apoyos del tramo analizado
Para un detalle mas pormenorizado de la teoría puedes ir al link: Teoría de pendiente deflexión. Si además quieres conocer de donde salen las fórmulas del método pendiente deflexión, puedes ir al link Demostración de fórmulas del método pendiente deflexión.
Qué se hace con el voladizo?
El primer paso es encontrar la solicitación que produce el voladizo sobre el resto de la viga. Para esto aislamos el voladizo desde el extremo izquierdo hasta el apoyo derecho.
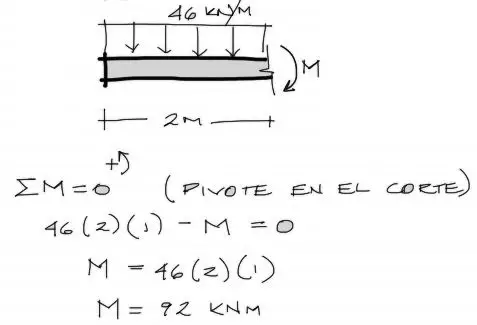
Luego de aislar el voladizo, aparecen solicitaciones internas en el corte derecho imaginario. Este momento flector solicitación interna lo asusmimos traccionando las fibras superiores pues seguramente este es el sentido correcto en el que el momento trabajará para equilibrar el voladizo. Haciendo pivote en el extremo derecho del voladizo, equilibramos a momento todo este voladizo. Nota que no dibujo el cortante pues para este punto no es necesario. El método de pendiente deflexión trabaja solo con momentos y no con cortantes.
Viga equivalente
Una vez encontrado el momento flector de 92 KNm, el mismo momento en magnitud pero opuesto en dirección aparece al otro lado del corte imaginario. Dibujando la viga con la solicitación interna producto del voladizo se tiene entonces:
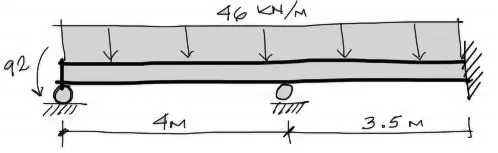
La viga mostrada es una viga equivalente que no lleva ya el voladizo pero lleva un momento interno (solicitación) equivalente que carga a la viga con un momento equivalente a la carga del voladizo.
Ecuaciones de pendiente deflexión
Para escribir las ecuaciones de pendiente deflexión debemos ahora poner nombres a los apoyos. Los llamaremos A B y C

Luego separamos los tramos y dibujamos las solicitaciones internas Mab, Mba, Mbc y Mcb. Estos momentos internos pueden leerse Mab = “momento en A mirando hacia B”, etc
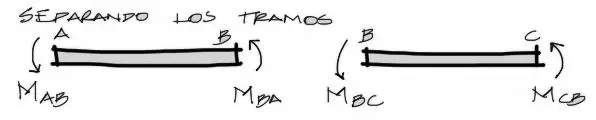
Posteriormente escribimos las ecuaciones de pendiente deflexión. Dos ecuaciones por cada tramo, y con las variables AyB para el primer par y ByC para el segundo par de ecuaciones. Genericamente las ecuaciones son las siguientes:
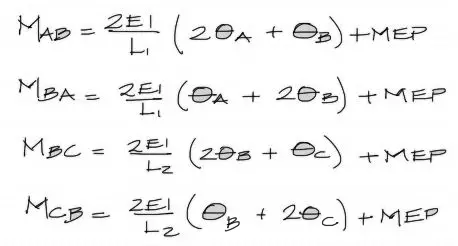
Reemplazo de datos
Los primeros datos a reemplazar serán los de los momentos de empotramiento perfecto. Estos MEP se obtienen de tablas y consisten en momentos de reacción en los empotramientos de una viga equivalente a la viga del tramo analizado, pero que en los extremos está empotrada. Para nuestro caso, en cargas distribuidas constantes los MEP en cada extremo valen qL²/12, con los signos mostrados en la imagen.
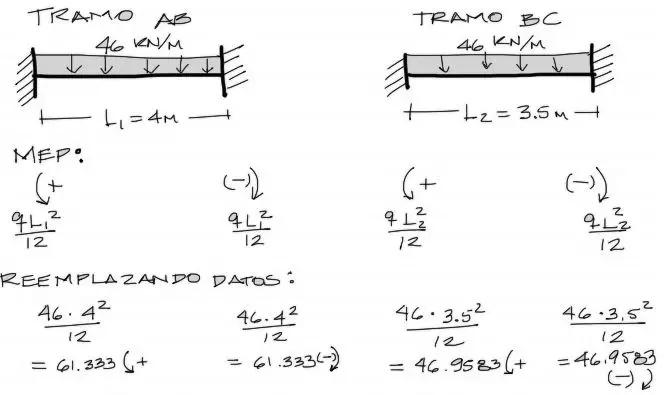
Estos valores con los signos de los giros se reemplazan en las ecuaciones de pendiente deflexión. Por otro lado se reemplazan las longitudes L1 = 4m y L2 = 3.5m Finalmente la rigidez que es de EI = 3000 KNm²
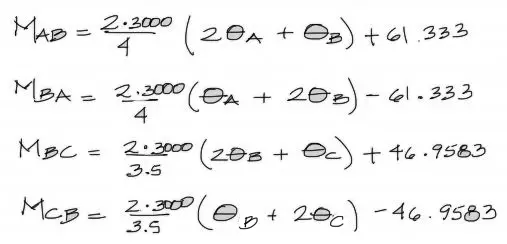
Además de los reemplazos ya hechos, sabemos que la solicitación interna Mab es igual a 92, positiva según la dirección de la flecha del gráfico de la viga equivalente. Por otro lado en el apoyo B, se deben sumar los momentos flectores Mba+Mbc e igualarlos a cero para lograr el equilibrio en el corte.
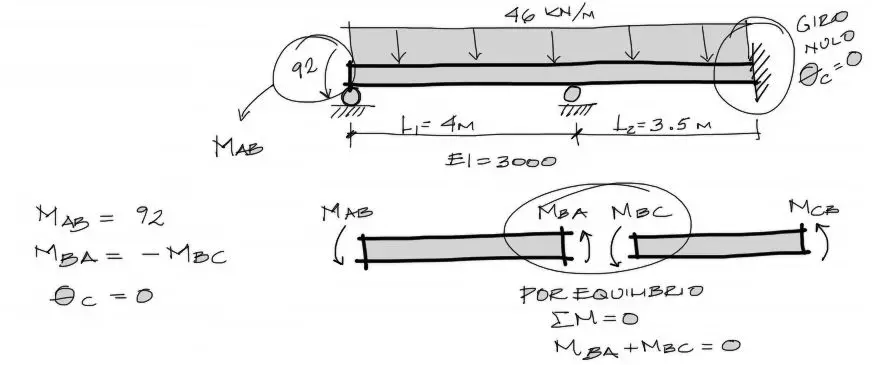
Finalmente, la última condición de contorno indica que debido al empotramiento el giro en este punto C es cero.
El sistema de 7 ecuaciones con 7 incógnitas queda entonces de la siguiente manera:
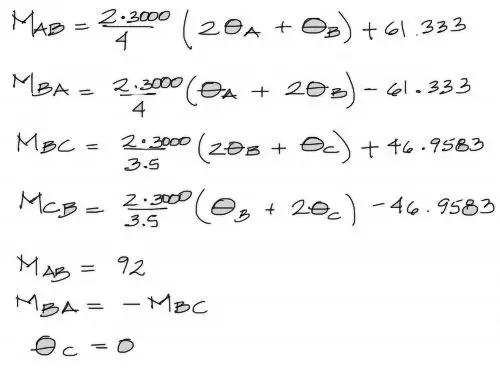
Resolución del sistema de ecuaciones:
El anterior sistema de 7 ecuaciones con 7 incógnitas se puede escribir llevando todas las variables al lado izquierdo de las ecuaciones y los términos independientes al lado derecho de las ecuaciones, de la siguiente forma:

Luego, los coeficientes de las variables, ordenados se van anotando en una matriz 7×7, acompañados de un vector 7×1 de las variables y todo igualado a los términos independientes:

Este sistema se resuelte por el método que más prefieran, siendo uno de los más recomendables el de Gauss Jordan.

Dibujo de solicitaciones
Las solicitaciones dibujadas en la viga a partir de los resultados en la imagen de arriba se logran de la siguiente manera. Se dibujan Mab, Mba, etc en cada extremo de cada tramo cuidando los sentidos de cada solicitación de momento. Nota que siempre los momentos en los cortes de tramos internos deben igualarse en magnitud y oponerse en sentidos de giro
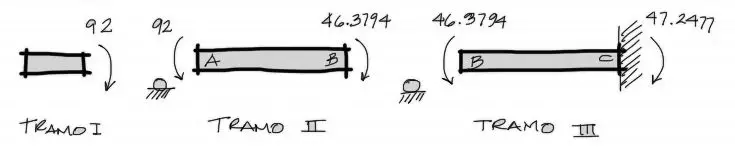
Equilibrio interno de solicitaciones de cortante
Las solicitaciones de momento flector están resueltas, sin embargo aun no conocemos los cortantes de la viga. Para lograr esto, seguimos trabajando con los tramos aislados enumerados del I al III, de la siguiente manera
Para el tramo I, solo existe una incógnita de cortante. La dirección hacia abajo de este cortante va acorde a la convención de signos para diagramas de cortante, donde a la derecha del corte apunta hacia abajo y a la izquierda del corte va hacia arriba. Ya que tenemos una sola incógnita, aplicamos solo la suma de fuerzas verticales igualada a cero para conocer V:
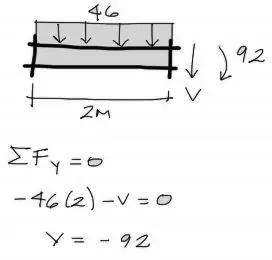
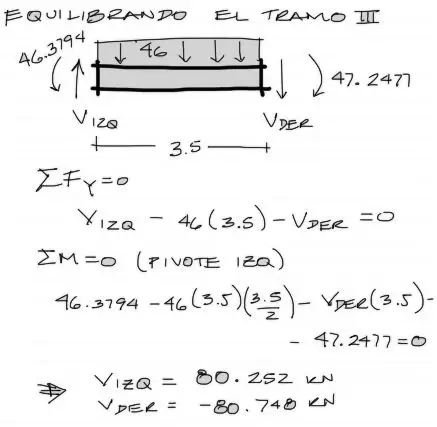
Para el tramo II, realizamos el equilibrio en base a un sistema de 2 ecuaciones con 2 incógnitas pues no conocemos los cortantes Vizquierdo ni Vderecho:

El mismo procedimiento se realiza para el tramo III
Gráfica de cortantes
Los cortantes encontrados arriba en base a la convención de signos mencionada se grafican acompañando los signos de las soluciones en el diagrama mostrado a continuación. Se sabe que el diagrama de cortante en este caso está unido por líneas rectas con pendiente ya que las cargas son distribuidas constantes. Esto siempre suceda ya que la integral de la carga es el cortante, y para rectas con pendiente cero (cargas) la integral será una recta con pendiente (cortante)
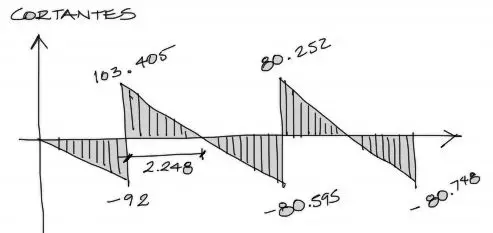
La cota del segundo tramo, de 2.248 se obtiene a partir de la relación de triángulos siguiente:
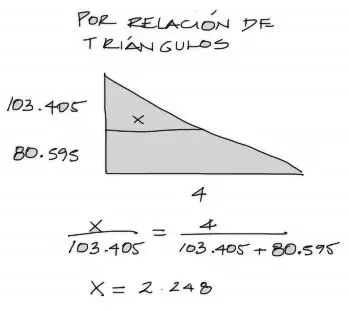
Este dato del punto donde el cortante se hace cero es necesario para encontrar más adelante el punto donde el momento se hace máximo
Gráfica de momentos flectores
A partir de los resultados del método de pendiente deflexión se pueden dibujar los momentos flectores en los apoyos. Sin embargo los momentos máximos al centro de los tramos II y III deben obtenerse a partir del punto donde el cortante se hace cero.
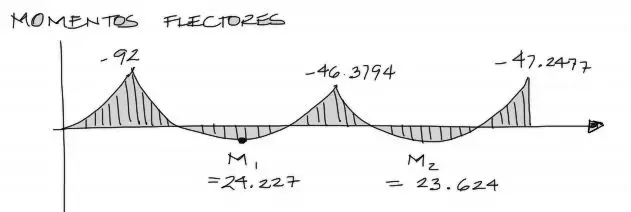
Los momentos -92, -46.37 y -47.24 tienen signo negativo pues los momentos por pendiente deflexión traccionan las fibras superiores de la viga en este punto (Y la convención de signos para diagramas de momentos flectores indica que el momento es negativo si tracciona fibras superiores y positivo si tracciona fibras inferiores). Por otro lado, para obtener los momentos máximos positivos se debe realizar el siguiente cálculo:
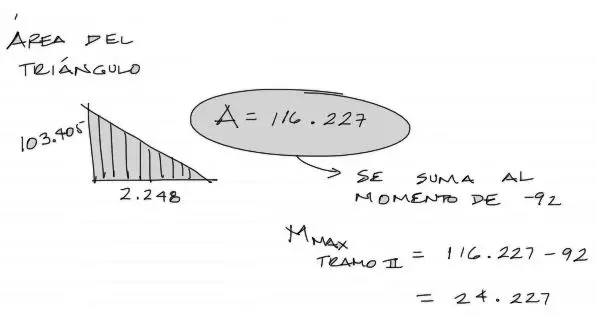
El momento flector resulta de la integración (área debajo de la curva) del cortante. Por tanto si partimos del momento de -92, para llegar al momento M1, debemos sumar a -92 el área del triángulo del cortante desde 103.405 hasta el punto donde se hace cero a una distancia de 2.248m desde el apoyo móvil izquierdo. La operación en la gráfica arriba hace precisamente eso. Al final el momento M1 = -92 + 116.227 = 24.227 KNm. Se realiza el mismo procedimiento para el momento máximo M2 del tercer tramo. Y con esto termina el ejercicio. Te invito a verificar este momento M2 encontrado.
VIDEO
El vídeo de este ejercicio explicado en 11 minutos lo encuentras en VIDEO DE VIGA CON VOLADIZO POR PENDIENTE DEFLEXIÓN
autor: Marcelo Pardo