Enunciado
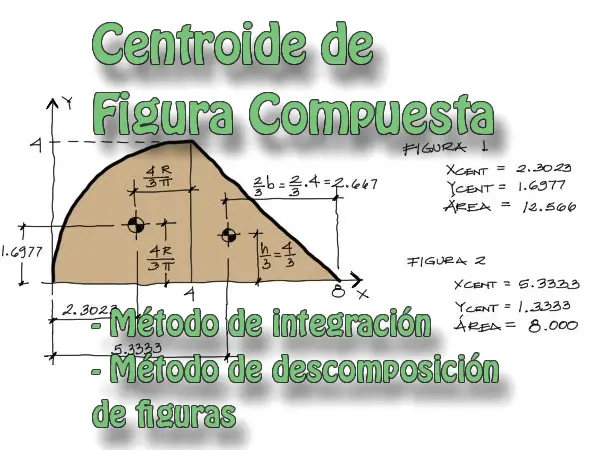
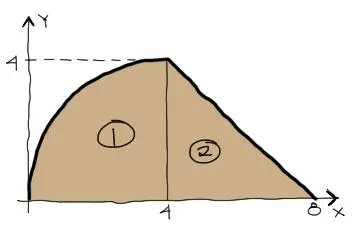
Resolver el centroide de la siguiente figura compuesta:
Se pide resolver el centroide de las dos figuras por separado y luego el centroide de la figura compuesta completa.
Resolución
Centroide em X mediante integración
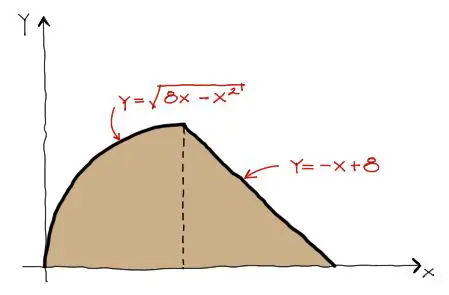
Dibujamos la pieza circular suelta. Luego debemos conocer los límites que enmarcan esta curva. Para eso reemplazamos Y=0 en la ecuación pues esos serán los dos puntos donde la curva intersecta con las X. Resolviendo esta ecuación se obtienen dos resultados de X: X=0 y X=8. A partir de estos puntos, deducimos que el radio del círculo es R=4. Para la interesección del triángulo con las X, reemplazamos Y=0 y despejamos X y encontramos que la recta intersecta con las X en X=8:
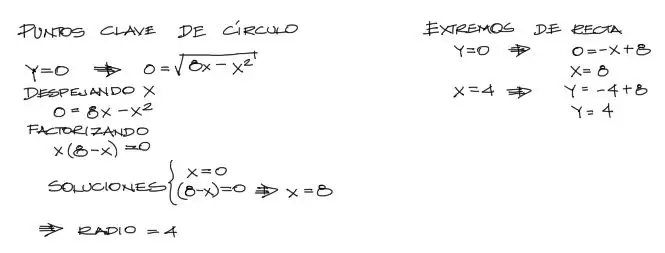
Finalmente graficando la pieza:
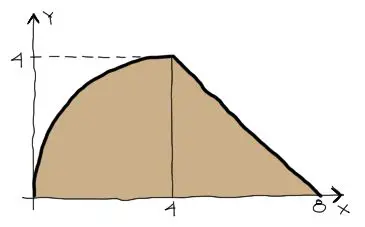
Conocidos los límites de la pieza, ahora podemos aplicar las fórmulas de centroide tanto en X como en Y. Comenzamos con la fórmula genérica del centroide en X.
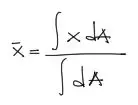
Como tenemos dos curvas sobre las cuales trabajar, se deberá separar la integral del numerador y del denominador en dos tramos, de la siguiente manera:
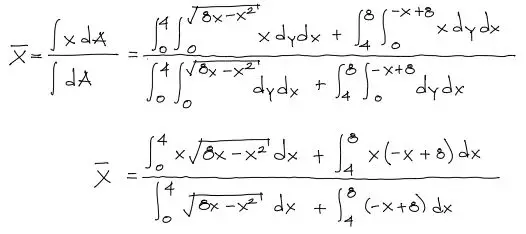
Se pueden aprovechar ciertas herramientas tecnológicas para resolver estas integrales de manera rápida y fácil. Puedes visitar el enlace para ver en detalle como resolver cada una de las 4 integrales en Octave (o en Matlab, que viene siendo lo mismo). Resolución de integrales con Octave
Se obtiene de la resolución numérica de dichas integrales, lo siguiente:
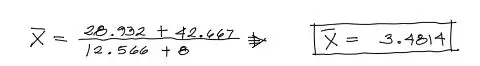
Centroide en Y mediante integración
De la misma manera como se resolvió el centroide en X, procedemos con el centroide en Y

Sobre las integrales y los diferenciales de Area
Probablemente no estés acostumbrado a este tipo de integración descomponiendo dA = dy*dx, sin embargo esta manera de integrar integrales de dos variables es la más ordenada y sistemática.
Además notarás que siempre la integral interna está en función de Y. No importa si el centroide que calculemos sea respecto a X o respecto a Y, la integral respecto a Y siempre se evalúa primero. Esto se debe a que los límites superior e inferior tienen a Y como la variable dependiente.
Resolución mediante tablas de centroides de figuras simples
En vez de evaluar el centroide de las dos figuras compuestas en base a las ecuaciones que las delimitan y en base a integrales, se puede utilizar el siguiente par de fórmulas:

En este caso contamos con dos figuras simples que componen la figura compuesta.
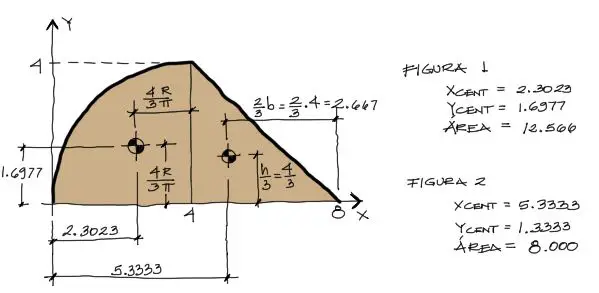
A partir de tablas de centroides e inercias de figuras se puede encontrar tanto el centroide como la superfice de ambas superficies. El enlace proporcionado tiene los datos requeridos. Entonces para nuestro ejercicio:
Finalmente aplicando las fórmulas citadas arriba, se tiene:
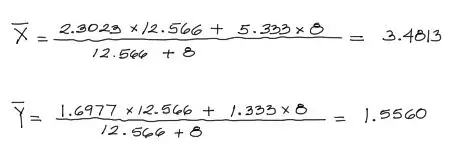
Con esto concluye el ejercicio por los dos métodos conocidos
autor: Marcelo Pardo