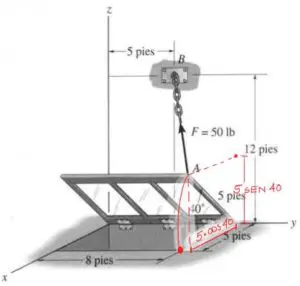
Un recordatorio de Centroides por el Método Clásico
En el método clásico cuando se tiene una sección como la mostrada en la figura, se debe realizar una discretización de la figura a piezas más simples.
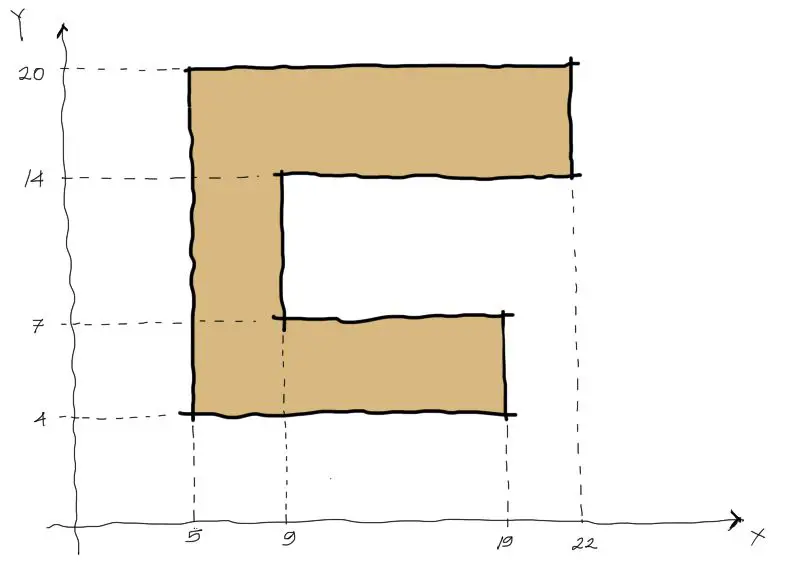
Se debe escoger un tipo de división que genere figuras básicas de rectángulos , triángulos o semicírculos. En este caso se puede descomponer a la sección en puro rectángulos.
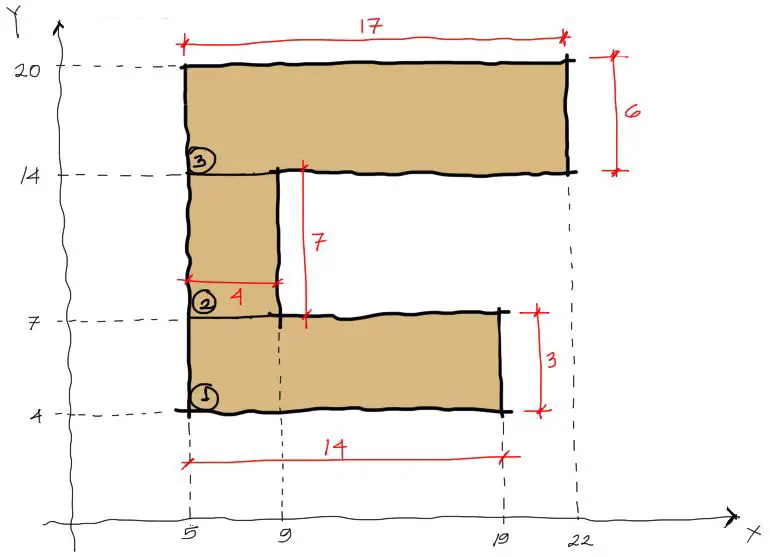
El siguiente paso consiste en encontrar los centroides de cada figura simple y también su superficie. Todos estos datos pueden acumularse en una planilla de cálculo.
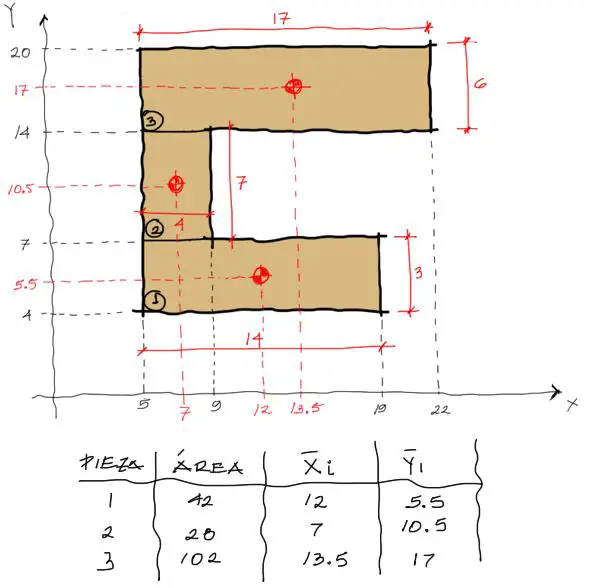
El paso final es aplicar las fórmulas de cálculo de inercia. Este último paso suele ser mecánico y sin mayor dificultad. Donde puede surgir la mayor fuente de error manual es en el paso de encontrar los centroides de cada figura como en la imagen arriba.
Entonces aplicando las fórmulas de centroide se tiene:

Y el centroide de la figura queda como en la imagen siguiente.
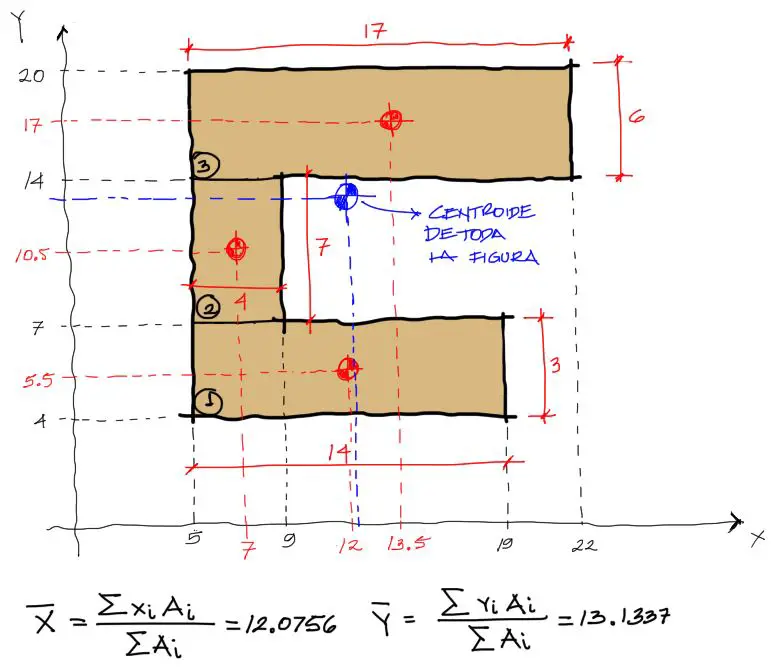
De esta manera se han obtenido los centroides de figuras compuestas por el método enseñado en todos los libros de estática y mecánica de materiales.
El método de centroides por Coordenadas
El método de centroide por coordenadas es mucho más mecánico. El problema radica en el entendimiento y programación de las fórmulas. Las fórmulas que te enseñaré a continuación corresponden al centroide de un polígono cerrado.
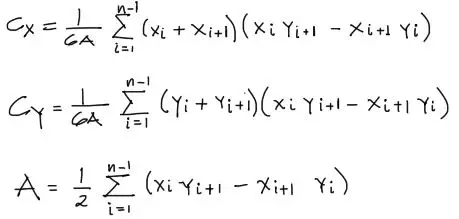
Se entenderán mejor las fórmulas mostradas con un ejemplo.
Ejemplo con un triángulo
Si por ejemplo tenemos un triángulo como el de la figura, se deben acomodar las coordenadas en una tabla, donde el primer nudo se debe repetir al final de la tabla para cerrar el polígono. La numeración de vértices o nudos debe ser en sentido antihorario para que las áreas calculadas salgan positivas. Si se hiciera la numeración en sentido horario, el área calculada saldrá negativa.
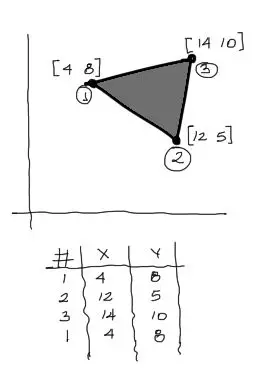
Luego, las coordenadas x de todos los puntos se enumeran x(1), x(2), x(3) y x(4) en nuestro caso. Lo mismo se hace para las coordenadas Y.
Al aplicar las fórmulas citadas en el anterior subtítulo, se tiene entonces:
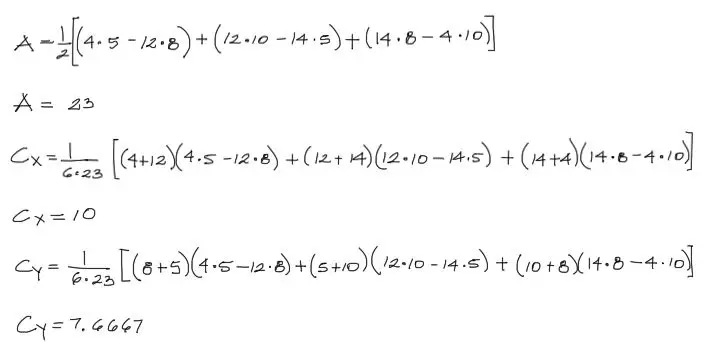
Y luego de operar se tienen los resultados correspondientes.
Ejemplo más complejo
Ahora apliquemos el ejemplo del inicio, con la figura poligonal en C. La numeración antihoraria y coordenadas quedan así:
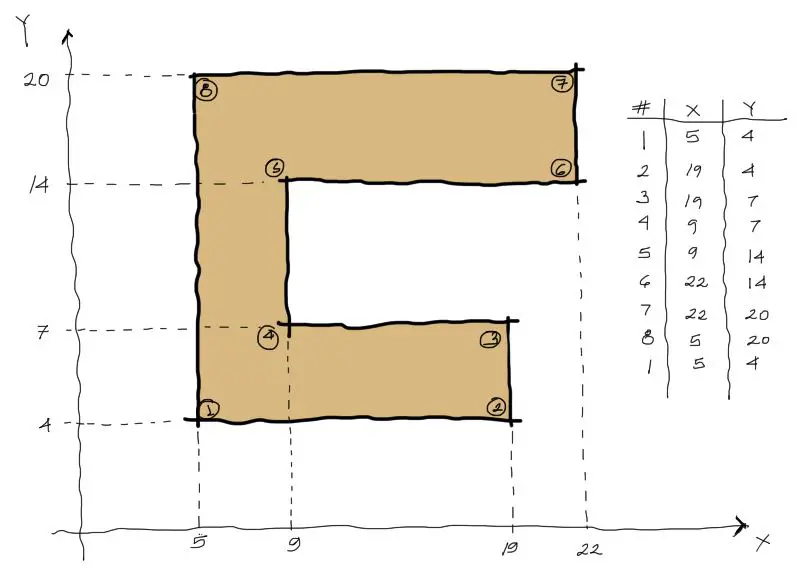
En este caso ya es más pesado hacer un detalle de las operación y reemplazos en las fórmulas mostradas. Es por eso que se debe aplicar un programa de cálculo con estructuras en bucle o repetitivas para alivianar el cálculo repetitivo.
Programa en Octave
El tutorial de programación del algoritmo anterior en Octave lo tengo en el siguiente vídeo (que está disponible en la zona de miembros del canal).
El resultado
Aplicadas las fórmulas se obtiene el mismo centroide obtenido por el anterior método, pero a un coste manual mucho menor pues lo único en lo que debemos concentrarnos es en ingresar las coordenadas del perímetro del polígono.
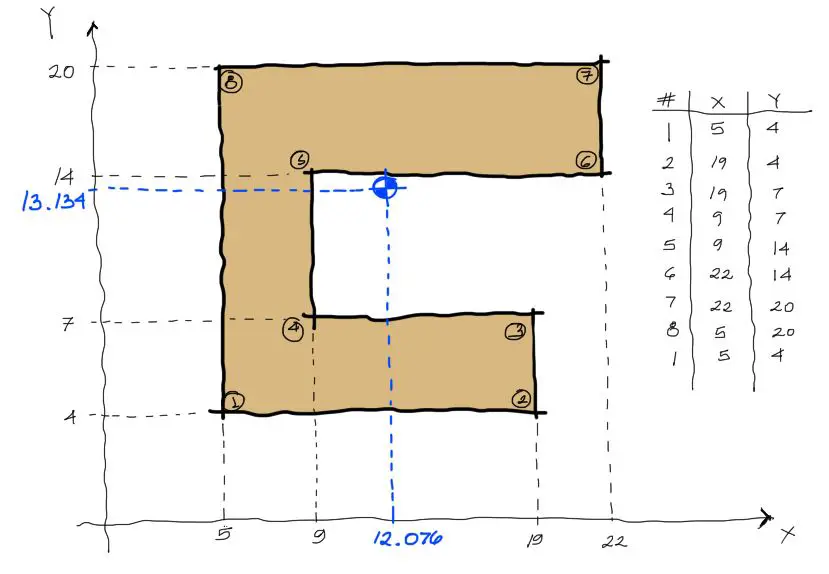
En el programa se obtiene exáctamente lo mismo:
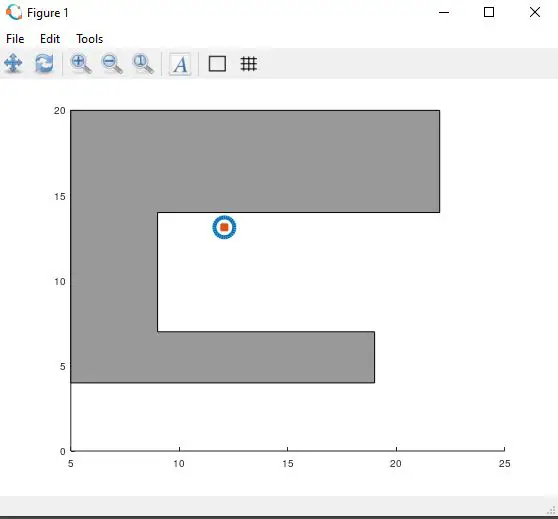
autor: Marcelo Pardo
←←← VOLVER A TABLA DE CONTENIDO DE RESISTENCIA DE MATERIALES ←←←