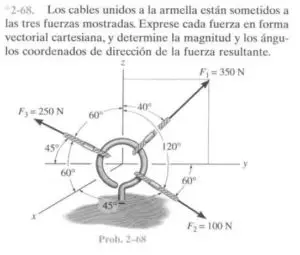
Enunciado
Se pide resolver tanto las reacciones como las solicitaciones internas de la cercha mostrada a continuación:
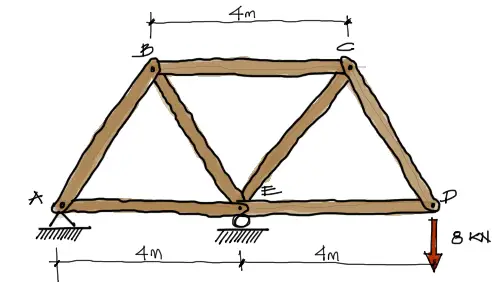
Todas barras miden 4m, por tanto los triángulos formados son equiláteros y todos los ángulos internos son de 60°.
Por tratarse de una cercha isostática, no son necesarias las secciones de la cercha. Despreciar el peso propio de la estructura.
Estabilidad externa
El primer paso para la resolución clásica de cualquier cercha isostática consiste en el equilibrio externo de cuerpo rígido. Entonces, verificando que existan tres incógnitas para las tres ecuaciones que se plantean en 2 dimensiones:
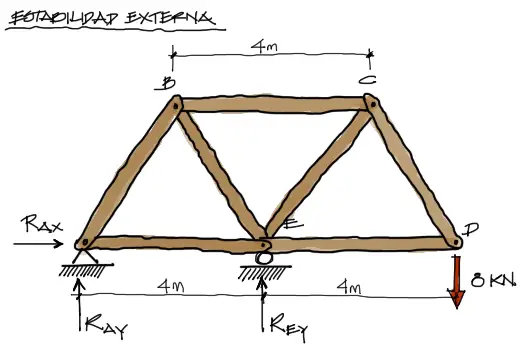
Gracias a la configuración de los apoyos, se generan las tres componentes de reacciones mostradas arriba. Se aplican entonces primero las dos ecuaciones de suma de fuerzas.
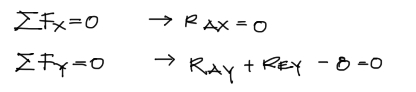
Ninguna de las dos incógnitas verticales puede aún resolverse. Entonces aplicamos la tercera ecuación de equilibrio de cuerpo rígido: Suma de momentos respecto a un punto. Escogemos en este caso el punto A como pivote y realizamos el cómputo de fuerzas y brazos tomando como positivo el giro antihorario.
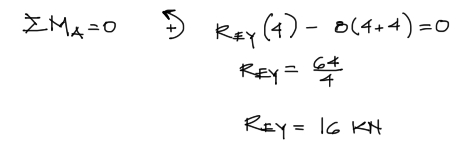
Si quieres entender a profundidad el concepto de momento de fuerza desde un punto de vista escalar (que es el que se aplicó en esta ecuación) puedes ver mi publicacion Concepto escalar y vectorial de momento de fuerza.
Encontrada la reacción en el punto E en dirección Y, se puede reemplazar este resultado en la ecuación de suma de fuerzas verticales dos imágenes arriba, obteniendose:
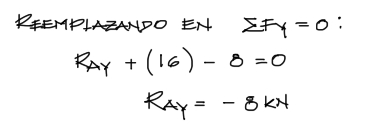
Luego, con todas las reacciones encontradas, se procede al cálculo de las solicitaciones internas.
Solicitaciones internas
Gracias a la simetría tanto en la geometría de la estructura como en las cargas y reacciones, basta con resolver un par de nudos para conocer las solicitaciones de toda la estructura. Las solicitaciones que encontremos en un nudo a la izquierda serán identicas a la del nudo equivalente en el extremo derecho. Esto solo es posible gracias a que las reacciones también son simétricas con la carga. Si bien existe una reacción horizontal en el extremo izquierdo que no existe al lado derecho, la simetría se mantiene ya que la reacción horizontal es cero.
Nudo A
Debemos buscar un nudo al que concurran solamente dos barras cuyas solicitaciones no se conozcan, debido a que se tienen dos ecuaciones para resolverlas.
Por tanto si comenzamos con el equilibrio interno del Nudo A:
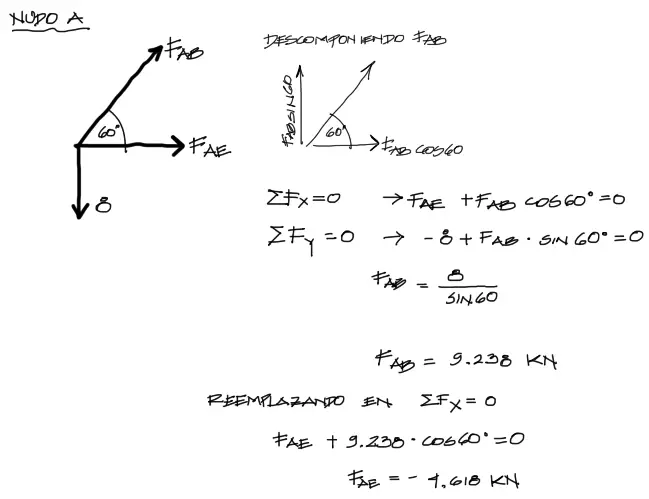
A la derecha del equilibrio del nudo se muestra la descomposición de las fuerzas inclinadas. Luego abajo la suma de fuerzas en X y luego la suma de fuerzas en Y.
Se asume que las solicitaciones están en tracción de inicio (vectores saliendo del nudo). Resueltas las ecuaciones, el signo indica si la barra está a tracción (positivo) o compresión (negativo).
Nota que para el equilibrio de nudos no necesitamos aplicar ecuación de suma de momentos de fuerza, ya que todas las fuerzas concurren en un mismo nudo.
Nudo B
Habiendo encontrado la solicitación de la barra A-B, podemos equilibrar el nudo B pues de las tres barras que concurren en este nudo, solo dos ya son incógnitas.
Si la barra está en tracción (positiva) entonces debe salir del nudo B (igual que del nudo A, para estar en equilibrio).
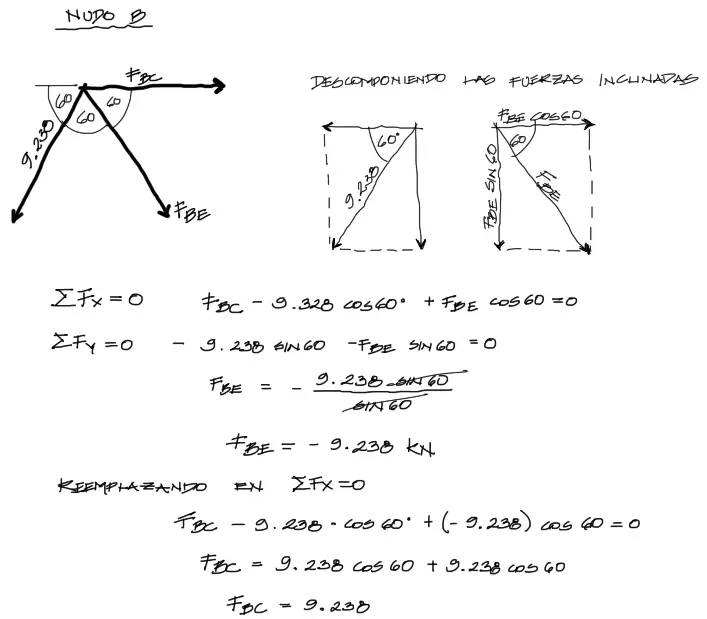
Los demás nudos
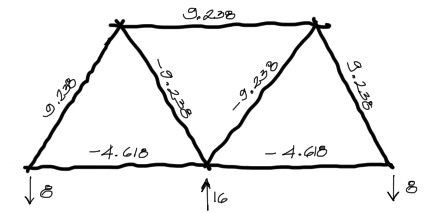
Habiendo resuelto ambos nudos, se tienen 4 barras de la izquierda resueltas quedando solo 3 barras del extremo derecho por resolver. Como mencionamos, la cercha es simétrica, por tanto las solicitaciones de la izquierda serán iguales a las de la derecha y se tiene:
Vídeo
La resolución de este mismo ejercicio en vídeo la tienes a continuación:
autor: Marcelo Pardo