Introducción
El estudio de columnas esbeltas puede hacerse extenso, sin embargo procuraré en este artículo resumirlo lo más posible para el caso más general.
Te recomiendo que si ya entiendes el tema de columnas esbeltas, sigas esta teoría junto con el ejemplo que puedes encontrar en el PRESENTE LINK.
En general una columna comienza a considerarse esbelta cuando los momentos de segundo orden comienzan a tomar importancia frente a los momentos de primer orden producto del cálculo estático.
Momentos de segundo orden
Los momentos flectores de segundo orden son momentos que se generan producto de la multiplicación de la carga axial multiplicada por la excentricidad de las deformaciones de los momentos flectores de primer orden. Estas deformaciones de primer orden en general están causadas por sismo, viento o cualquier carga lateral.
Si llamamos a esta excentricidad como «Delta» y a la carga axial «P», los momentos de segundo orden se obtienen de la multiplicación de las cargas P por el desplazamiento Delta. De ahi el nombre que recibe este tipo de momentos: Análisis P-Delta o P-Δ
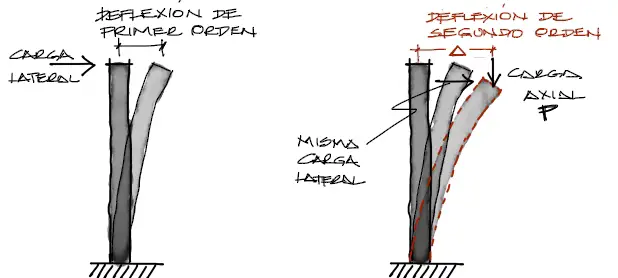
Sin embargo, el problema es más complejo de lo que parece, pues el proceso es iterativo ya que el momento generado por el efecto P-Δ, a su vez genera otro desplazamiento de la columna con nuevas excentricidades y un nuevo momento de segundo orden, incrementado al anterior, hasta que toda la estructura converja en el equilibrio o colapse.
Menos mal existen programas que pueden hacer este tedioso trabajo por nosotros.
Forma de cálculo de los momentos extremos según la norma ACI 318-14
Momentos de Primer + Segundo orden en ELU
Cuando afrontamos el problema de columnas, la norma ACI indica que los momentos extremos de primer y segundo orden (estáticos y P-Delta) deben incrementarse para salvar excentricidades accidentales no tomadas en cuenta, y cambio de rigideces de la sección de la columna por fisuración.
Asumiremos en este texto que los momentos P-Δ ya han sido calculados (por el programa de tu preferencia) y que el momento M en los extremos de la columna se compone por la suma de los momentos producto de cargas verticales más los momentos producto de cargas laterales.
donde:
- M = Momentos de primer y segundo orden Mayorados en Estado Límite Último ELU (momento Flector con P-Δ)
- Mns = Momentos producto de cargas verticales «Non sway»
- Ms = Momentos producto de cargas laterales «sway»
- δs = Factor de mayoración de momentos laterales. Cuando se realizó un análisis P-Delta, δs = 1
Si el pórtico fue calculado con el efecto P-Δ, ya no es necesario el cálculo de esta fórmula, y M se obtiene directamente del modelo estructural. Esta fórmula en realidad sirve para obtener los momentos de segundo orden en función a los momentos de primer orden cuando no se cuenta con un programa que nos calcule estos momentos.
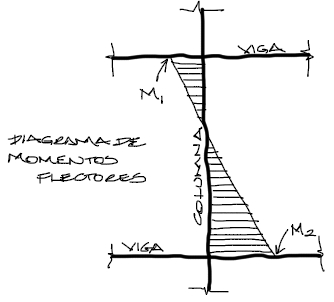
Este momento M con el efecto P-Δ representa el momento más grande en valor absoluto entre los dos extremos de la columna, M1 y M2. M1 será el menor de estos dos momentos y M2 el mayor. Este dato es importante para más adelante.
Factorización de momento de diseño
Podría pensarse que el momento arriba es el momento final con el que se debe diseñar la columna. Sin embargo el momento M obtenido arriba debe incrementarse por un factor δ (delta Non sway) que cubre excentricidades accidentales de la columna, comportamiento plástico y fisuración propios del concreto reforzado. De hecho desde este punto en adelante, la secuencia de pasos siguiente explica cómo encontramos este valor de δ.
Donde:
- δ = factor de mayoración para el diseño
- Mc = Momento de diseño de la columna
- M2 = Máximo momento de segundo orden a partir del análisis elástico de pórtico
A la vez, δ se debe calcular con la siguiente fórmula:
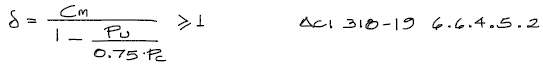
Donde:
- Pc = Carga Crítica axial a Pandeo de la columna en la dirección analizada (se verá como obtenerla más abajo)
- Pu = Carga axial Mayorada en Estado Límite Último (ELU)
Este factor deberá ser siempre mayor o igual a 1. Por otro lado, si se obtuviera un valor de δns menor a 0, se sobre entiende que Pu>0.75Pc y por tanto la sección de la columna escogida no es apta para el diseño. Se debe en ese caso incrementar la sección de la columna.
El valor de Cm de la fórmula anterior se calcula en base a:
Y de esta fórmula de Cm, los momentos M1 y M2 serán:
- M1 = momento más pequeño en un extremo de la columna
- M2 = momento más grande en el otro extremo de la columna
La división de estos dos momentos M1/M2 será positiva cuando formen una curvatura doble en la columna, y positiva cuando se produzca una curvatura simple:
En caso de que existan cargas laterales aplicadas a media altura entre los extremos de la columna, Cm =1. Sin embargo en muy raras ocasiones suele presentarse esta situación. Por otro lado esta fórmula debe aplicarse sólo si el pórtico es Arriostrado a desplazamiento lateral. Si el pórtico es No Arriostrado, Cm = 1.
Por otro lado, el momento M2 de la columna no deberá ser menor a:
- Pu = carga Mayorada en [N]
- h = Altura de la sección transversal (perpendicular a b) medida en [mm]
- M2min = Momento 2 mínimo en [N·mm]
En el cálculo del momento mínimo M2 considero impráctico el manejo de unidades de [N] y [mm]. Por tratarse de una fórmula empírica, no pueden utilizarse otras unidades a menos que cambie la fórmula. En mi caso prefiero utilizar la fórmula en [KN] y [m] siguiente:
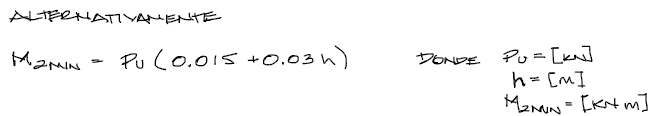
Cálculo de la carga crítica Pc
Líneas arriba se mencionó que Mc debe mayorarse por un factor δns cuya fórmula estaba en función de Pc, que es la carga crítica y que hasta ese momento no se sabía como obtenerla. Ahora se verán las fórmulas de cálculo de esta carga crítica.
Al igual que para resistencia de materiales, Pc responde a:
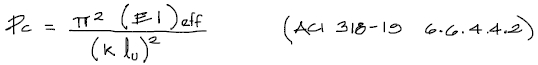
Sin embargo para esta fórmula anterior, la rigidez EI corresponde a la sección fisurada de la columna. Esta rigidez se calculará en breve.
- (EI)eff = rigidez de la sección fisurada de la columna [KN·m²]
- k = Factor de longitud efectiva de la columna [adimensional]
- lu = longitud libre de la columna medida de extremo a extremo [m]
El cálculo de la fórmula mencionada no es trivial ya que depende de factores que pueden variar mucho en función al modelo matemático considerado en el análisis, como se verá más adelante.
Factor de longitud efectiva k
El factor de longitud efectiva en resistencia de materiales es adimensional y está en función del tipo de apoyos en los extremos del elemento, en este caso en los extremos de la columna.
Sin embargo antes de apresurarnos en fijarnos en el tipo de apoyo, debemos saber si la estructura es arriostrada o no arriostrada. En caso de estructuras arriostradas k será en general menor o igual a uno. Sin embargo si la estructura es no arriostrada k será por lo menos uno o mayor.
Es entonces ahora donde nos adentramos en dimensiones más profundas del hueco del conejo. Para conocer si nuestra estructura es arriostrada debemos saber cuánto se deforma lateralmente producto del estado de cargas que estamos considerando. En el cálculo de estas deformaciones debemos considerar preferentemente situaciones de carga lateral aplicada a la estructura y rigideces fisuradas iniciales de los elementos.
Las rigideces en el cálculo de deformaciones laterales aplicadas al pórtico estarán en el más simple de los casos en función a:
A partir de estas inercias fisuradas iniciales podemos calcular el arriostramiento de la estructura en función a dos parámetros. El factor de estabilidad Q o incremento de Momentos en columnas producto de P-Δ.
a) Si P-Δ incrementa los momentos en los extremos de la columna en más de 5%, la columna es No Arriostrada. Caso contrario es Arriostrada
b) Si Q excede 0.05, el piso es Arriostrado. De otra manera el piso en análisis es No Arriostrado. Q está en función de
Una vez definida la situación de arriostramiento para la columna en análisis se puede obtener k en función al ábaco propuesto por el ábaco del comentario ACI318-19 R6.2.5.1 que se muestra a continuación:
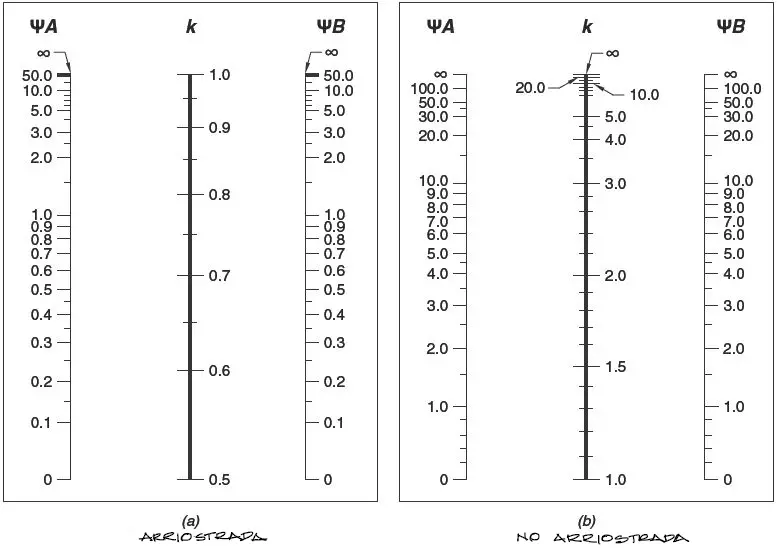
Los factores ΨA y ΨB se calculan como la división entre la suma de las rigideces Σ(EI/Lc) de las columnas en el nudo entre la suma Σ(EI/L) de las vigas. El procedimiento se repite para los dos extremos A y B de la columna.
Rigidez Efectiva (EI)eff
El paso para calcular Pc consiste en conocer (EI)eff. La norma ACI propone varias fórmulas en su artículo 6.6.4.4.4 sin embargo la más sencilla de calcular de todas ellas es la mostrada a continuación:
Últimas consideraciones
Este procedimiento debe repetirse en las dos direcciones de ejes principales de la sección de la columna.
El procedimiento puede parecer largo, sin embargo si se programa en una planilla de cálculo, solo se necesitan como datos las medidas de la sección transversal, y las solicitaciones en los extremos de la columna.
Siguiente paso
Con el momento Mc de diseño obtenido, junto con la carga axial Pu mayorada, se deben introducir ambos datos a algún programa de cálculo de aceros mediante diagramas de interacción, donde la solicitación (Mc,Pu) no debe ser mayor que la curva de diseño del diagrama de interacción.
Cuento en esta página web con un programa en línea que te puede ayudar a calcular el diagrama de interacción de manera rápida en:
Diagrama de Interacción para columnas rectangulares con Acero en las cuatro caras
Ejemplo
Para tener un panorama más claro del diseño de columnas por pandeo, elaboré en el siguiente artículo un ejemplo referente al diseño de columnas sometidas a pandeo.
– EJEMPLO DE COLUMNA ESBELTA DE HORMIGÓN ARMADO
autor: Marcelo Pardo
Buenas noches me gustaría saber como resuelvo este tipo de ejercicios, entiendo que es una columna que esta empotrada en la base y libre en su extremo superior.
ejercicio:
Considere la columna en volado, para las cargas axiales: 0, 0.1Agf´c,0.2Agf´c ,0.3Agf´c,0.6Agf´c . Ag: Área bruta de la sección. Estime la máxima capacidad de desplazamiento lateral de la columna.
James, para tal propósito debes realizar el procedimiento estableciendo K = 2 y siguiendo de igual manera los pasos del ejemplo de columnas esbeltas del enlace de esta publicación
Gracias Marcelo, por tu pronta respuesta a mi observación respecto a la división de los dos momentos M1/M2. En realidad me refería a que la redacción del párrafo concordara con lo indicado en los croquis.
Gracias, Saludos
Alberto Porras López
Oh ya entiendo!! Ahora mismo :)! gracias nuevamente
Estimado Marcelo: Una observación:
En la sección que dice:
M1 = momento más pequeño en un extremo de la columna
M2 = momento más grande en el otro extremo de la columna
La división de estos dos momentos M1/M2 será positiva cuando formen una curvatura doble en la columna, y positiva cuando se produzca una curvatura doble:
creo que debe corregirse la última parte del párrafo diciendo: «…y NEGATIVA cuando se produzca una curvatura SIMPLE»
Saludos
Alberto Porras López
Alberto buenas tardes: Dejame revisarlo. Ha habido una confusión grande respecto a esa división justamente porque hay un cambio de signos dependiendo del año de la norma. Claro que el resultado final es el mismo independientemente de la norma que que aplique. Pero lo revisaré
Que tal ingeniero, excelente aporte, solo me queda una duda, en la fórmula de M nos indica que M=Mns+$sMs dónde:
Mns=momentos producto de cargas verticales
Ms=momentos producto de cargas horizontales
Suponiendo que estoy haciendo el cálculo a mano, quiero entender que cargo un pórtico con cargas verticales y lo resuelvo (saco el momento), después cargo el mismo pórtico pero ahora con cargas horizontales y lo resuelvo (saco el momento el cuál multiplicó por $s), después esos 2 momentos los sumo y el resultado me da el momento de segundo orden ¿Cierto? Pero entonces mi duda es, Pdelta (momento de segundo orden) en si NO se calcula? Es decir no podemos agarrar P del marco con cargas verticales y multiplicar por el delta del pórtico que tiene cargas horizontales?????
MARCELO: graves problemas para calcular el factor de estabilidad Q , sin poseer un programa de calculo estructural, dado la dificultad de poder establecer los valores de la sumatoria de las Pu y los desplazamientos horizontales de los nudos en forma espacial, o sea considerando la totalidad de la estructura en sus tres ejes en la planta o nivel en que se encuentra el pórtico estudiado, gracias.
Jorge buenas tardes. No entiendo exactamente a qué te refieres? no tienes un programa de cálculo estructural?
Muy bien explicado ing. Yo tengo una duda en particular, tengo un caso en el q varias columnas esquineras y centradoras son de 25×25 con 4 fierros 3/8 y se quiere elevar dos losas,
Si no se cumplen cuantias q pasaria con la estructura?
Ya se verifico con el diagrama de iteraccion …
Muchas gracias Ing Marcelo Pardo por la explicacion.
Tengo una pregunta sobre columnas.. q pasa si no se cumplen cuantias desde el principio? Es decir, que una columna haya sido construida con 4 fierros 3/8 siendo 25cm x 25 cm su dimencion, y el cliente quiere elevar pisos. ???
Ya verifique a flexocompresion y a pandeo como enseño usted, aunque tengo duda sobre rl Pdelta.
Si las columnas no cumplen con las resistencias y el dueño quiere seguir construyendo, se le indica la situación y se le hace firmar un documento de deslide de responsabilidades del ingeniero.
El Cm mayor o igual a 0.4, solo no especifica este aspecto como tal la norma en el apartado 6.6.4.5.3 a que se debe de que el valor de Cm debe estar en un valor entre 0.4 y 1?
Stefanie, francamente no sabría responderte por qué.
Es una explicación genial de este fenómeno de la Esbeltez, el cual en algunas universidades se le da bastante de lado. Pero tengo una duda, he diseñado algunas columnas con programas como el tekla structural designer, cype, staadpro y no veo que tomen en cuenta el % que se incrementa el momento total(incluyendo el p delta)con relación al momento obtenido por análisis lineal. Según la norma ACI no lo puede sobrepasar en más del 40%. Agradezco cualquier aclaración al respecto porque en los ejercicios que he encontrado resueltos no se da ese caso.
Ariel que tal!! Bueno, si tienes un incremento de 40% respecto al momento original es porque de hecho tu columna tiene un Delta demasiado grande. En cuyo caso se debe rigidizar la estructura lateralmente. Francamente no recordaba ese aspecto del incremento de 40%, me vas a hacer revisar nuevamente la norma. jeje! Muchas gracias!
Muy bien explicado y complementado con el ejemplo del link facilitan una mejor comprensión del tema que de por si es bastante complejo, muchas gracias por compartir sus conocimientos, es un excelente material de apoyo.
GRacias Luis. Debo mencionar que en el ejemplo se asume el factor K como 1. A tomar muy en cuenta que este factor puede ser un poco mayor si el pórtico no está arriostrado
Tal vez un ejemplo de hallar el valor de k de un portico, el arriostramiento o el no arriostramiento seria genial ing.
De hecho David, es lo siguiente que quiero escribir