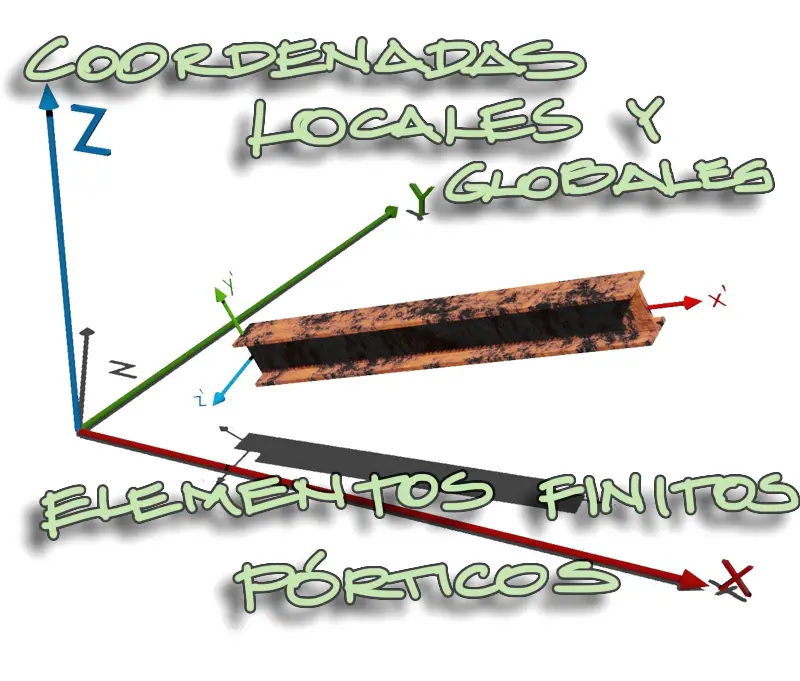
Coordenadas locales y globales
Se vió en una anterior publicación la expresión matricial de la matriz de rigidez de un elemento de barrasometido a todas las solicitaciones posibles en 3 dimensiones. Este es el enlace al artículo de la Matriz de Rigidez de Barra en 3D.
Sin embargo, como se mencionó en dicha publicación, la matriz de rigidez mencionada está alineada con los ejes locales de la barra, donde x’ coincide con el eje longitudinal de la barra, y’ es el eje vertical de lasección transversal y z’ el eje horizontal de la sección transversal:
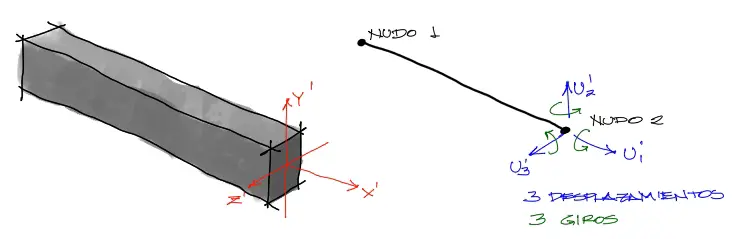
El problema es que estos grados de libertad de la barra, deben estar orientados en coordenadas globales para poder ensamblarse con otros elementos adyacentes, que también deban estar en coordenadas globales. Para transformar las coordenadas locales de la matriz de rigidez a coordenadas globales, una alternativa fácil de comprender es realizar ciertas rotaciones en el orden que se menciona en este artículo.
El eje Z global representa la altura
La bibliografía orienta siempre el eje local y’ de la barra en el sentido vertical de su sección transversal como en la imagen siguiente:
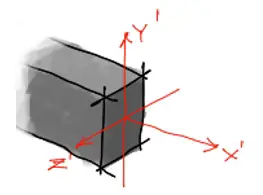
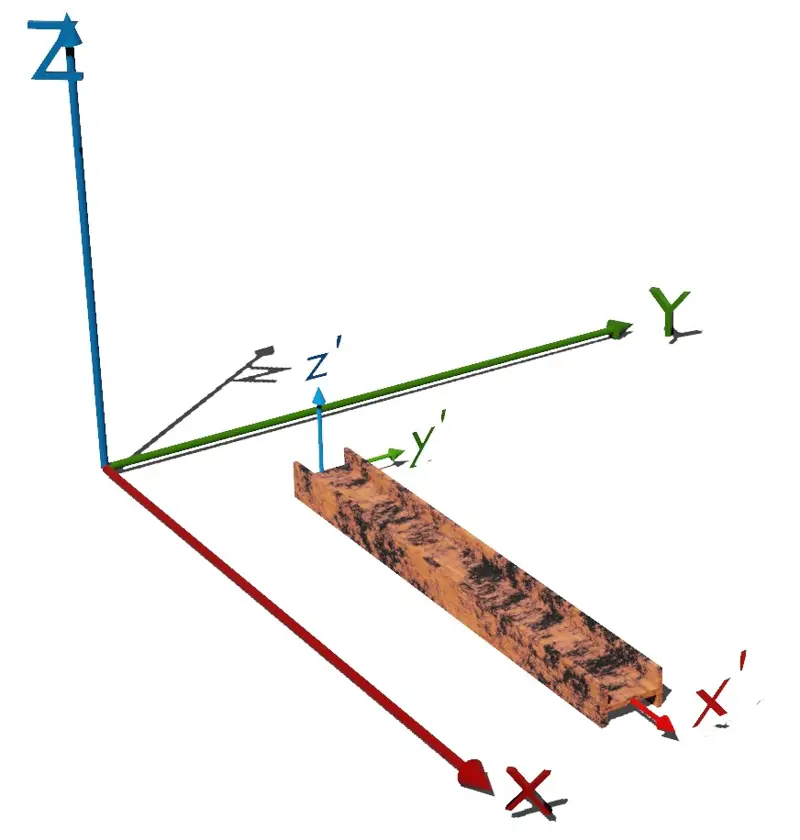
Sin embargo en el modelado de estructuras en 3 dimensiones el eje Z global es el que suele representar la altura de los modelos.
A partir de este razonamiento, el elemento de barra con coordenadas locales x’y’z’ sin ninguna rotación representado sobre un sistema de coordenadas global XYZ se ve como en la siguiente figura:
Rotaciones mínimas del elemento
El número máximo de rotaciones necesarias para lograr que un elemento termine en su posición final a partir de una posición local son 3.
– rotación del elemento de barra respecto a su propio eje (“roll”).
– rotación respecto al eje horizontal perpendicular al eje (rotación de cabeceo o elevación “pitch”)
– rotación respecto al eje vertical (rotación de base o de derrape “yaw”)
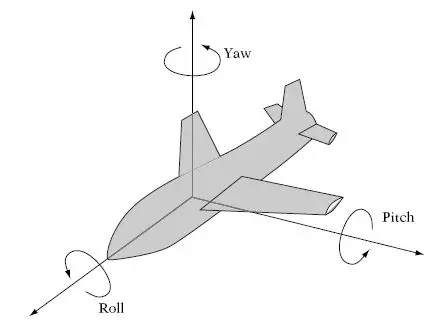
Aplicaremos estos mismos conceptos a la rotación de nuestro elemento de barra, en el orden mencionado
Rotación del elemento de barra respecto a su eje
Lo primero que debemos hacer para acomodar el elemento de barra a una posición donde la altura de la sección transversal de la viga esté vertical es aprender a rotarlo respecto de su eje.
Como se pudo ver en la anterior imagen, la barra sin aplicar ninguna rotación, se encuentra echada respecto a un sistema coordenado global donde el eje Z representa la altura. Entonces para rotar el elemento y matemáticamente su matriz de rigidez, debemos aplicar el siguiente proceso.
Denotamos primeramente con α el ángulo de rotación de la barra respecto a su eje. Este ángulo se verá así durante el proceso de rotación:
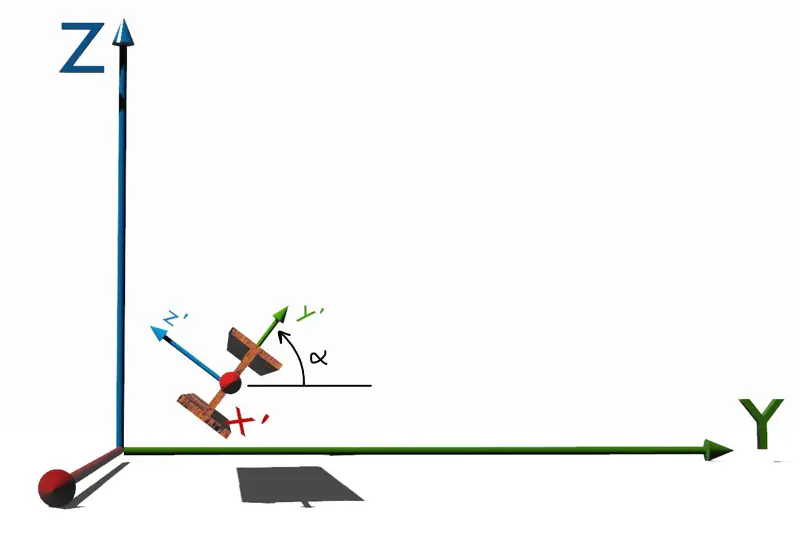
Matemáticamente esto conlleva la rotación de ejes a partir de una matriz de rotación con cosenos directores. Cuando rotamos la matriz de rigidez local mencionada en el anterior artículo que de ahora en adelante llamaremos [K_local], la matriz de rigidez rotada que llamaremos [K_eje] toma la siguiente expresión:
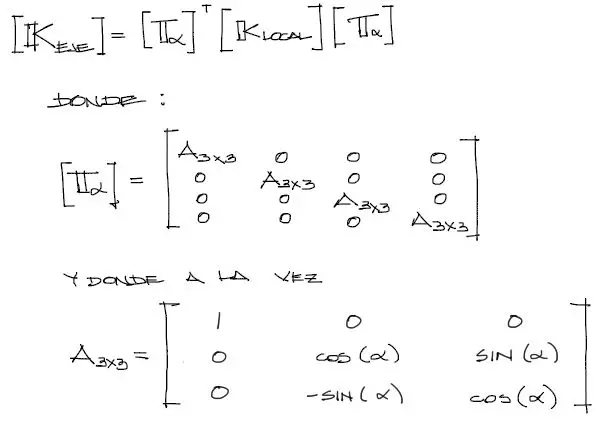
En la expresión mostrada, la matriz de transformación Tα es una matriz 12×12, que tiene la misma dimensión que K_local. A la vez, la matriz [Tα] está compuesta por submatrices de 3×3 y los “ceros” de la matriz [Tα] son matrices de ceros de 3×3. Todo este concepto estará mucho más claro con un ejemplo demostrativo que escribiré más adelante.
Rotación de cabeceo o elevación del elemento
Una vez obtenida la posición final de rotación respecto al eje de la barra, procedemos con la rotación del elemento en el plano XZ global, o dicho de otra manera, respecto al eje Y global. El esquema de rotación buscado se grafica a continuación:
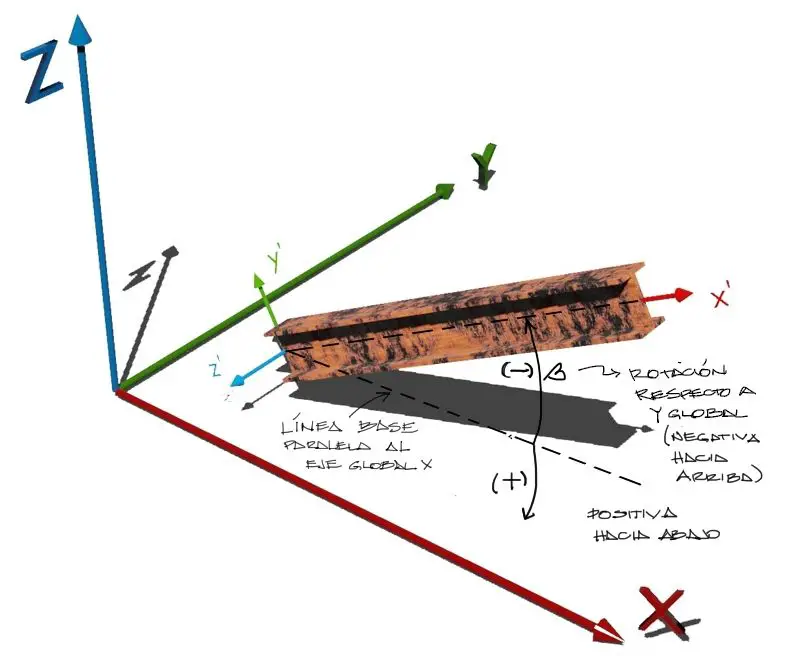
La matriz rotada sobre el plano XZ la llamaremos [K_altura] y la obtendremos a partir de una transformación de rotación aplicada a la matriz [K_eje] del anterior subtítulo. El ángulo de rotación sobre XZ en sentido antihorario positivo lo hemos llamado “β” por tanto la matriz de rotación la denominaremos [Tβ]. La expresión de rotación en este caso será:
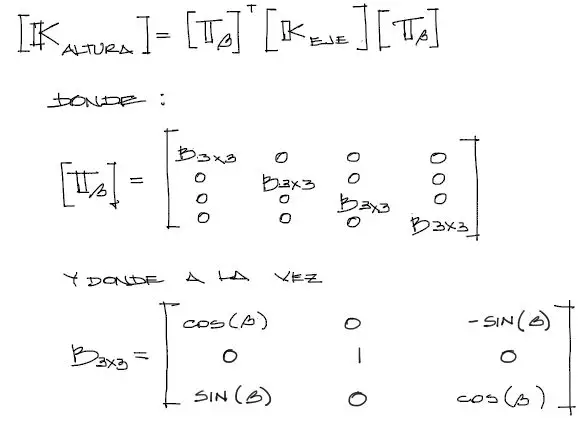
Debemos notar que el sentido de rotación antihorario positivo se dirige en dirección “hacia abajo” medido desde el plano XY. Esto se debe a que el giro sobre el eje Y barre en dirección positiva partiendo siempre del eje Z positivo en dirección del eje X positivo, por la regla de la mano derecha. En ese mismo orden de razonamiento, el ángulo β negativo rotará la viga “hacia arriba”.
Rotación respecto al eje Z sobre el plano XY (rotación de derrape)
Finalmente la rotación de derrape o rotación sobre el plano XY del elemento nos permitirá obtener la posición del elemento de pórtico en 3 dimensiones.
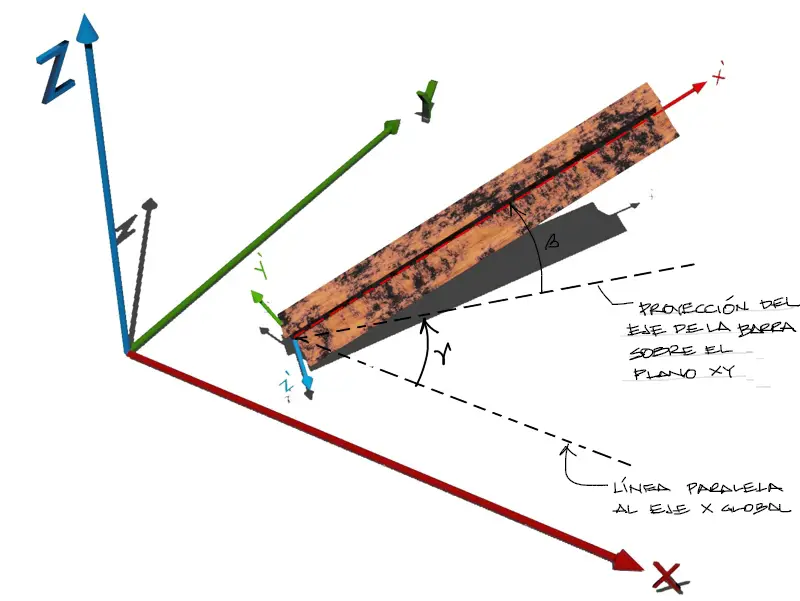
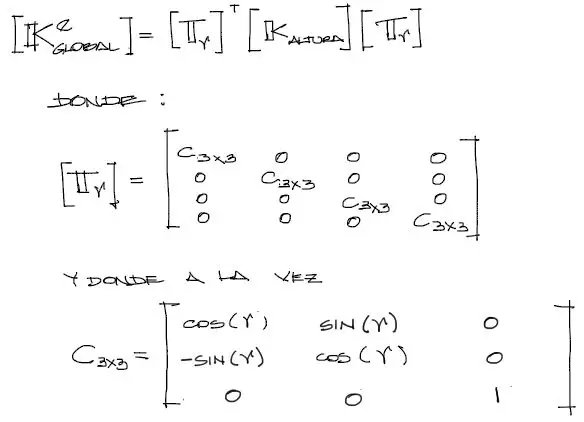
Llamaremos “gamma” o “ɤ” al ángulo de rotación en el plano XY o respecto al eje global Z. Luego, a la matriz rotada respecto al plano XZ anterior [K_altura] le aplicaremos una matriz de transformación de rotación que llamaremos [Tɤ] y la matriz elemental final rotada en su posición final obtenida la llamaremos [Ke_global] (denotando Matriz de rigidez “K” de un elemento “e” en coordenadas globales.)
La expresión matemática de la rotación de [K_base] a [Ke_global] es entonces:
Aplicar las 3 rotaciones simultaneamente
Si se quiere, se pueden aplicar las tres rotaciones simultaneamente sobre la matriz de rigidez local, pero en el mismo orden explicado arriba. Entonces la fórmula de rotación de coordenadas locales a globales en una sola operación será:
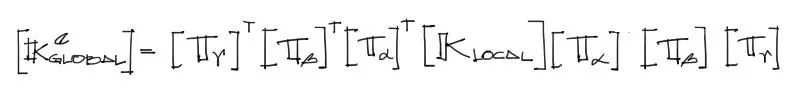
Qué sigue?
El siguiente paso es el ensamblaje de cada elemento hacia una matriz de rigidez global de toda la estructura. Sin embargo eso se verá más adelante.
Bibliografía
Los conceptos básicos de rotación de las matrices de rigidez en 3d se puede consultar en la bibliografía:
– A first course in the finite element method – Daryl Morgan (pag. 257)
– Matrix structural analysis – McGuire (pag. 95)
autor: Marcelo Pardo
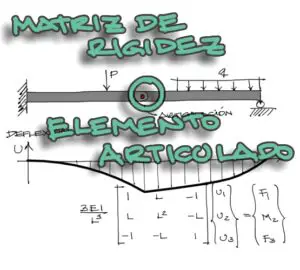
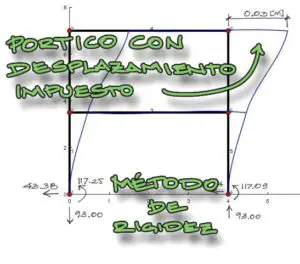
Excelente contenido ingeniero, una observacional en el tercer párrafo, tercera linea existe un error. Ahí dice “decomprender” . Saludos desde Quito Ecuador
Muchas gracias! lo corrijo ahora mismo! 🙂