
Planteamiento del problema
Hace algún tiempo hablé acerca de la matriz de pórticos en 3 dimensiones y además acerca de la rotación de los elementos en 3d para su respectivo ensamblaje en la matriz de rigidez.
Realizado este paso, el procedimiento matemático para la resolución de pórticos en 3 dimensiones es muy similar al de pórticos en 2 dimensiones.
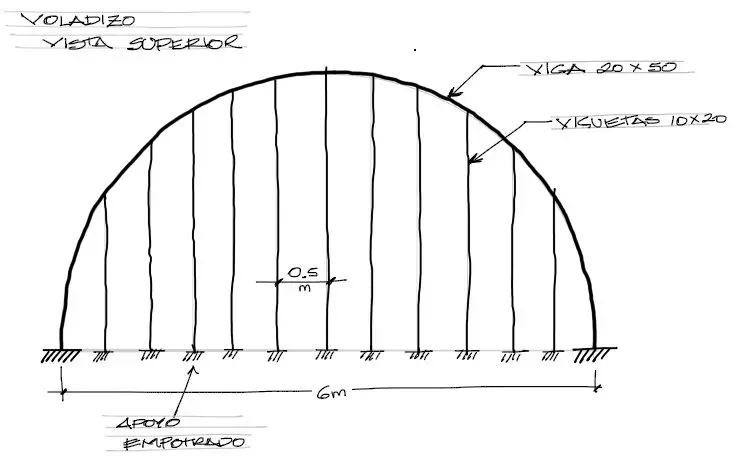
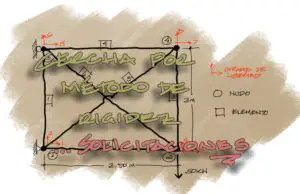
Para mostrar el proceso de cálculo, vamos a pantear el cálculo de las solicitaciones de una viga circular en voladizo como la mostrada en la siguiente imagen:

Las secciones de la viga serán de 25×50 centímetros y para las viguetas una sección de 10×20. Además la viga proyecta un semicírculo perfecto de radio de 3 metros.
Planteamiento de elementos de barra
El primer paso como en todo cálculo consiste en la numeración de nudos y barras, así como la ubicación coordenada de dichos nudos y barras. En este caso seguiremos el siguiente orden:
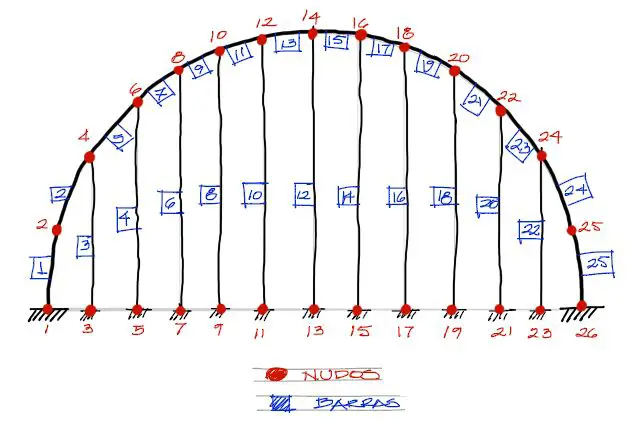
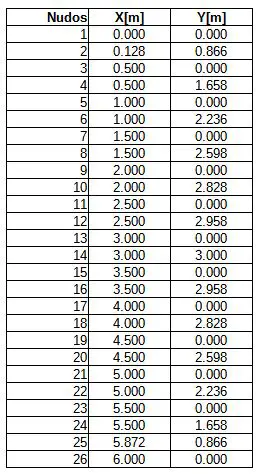
Se sobre entiende que los tramos de barra son todos rectos (lograr elementos subparamétricos curvos de barra sería demasiado complicado y fuera de los alcances de este artículo). Para lograr una emulación de tramo curvo entre los nudos 1 y 4 se decidió colocar un nudo intermedio. Lo mismo sucede con el nudo 25. Exceptuando estos dos nudos, todos los nudos están separados 0.5m horizontalmente. Las coordenadas de estos nudos son:
Datos de longitud y ángulo de cada barra
Como se vio en la teoría de matrices de rigidez en 3D, necesitamos varios datos de cada barra para armar su matriz de rigidez en coordenadas locales y posteriormente la matriz rotada en su posición final.
Comencemos por los datos de longitud y de ángulo de rotación de las barras. La longitud de cada barra puede obtenerse fácilmente a partir de las coordenadas de nudo de inicio y nudo final de cada barra. Para una barra como la barra 7 por ejemplo, con nudos de inicio 6 y fin 8, tenemos:
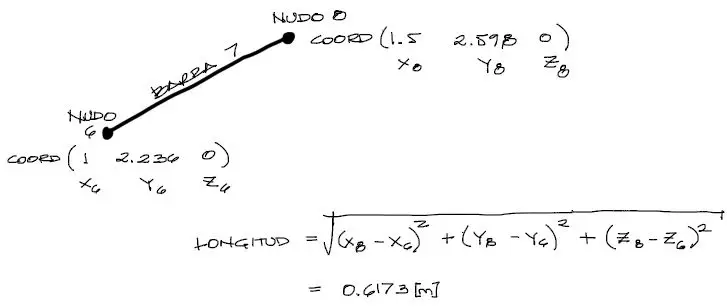
A partir de la longitud conocida del elemento, podemos obtener el ángulo de rotación en el plano XY del elemento a partir de la siguiente expresión:
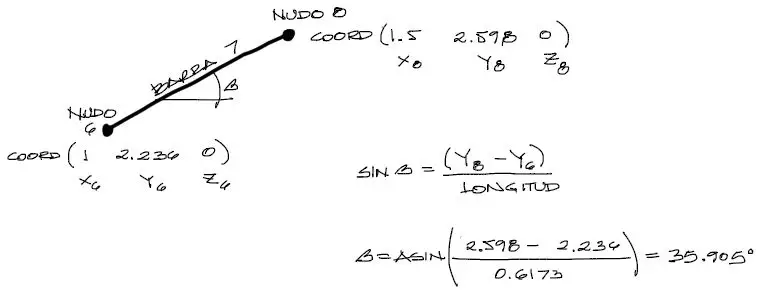
Llamamos ɤ al ángulo de giro en el plano XY (el tercero de los giros de coordenadas locales a globales), consecuentes con el nombre que le dimos a los giros de cada elemento en el artículo de Rotación de elemento de barra para pórtico en 3D.
Para el resto de los elementos se procede exactamente de la misma manera. Ordenando los datos en una tabla resulta:
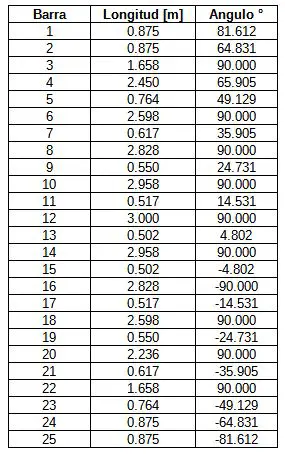
Datos mecánicos de sección de cada barra
Las propiedades de sección de las barras involucradas se orientan a partir de un plano local de la sección transversal x’y’, tal como lo explica la teoría de Matriz de rigidez de elemento de barra en 3D
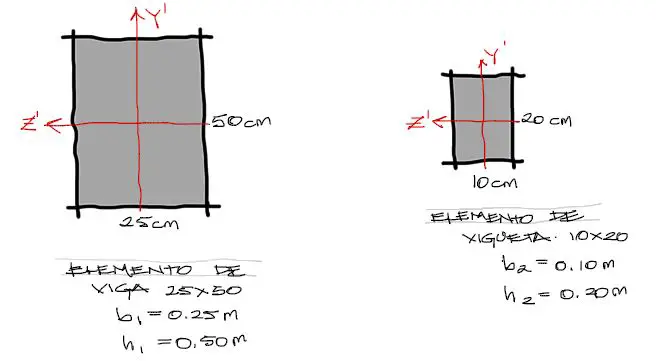
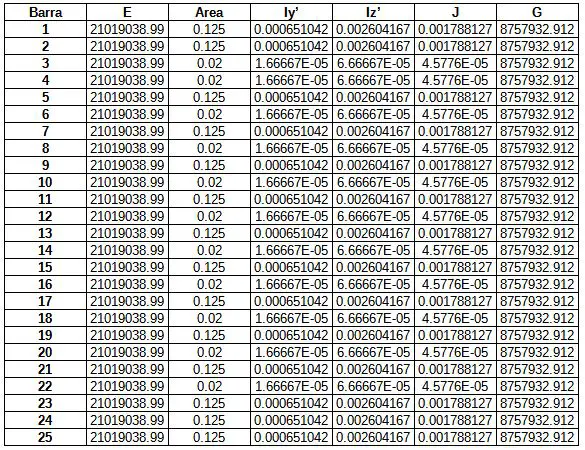
Para los datos expuestos, las propiedades de sección necesarias de cada elemento de viga o vigueta son:
– área
– Inercia Iy’
– Inercia Iz’
– Módulo de torsión J
– Módulo elástico E
– Módulo de corte G
Se pueden obtener todos los datos enumerados, excepto E y G. Para obtener estos datos partiremos de la fórmula planteada por la ACI318-19 para un concreto de 20MPa de resistencia característica (la resistencia más común que existe) y además un módulo de poisson del concreto de v=0.20.
Entonces se tiene para el elemento de viga:
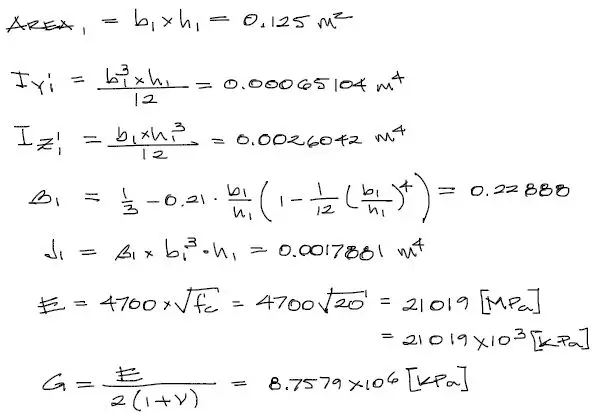
Como puede observarse, tanto módulo elástico E como de corte G se calculan en KPa, debido a que como se verá más adelante, estas son las unidades de fuerza y esfuerzo más cómodas de manejar (ya que las cargas se manejan en unidades de [KN]). De la misma manera se procede para el elemento de vigueta.
Ordeando todas las propiedaes mecánicas de cada barra, obtenemos los siguientes resultados:
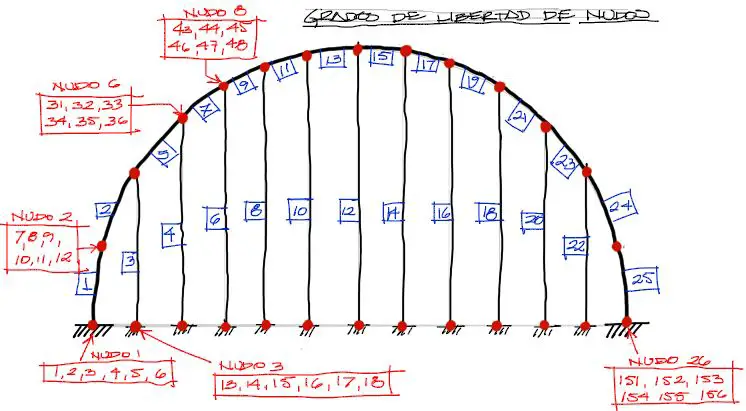
Grados de libertad
Cada barra tiene dos nudos. un nudo de «arranque» y uno de «llegada». cada uno de estos nudos tiene 6 grados de libertad que deben estar bien definidos al momento de conocer las conexiones entre elementos. Si vamos numerando 6 grados de libertad por nudo (tres desplazamientos en x y z y tres giros en x y z) tendremos algo así:
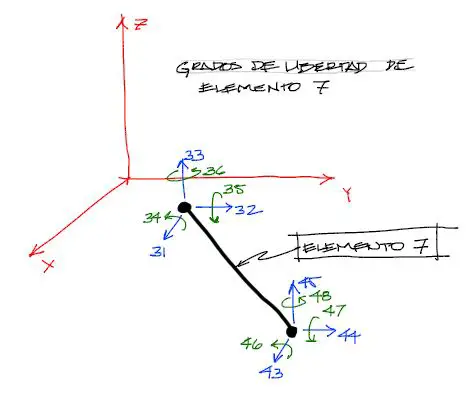
En particular hemos dado especial importancia al elemento 7 desde el comienzo, y para este elemento los grados de libertad se verían más o menos así en el sistema coordenado global:
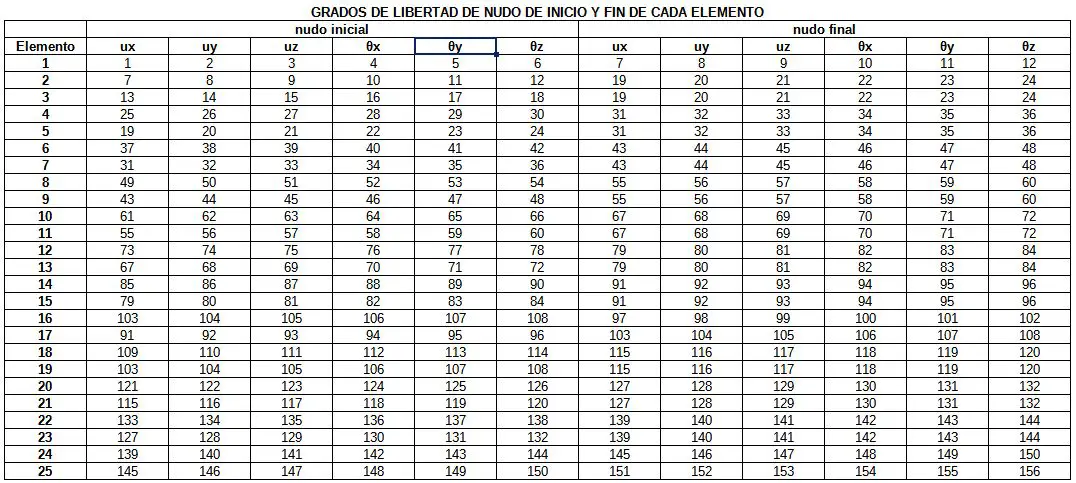
Los grados de libertad de todos los elementos se pueden ordenar en la siguiente tabla, que nos será muy útil al momento de ensamblar todos los elementos dentro de la matriz de rigidez global de 156×156.
Matrices de rigidez local
Debemos crear una matriz de rigidez local para cada elemento de este ejercicio. La matriz en coordenadas locales (como mencioné en la Teoría) es la siguiente:
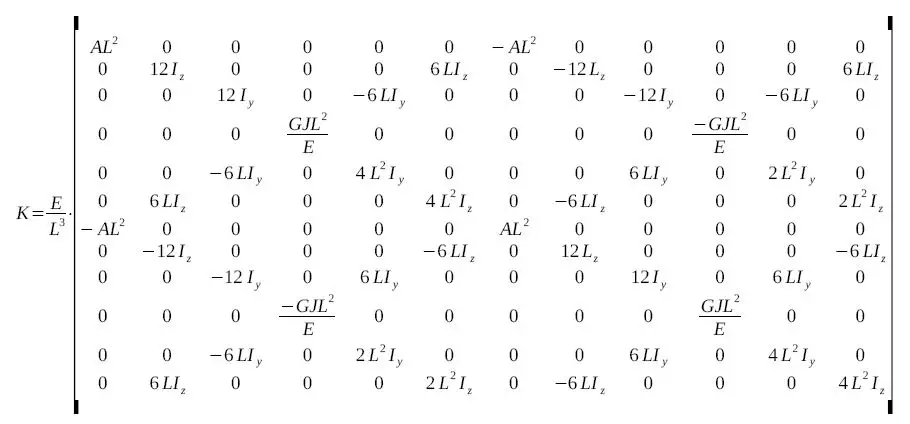
Luego se hace el reemplazo directo para cada elemento. Para este caso tomaremos como ejemplo el elemento de barra 7. Haciendo el reemplazo de todas las variables:
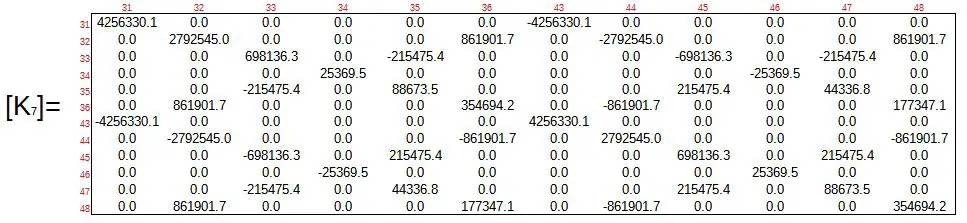
El procedimiento repetitivo es el mismo para todas las otras barras. Se debe notar como imaginariamente es buena práctica enumerar los grados de libertad de arranque y llegada encima y al costado de cada matriz de rigidez local. Esto nos ayuda a entender qué posición toma cada elemento de la matriz local dentro de la matriz global que ensamblaremos luego, de dimensión 156×156.
Matrices de rigidez local para descargar
Se pueden descargar las matrices de rigidez de cada elemento en el siguiente enlace:
Matrices elementales en coordenadas locales.zip
Qué sigue:
Para no hacer la publicación muy larga, vamos separarla en secciones. En la SIGUIENTE PUBLICACIÓN vamos a encontrar las matrices de cada elemento en coordenadas globales y finalmente ensamblar la matriz de rigidez global.
autor: Marcelo Pardo


Saludos masestro, estoy revisando la publicacion y re-escribiendolo en excel y revisando la longuitud de la barra #4 y su respetivo angulo difiere de los obtenidos por mi siendo mis resultados de 2.3600 m para la barra #4 con un angulo de 90 grados, podria revisarlo por favor? gracias y espero poder seguir disfrutando de su contenido.
Luis, muchas gracias por la observación. Lo revisaré