Enunciado

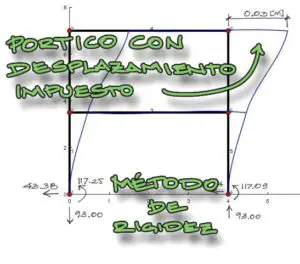
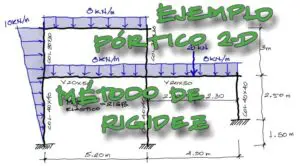
Se pide encontrar las solicitaciones de momento flector, cortante y axial del siguiente pórtico hiperestático:

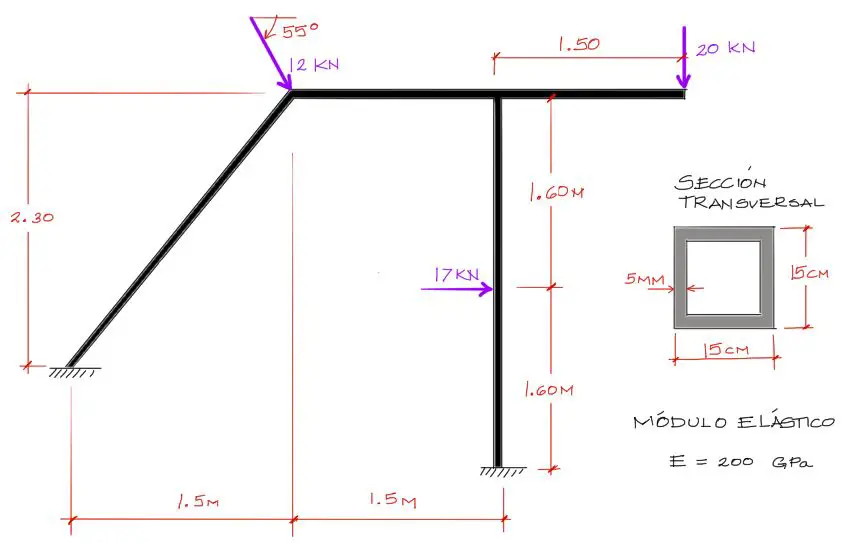
La numeración de nudos, grados de libertad y barras se muestran a continuación:

Los resultados de desplazamientos de los nudos producto del análisis Estático por el método de rigidez son los siguientes:

Pasos previos

Para llegar a los desplazamientos de los nudos mostrados en el enunciado se siguió un procedimiento de resolución mediante el método de rigidez. Esta resolución la encuentras en el enlace siguiente
→→→ Resolución de pórtico con cargas puntuales por método de rigidez

En este artículo se aplican conocimientos de matrices de rigidez elementales y globales que utilizaremos también en este artículo.

Posproceso

Suelo llamar “POSTPROCESO” a todo el cálculo de solicitaciones posteriores al cálculo de desplazamientos y reacciones. Esto se debe a que concretamente el método de rigidez para encontrar los resultados del problema termina en el anterior artículo mencionado. A partir de aquí aplicamos simplemente conocimientos de resistencia de materiales y de equilibrio estructural para encontrar las solicitaciones en cada barra.

Coordenadas locales

Los desplazamientos encontrados en toda la resolución del anterior artículo corresponden a desplazamientos de los nudos en coordenadas globales. El primer paso para conocer las solicitaciones de cada barra es transformar estos desplazamientos globales en desplazamientos locales alineados con el eje de la barra, de la siguiente manera. Por ejemplo para la barra 1:

Si bien las barras 2 y 3 no necesitan tal transformación pues su eje coincide con el eje de las X y por tanto los desplazamientos en coordenadas locales coinciden con las globales. Por tanto aplicaremos la transformación a ejes locales para las barras 1, 4 y 5.

Para lograr esta transformación de coordenadas se debe aplicar la matriz de rotación T utilizada en el anterior artículo y en la TEORÍA DE MATRIZ DE RIGIDEZ DE PÓRTICO EN 2D.

La transformación de coordenadas globales a coordenadas locales se ejecuta entonces de la siguiente manera:

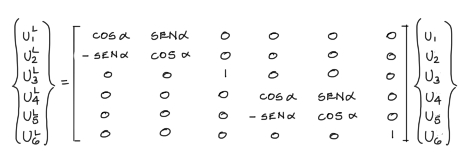
Aplicado al elemento 1 (y a todos los otros elementos en general) se obtiene:

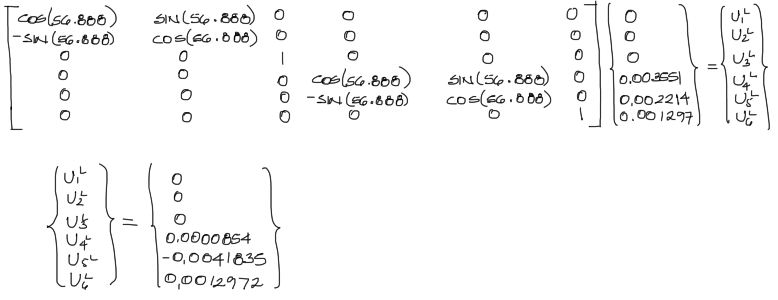
Por ejemplo para el elemento 1, una vez ejecutada la rotación de los desplazamientos, el elemento queda como en la siguiente imagen. Se puede a partir de la siguiente imagen, determinar cuales de los desplazamientos generan compresión en la barra, y cuales de los desplazamientos generan flexión y cortante.

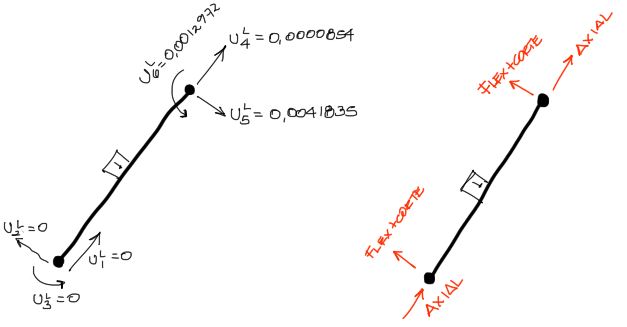
Habiendo desacoplado los desplazamientos separándolos entre los efectos que generan deformación axial y los que generan deformación por cortante y flexión, se puede determinar cual es la solicitación axial de la barra y cuales son las solicitaciones de cortante y flexión.

Solicitación axial

A partir de conceptos de resistencia de materiales, se puede determinar si la barra está a compresión o a tracción en base a la diferencia de desplazamientos axiales u1 local y u4 local. Además como la diferencia de ambos desplazamientos es la deformación, y dividiendo ésta entre la longitud obtenemos la deformación unitaria, entonces:

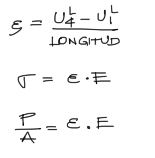
De las fórmulas arriba, el esfuerzo axial es por definición igual a la deformación unitaria por el módulo elástico, y además el esfuerzo axial se descompone en Fuerza Axial entre la Sección transversal. Por tanto despejando la fuerza Axial P se obtiene la fórmula de solicitación axial de la barra:

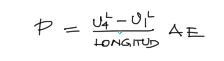
Reemplazando los datos para este elemento, se obtiene la solicitación para la barra. nota que el signo del resultado automáticamente denota si la barra está a compresión (signo negativo) o si está a tracción (signo positivo). Además las unidades de los valores introducidos a la fórmula son, u1 y u4 en [m], Area en [m²], E en [KN/m²], Longitud de la barra en [m].

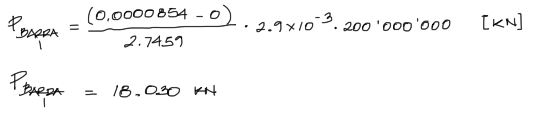
Repetimos el mismo procedimiento para todas las otras barras. Sin excepción el proceso es idéntico. Obtenemos entonces el resultado siguiente para las otras barras, y graficamos los resultados.

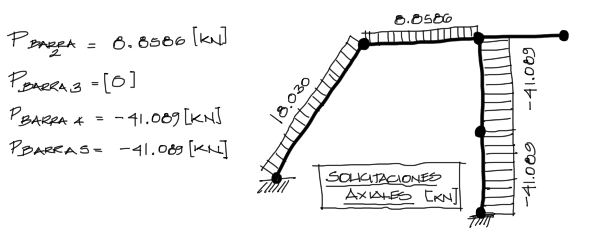
Solicitaciones de Momento Flector y Cortante

Para conocer las solicitaciones de Momento y Cortante de las barras continuamos trabajando con los desplazamientos en coordenadas locales de cada barra.

De los 6 desplazamientos en coordenadas locales, desechamos los desplazamientos axiales que se utilizaron en el anterior apartado. Analizamos entonces los desplazamientos locales u2, u3, u5 y u6.

En el artículo CORTANTES Y MOMENTOS FLECTORES A PARTIR DE DESPLAZAMIENTOS desarrollado para solicitaciones en vigas se explica como obtener M y V a partir de estos desplazamientos. Se utilizará esta misma teoría para las barras de pórticos.

En este procedimiento mencionado los desplazamientos perpendiculares a la barra son U1 y U3, que nosotros reemplazaremos por los desplazamientos locales u2 y u5. De la misma manera los desplazamientos de la teoría U2 y U4 los reemplazaremos por las rotaciones locales u3 y u6. Queda entonces:

En el sistema de ecuaciones mostrado existen variables que para el caso de las barras analizadas en coordenadas locales valen X1=0 y X2=longitud de la barra. Los coeficientes A y B para este ejercicio son cero ya que las cargas distribuidas son nulas.

Las constantes C1 C2 C3 y C4 obtenidas corresponden a las constantes de integración de la ecuación de la elástica que sirve para encontrar los coeficientes del polinomio de las ecuaciones de cortante y Momento flector. Necesitas ver el vídeo de Solicitaciones de M y V a partir de Desplazamientos para entender mejor este concepto.

En resumen, el cortante y momento flector responden a las siguientes ecuaciones:

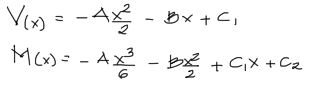
M y V Barra 1

Trabajamos con los desplazamientos locales de la barra 1, donde A=0 y B=0 porque no existen cargas distribuidas. Además x1=0 y x2=2.7459; A=0.0029m2; I=0.000010174m4; E=200e6. Reemplazando todos estos datos se obtienen las constantes:

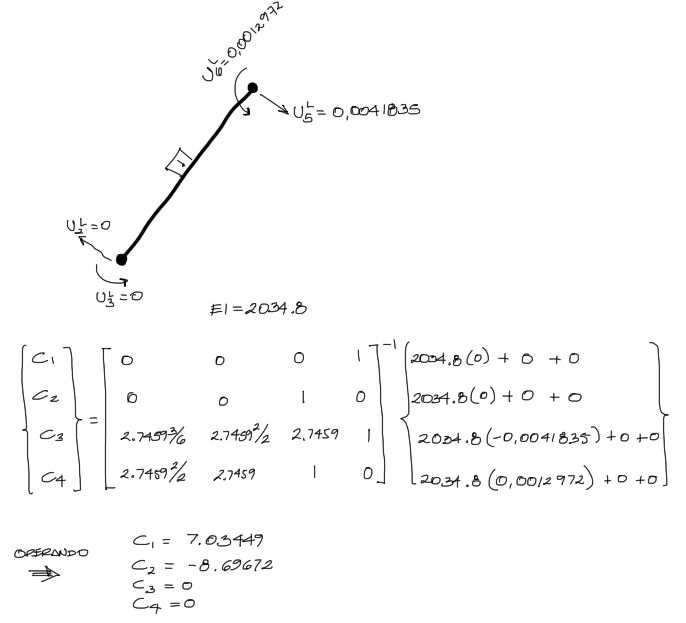
Estas constantes son los coeficientes de la ecuación de V y M:

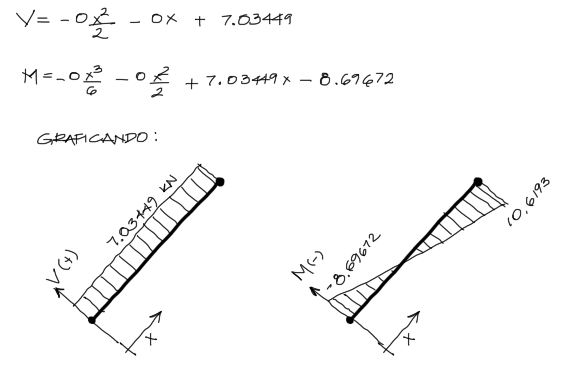
M y V para las demás barras

La única diferencia entre las otras barras y la barra analizada acá es que en las otras barras los desplazamientos del nudo 1 no son cero porque ya no estan empotrados. Por ejemplo para la barra 3:

Finalmente repitiendo el procedimiento para todas las otras barras y graficando:

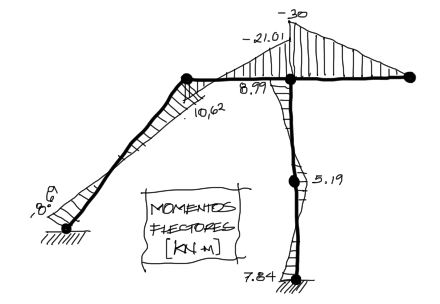
Con esto termina el procedimiento del análisis de solicitaciones del pórtico.

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS←←←