Pasos previos

En base a anteriores publicaciones, sabemos ya qué es la Cuantía balanceada y Cuantía máxima de una viga.

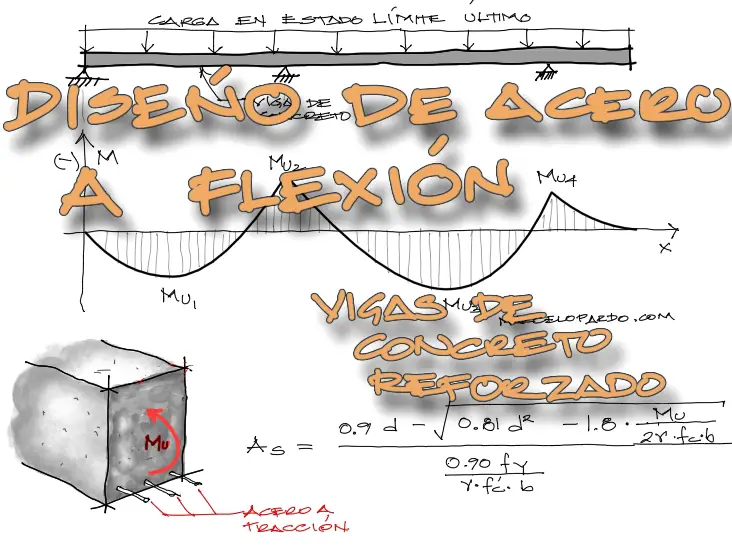
Como repaso, la cuantía balanceada es la cantidad de acero a tracción en la viga que logra que tanto acero como hormigón fallen al mismo tiempo. La cuantía máxima es la cantidad de acero que logra que este mismo acero falle un poquitín antes que el hormigón. En este sentido la cuantía máxima siempre será menor a la cuantía balanceada.

A partir de estos valores de cuantía (y de acero), podemos nosotros calcular cuanto momento flector puede resistir la viga con este acero máximo.

Este aspecto es importante porque el caso de diseño de vigas que analizaremos ahora se refiere a toda situación donde el momento solicitante Mu es menor que φMn-max

Datos del problema

Hasta ahora, todos los valores que obtuvimos de As-max, o φMn-max son propiedades de la sección transversal de la viga, que están en función a la geometría y resistencias de los materiales.

En otras palabras, hasta ahora no hemos hecho nada más que conocer el tope de acero a tracción que podemos ponerle a la viga sin que esta viga no necesite acero en la cara de compresión (situación que es poco deseable en todas las vigas).

Ahora estamos listos para utilizar las solicitaciones a flexión de la viga en análisis y obtener por fin la cantidad de acero que le corresponde a estas solicitaciones.

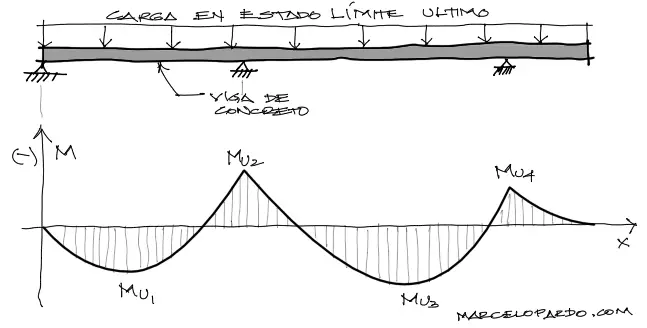En la mayoría de las vigas que se analizan, estamos en situaciones de varios momentos pico Mu1, Mu2, Mu3… etc. Para cada uno de estos momentos últimos vamos a diseñar o calcular la cantidad de acero necesaria para absorber estos momentos.

Caso de viga sin acero a compresión

Como mencionamos al comienzo del artículo, es siempre desable estar ante una situación donde no necesitemos acero en la cara de compresión de la viga. Cuando el concreto está muy solicitado a compresión y no es suficiente el concreto para resistir las solicitaciones por flexión, necesitamos de la ayuda de acero en esta zona. Esto conlleva a muy altos esfuerzos tanto en el concreto como el acero, y además es antieconómico.

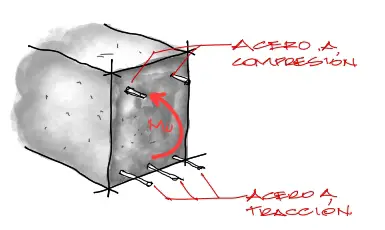Para lograr que la viga no lleve acero a compresión, debemos haber escogido una sección de viga tal, que el momento máximo φMn-max sea mayor a todos los momentos solicitantes en la viga.

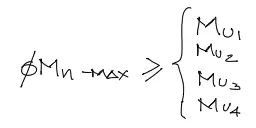Si no se diera el caso de que φMn-max sea mayor a todos los momentos solicitantes últimos, y se desea que la viga no lleve acero a compresión en ningún sector, existen tres alternativas:
– Aumentar la altura de la viga
– Aumentar el ancho de la viga
– Aumentar la resistencia del concreto

Entre las tres alternativas, generalmente la segunda suele ser la más factible, ya que por arquitectura es difícil aumentar el peralte de las vigas de manera desmedida, y aumentar la resistencia del concreto suele ser una alternativa muy costosa.

Deducción de fórmulas de diseño a flexión

El siguiente paso consiste en deducir la fórmula de diseño de sección de acero a partir de las fórmulas de equilibrio de la sección.

Como en todo análisis estático, debemos equilibrar tanto fuerzas como momentos de fuerza en el corte transversal de la viga:

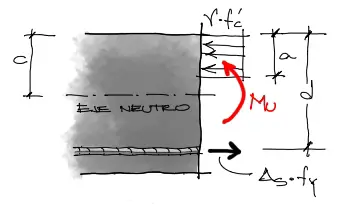Por sumatoria de fuerzas horizontales igualadas a cero, introducimos en la ecuación la resultante del bloque de compresión y la fuerza a tracción resultado del esfuerzo a fluencia del acero por su sección. En esta fórmula existen dos incógnitas. la altura del bloque de compresión “a” y la sección transversal del acero As (incógnita que finalmente es el objetivo mismo de este artículo).

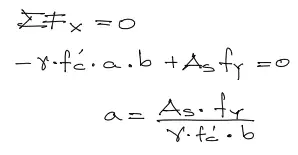Luego para aplicar la suma de momentos de fuerza localizaremos el pivote del sistema a la altura media del bloque de compresión de concreto, para que su resultante pase por el pivote y no genere brazo.

Luego haciendo suma de momentos respecto al pivote, la resistencia de la sección a momentos está dado sólo por la resultante de la fuerza del acero As•fy multiplicada por el brazo (d-a/2). Este momento de fuerza resistente por definición debe ser igual a la solicitación, por tanto:

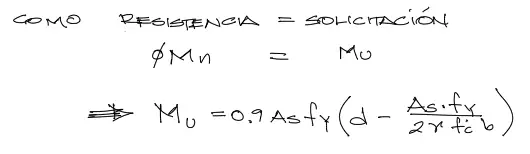Esta última es una ecuación de segundo grado donde la incógnita es As. La otra incógnita del sistema “a” ha sido anulada con la primera ecuación.

Resolución de la ecuación de segundo grado

El camino más adecuado para resolver esta ecuación de segundo grado es mediante la ecuación cuadrática:

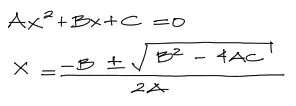Para aplicar esta fórmula debemos desarrollar la ecuación encontrada, despejando la variable “As” que es nuestra incógnita.

Luego todos los valores que acompañan la variable As son los coeficientes de nuestra ecuación cuadrática. Reemplazamos A, B, C dentro de la solución de la ecuación cuadrática:

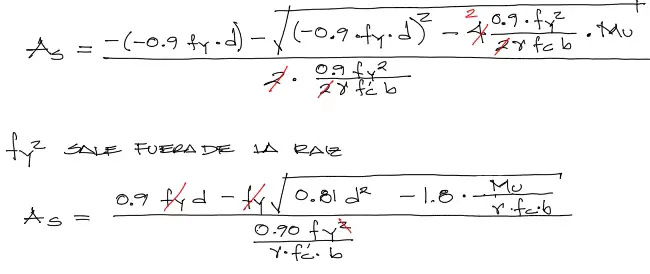De las dos soluciones positiva y negativa de esta ecuación, la que nos sirve es siempre la menor, correspondiente al signo negativo de la raiz. Se hacen luego las simplificaciones pertinentes y finalmente nos quedamos con la solución de la sección de acero en función al momento solicitante Mu.

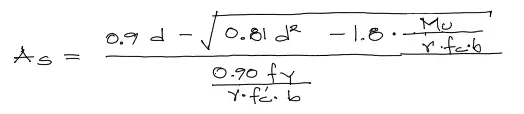Esta ecuación es la misma obtenida en el diagrama de flujo de cálculo de acero a flexión para vigas.

Consideraciones finales

Para la fórmula encontrada de As, debemos reemplazar Mu por cada uno de los momentos pico del diagrama de la viga, Mu1, Mu2, Mu3… etc. Además todas las unidades de esta fórmula deben ser consistentes. Es conveniente trabajar todo en [KN], [KPa], [m], [m2].

El Acero obtenido As luego deberá verificarse para que sea mayor al acero mínimo As-min en función a la fórmula:

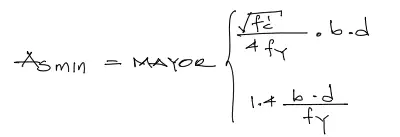Para entender todas las consideraciones del acero mínimo visitar: Acero mínimo a flexión. Se puede usar menos que As-min?

Esta sección de acero debe luego convertirse en barras de acero en función a las secciones de cada barra. Sumadas todas las secciones de las barras tentativas, su sección debe ser igual o ligeramente mayor a As. Para conocer la sección de barras puedes visitar:
– Diámetros y secciones de acero.
Para calcular de manera más sencilla la suma de secciones de cada barra, visita:
– Calculadora de secciones de acero de construcción

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE HORMIGÓN ARMADO ←←←