Enunciado

Dada la siguiente viga isostática,

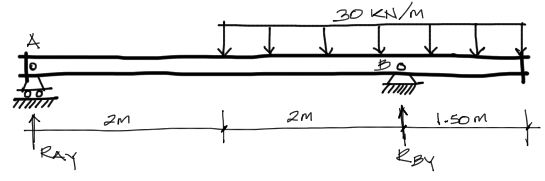
Resolver:
• Reacciones en los apoyos
• Ecuaciones de Momento flector y Cortante en cada tramo
• Dibujo de los diagramas de cortante y Momento flector de toda la viga

Solución

Equilibrio externo

En general cuando nos dan para resolver una viga de este tipo, siempre se piden las reacciones, momento flector y cortante, y las gráficas de estos diagramas. Es más, siempre se las pide en este orden, especialmente cuando se trata de vigas isostáticas.

Es por eso que comenzamos siempre con el equilibrio externo de la estructura. Para eso utilizamos las ecuaciones:

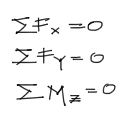
Podríamos comenzar por la sumatoria de fuerzas, pero como te habrás dado cuenta en ejercicios que hayas resuelto antes, las ecuaciones de sumatoria de fuerzas siempre tienen más de una incógnita. Para evitar esto, en el presente caso, aplicamos primero la sumatoria de momentos respecto del primer apoyo A:

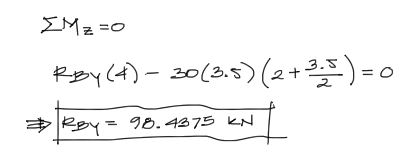
Y una vez conocida la reacción vertical en el apoyo 2 se puede conocer la reacción vertical en el apoyo 1, ahora sí con la sumatoria de fuerzas verticales igualada a cero:

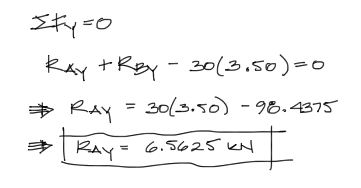
Equilibrio interno

Una vez conocidas las reacciones verticales, y teniendo presente que la reacción horizontal en el apoyo B es cero puesto que no existen fuerzas horizontales, se puede proceder a la obtención de momentos flectores y cortantes para cada tramo.

Para esto se realizarán cortes progresivos en la viga en puntos estratégicos donde se necesiten obtener las ecuaciones de momento flector y de cortante. Te darás cuenta dónde debes cortar cuando veas que existe un cambio del tipo de carga o un apoyo. Se hace el corte imaginario entonces entre cada cambio de carga o presencia de apoyo.

Realizando el primer corte imaginario en la viga en el tramo sin carga, se estabiliza el corte izquierdo de la viga con las ecuaciones de equilibiro. Comenzamos con la sumatoria de fuerzas verticales

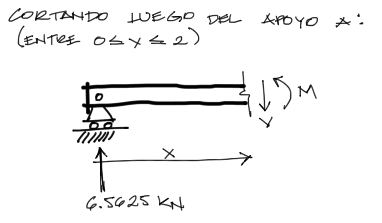
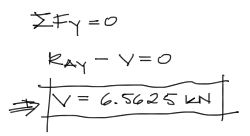
Luego, tomando como pivote para la sumatoria de momentos el punto de corte de la viga, se realiza la sumatoria de momentos:

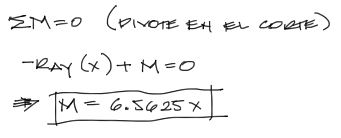
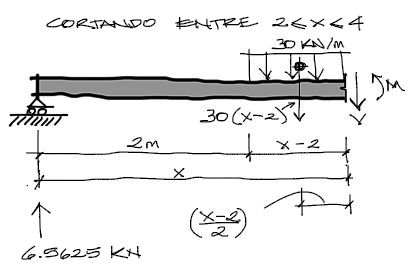
Se repite este proceso haciendo otro corte imaginario en el sector entre la carga y el apoyo B. (El corte se debe realizar en cada tramo donde exista un cambio de carga). Nuevamente estabilizamos primero las fuerzas verticales.

Debes tomar en cuenta además, que para poder encontrar el cortante V y M en función de la coordenada “x”, se debe mantener la distancia del corte imaginario como variable “x”.

Entonces,

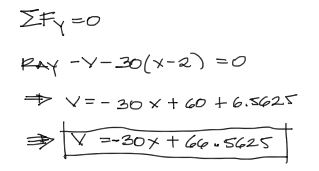
Y de la misma manera que en el anterior tramo, tomando como pivote de la sumatoria de momentos en el punto del corte imaginario, tenemos:

Finalmente, realizando el último corte en el último tramo pasando el apoyo B, se repite el mismo procedimiento de los anteriores dos cortes:

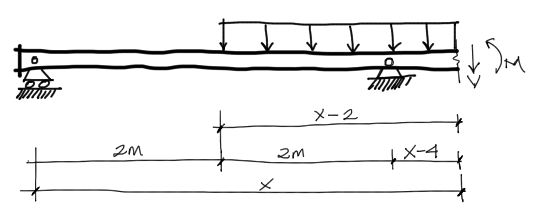
Y realizando la sumatoria de fuerzas verticales y momentos respecto al corte imaginario:

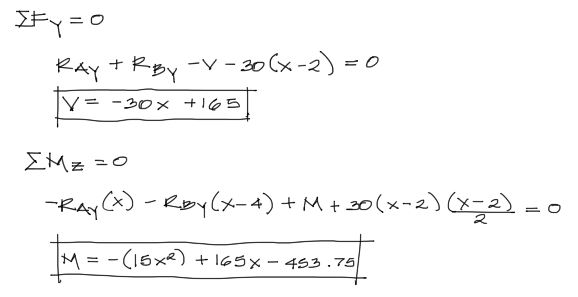
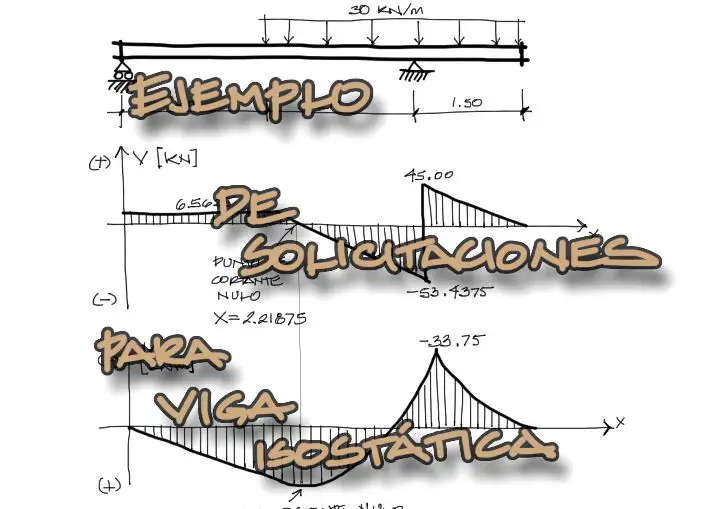
Graficación

Una vez terminado el análisis de las ecuaciones de cortante y de momento flector, solo queda graficarlas de la siguiente manera. Las ecuaciones encontradas de cada tramo corresponden al dominio en x de sólamente ese tramo.

• Por tanto, las primeras ecuaciones se grafican solamente para x desde 0 hasta 2
• Las segundas ecuaciones se grafícan desde x = 2 hasta x = 4
• Las últimas ecuaciones se grafican desde x = 4 hasta x = 5.5

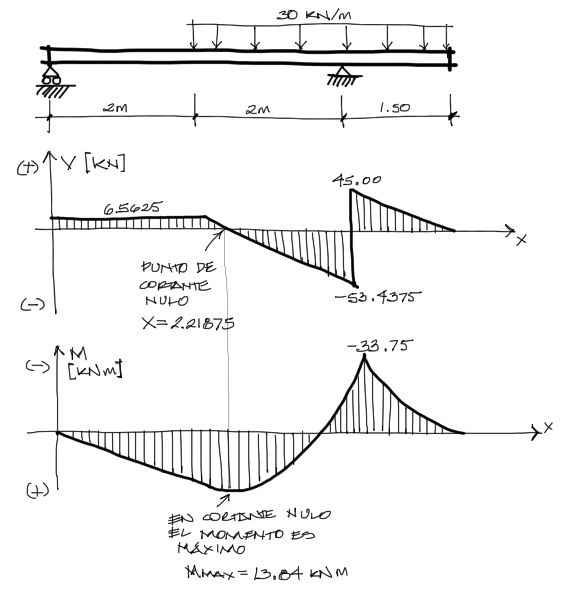
Con esto concluye en análisis

Encontraste lo que buscabas? Hazmelo saber en la caja de comentarios. Saludos

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL←←←