
Reacciones
El equilibrio externo de una viga isostática es uno de los primeros pasos en la resolución de problemas básicos de estructuras.
Para lograrlo, cuando se trate de estructuras en 2 dimensiones, debes siempre utilizar las 3 ecuaciones de equilibrio:
- ΣFx = 0
- ΣFy = 0
- ΣM = 0
Generalmente en vigas la resolución de ΣFx = 0 será inmediata.
La solución de ΣFy = 0 y ΣM = 0 consistirá en un sistema de dos ecuaciones con dos incógnitas. Sin embargo si se escoge bien el punto de pivote de la ΣM=0, una de las incógnitas desaparecerá de esta última y las incógnitas podrán resolverse por simple despeje.
Enunciado
Resolver las reacciones de la siguiente viga:
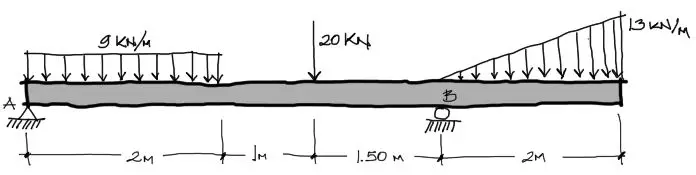
Solución
El ejercicio puedes verlo resuelto en el vídeo siguiente, o seguir un análisis más detenidamente en el texto que te presento más abajo.
Para resolver la viga, debes primeramente convertir las cargas distribuidas en una carga puntual equivalente concentrada en su centroide:
Además puedes comenzar a dibujar las reacciones como vectores en los apoyos. Nota como aparece una reacción en X en el apoyo fijo, pero no así en el apoyo móvil
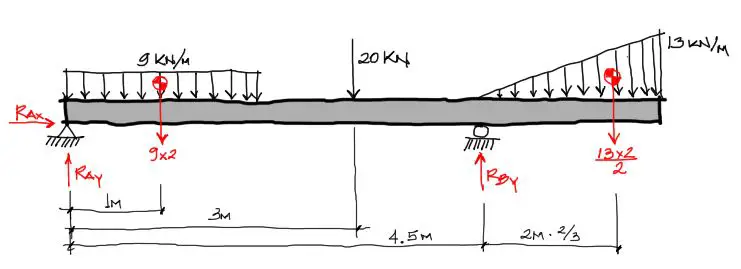
Luego, se puede comenzar a aplicar las 3 ecuaciones mencionadas arriba.
Comenzando por la ΣFx = 0:
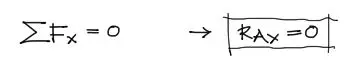
Luego se realiza la ΣFY = 0. En este caso se incluyen en la ecuación todas las fuerzas verticales:
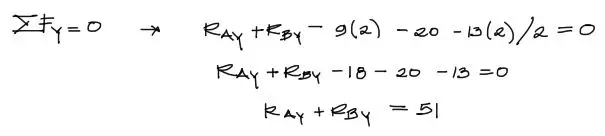
Esta ecuación aun no puede resolverse pues tiene dos incógnitas.
Para resolver una de las dos reacciones, hacemos pivote en A para la ΣM = 0. De esta manera se anulan en la ecuación tanto Rax como Ray pues ambas pasan por el punto de pivote:
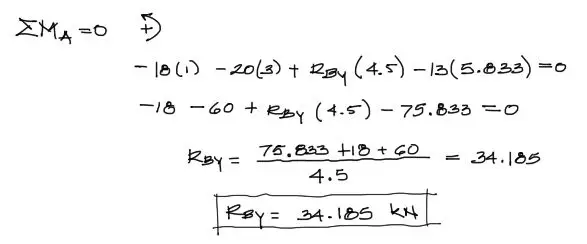
Notarás las siguientes aclaraciones:
- Los momentos de fuerza generados por los vectores fuerza son positivos cuando intentan girar en el sentido antihorario respecto a A
- Los brazos de los momentos de fuerza se miden todos respecto al punto A
- El brazo de la resultante de fuerza de la carga triangular es el resultado de sumar (4.5+2·2/3)[m]
Con todo aclarado, se obtiene la reacción Rby que puede reemplazarse en la ecuación de ΣFy = 0:

Con lo cual se tienen todas las reacciones encontradas.
Dibujando los resultados:
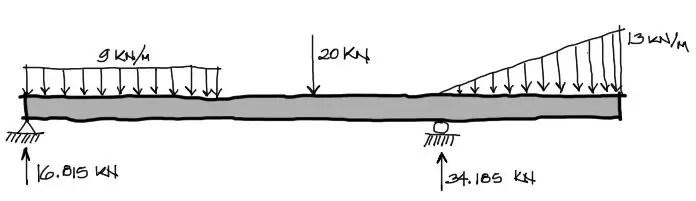
autor: Marcelo Pardo
→ → → A CONTINUACIÓN, SOLICITACIONES DE ESTA VIGA ISOSTÁTICA → → →
← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←


Gracias ingeniero, me gustaría saber como se pueden determinar las reacciones en el extremo de un empotramiento, cuando se tiene una sección no prismática en la cual varía la altura de la sección transversal. A la viga se le aplica una carga uniformemente distribuida. Gracias
Ana buenas tardes. Si pudieras mandarme el enunciado por telegram, podría ayudarte. numero: +591 698 12366
Muchas Gracias Ingenieroo ggg
Muchas Gracias Ingenieroo
MUCHAS GRACIAS INGENIERO, MUY VALIOSA SU PRESENTACION Y EXPLICACION.
Muchas gracias Jose!
Todo muy bien explicado, me sirvio mucho, gracias por su tiempo.
Muchas gracias Alejandro!
soy Mario Flores Fernandez, puedo comunicarme con Ud. para realizar consultas. mi celular es 999503300, en wassap 999503300