Enunciado
Se pide resolver la siguiente viga hiperestática por el método de la elástica de la viga:
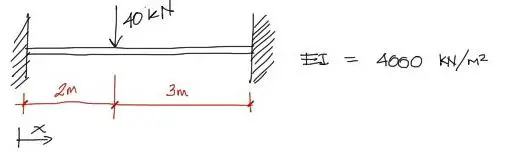
Resolución
División de tramos
Primero, analizando el problema se ve que la viga contiene una carga puntual que genera una discontinuidad en los diagramas de momento flector y cortante de la viga. Si estimamos los diagramas de M y V cualitativamente para la viga, se tiene:
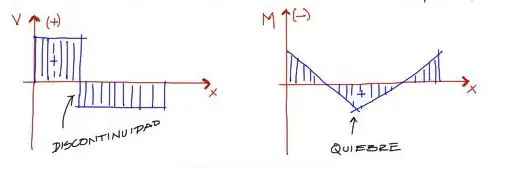
Por tanto, se necesitará dividir la viga en dos tramos. Un primer tramo de 0 a 2, y otro segundo tramo de 2 a 5.
Integración de las ecuaciones diferenciales de la elástica
Luego, las cargas distribuidas para cada uno de estos dos tramos es cero. Entonces q1 = 0 y q2 = 0. Reemplazando en la ecuación de la elástica y comenzando a integrar en ambos tramos se tiene:
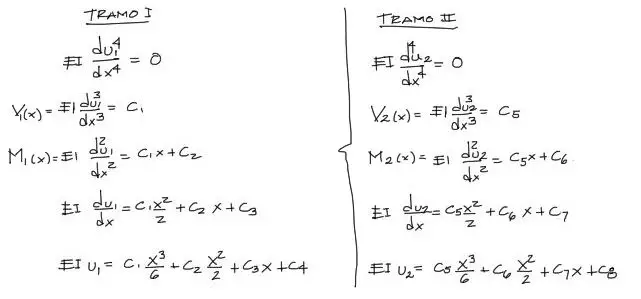
Se puede observar que se generan 8 constantes de integración, C1, C2, … C8, que deben resolverse para así tener las ecuaciones de cortante, momento flector, pendiente y deflexión de la viga.
Para las 8 constantes de integración (incógnitas del problema) se deben entonces encontrar 8 condiciones de borde que satisfagan este problema en particular.
Condiciones de contorno
Cuatro de estas ocho condiciones salen de los empotramientos de los extremos de la viga, donde sabemos que la deflexión u = 0 y su pendiente du/dx = 0, debido a que la viga en estos dos extremos no se desplaza hacia abajo, ni gira. Por tanto las primeras 4 condiciones de contorno son:

El truco para encontrar las otras cuatro condiciones de contorno consiste en enfocarse en la conexión que existe entre los dos tramos mediante el siguiente análisis:
Para la relación de cortantes entre el primer y segundo tramo, se debe razonar pensando que el cortante V2 es igual al cortante V1 al que se le resta el valor de la carga, de -40KN. Así, se tiene:
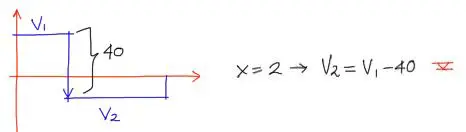
Las otras tres condiciones son más sencillas. De los diagramas cualitativos al comienzo del artículo puedes apreciar que el momento flector interesecta y se encuentra en x=2, por tanto M1 = M2.
Ademas, las pendientes de ambos tramos así como las deflexiones deben ser iguales en x=2, debido a la continuidad de la viga. Por tanto se tiene para las últimas tres condiciones de contorno:

Sistema de ecuaciones
Se van reemplazando los valores de las condiciones de contorno en cada una de las ecuaciones de la elástica arriba. Por ejemplo, la condición 1) x=0 -> u1 = 0 se debe reemplazar en el lugar donde se tenga u1 en su forma no derivada, y en esta misma ecuación se reemplaza x = 0. En este caso haciendo el respectivo reeemplazo, se obtiene C4 = 0.
Se realiza paulatinamente el reemplazo de cada una de las condiciones de contorno en los puntos X respectivos, y se tiene el siguiente sistema de 8 ecuaciones con 8 incógnitas:
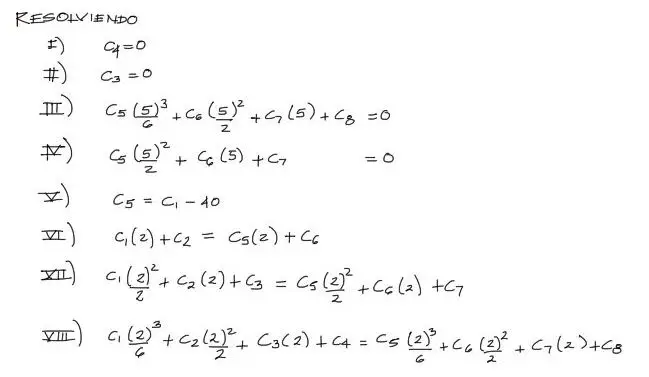
Este mismo sistema de ecuaciones puede resolverse matricialmente de forma sencilla. Para eso creamos el arreglo Ax = B de donde para obtener las incógnitas (Constantes de integración) se tiene x = inv(A)*B.
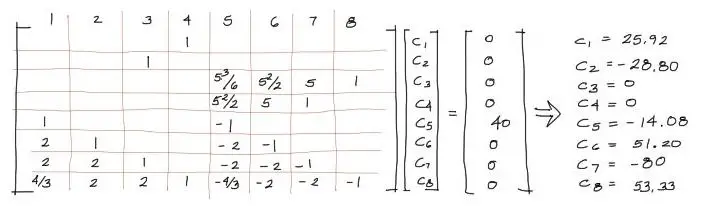
Graficación de los diagramas.
Las ecuaciones resueltas se obtienen reemplazando las constantes C1 a C8 dentro de las ecuaciones de la elástica en sus respectivas posiciones.
En esta publicación solamente se reemplazarán las constantes en la ecuación de momento de ambos tramos y en las ecuaciones de deflexión, y se dejará al lector como ejercicio el reemplazo y graficación del cortante V y pendiente de deflexión.
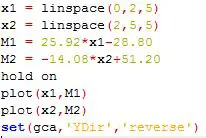
Los momentos flectores de ambos tramos y sus gráficas entonces son:
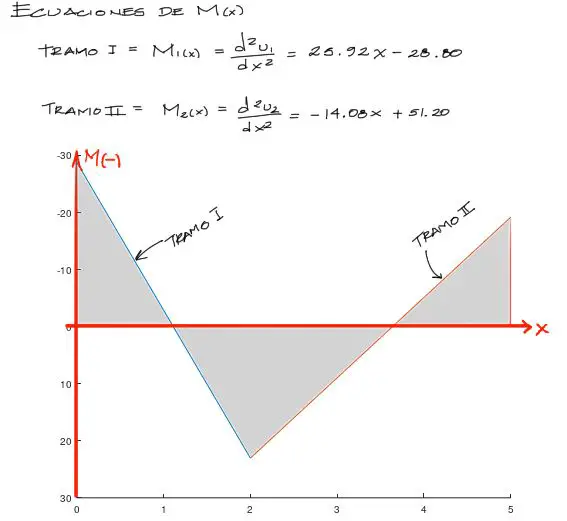
Si te interesa la graficación por Matlab, el script para graficar los momentos es el siguiente:
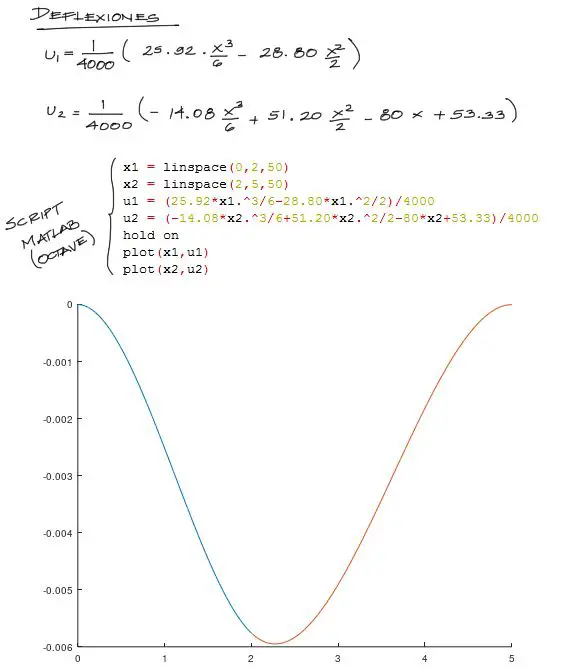
Para las deflexiones se procede de manera similar. A continuación muestro las ecuaciones, código en Octave (la versión gratuita de matlab) y la gráfica de deflexión
Con esto termina el ejercicio. Espero te haya sido útil.
autor: Marcelo Pardo
← ← ← VOLVER A TABLA DE CONTENIDO DE ANÁLISIS ESTRUCTURAL← ← ←