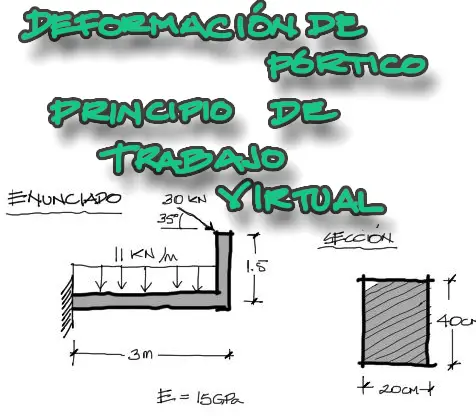
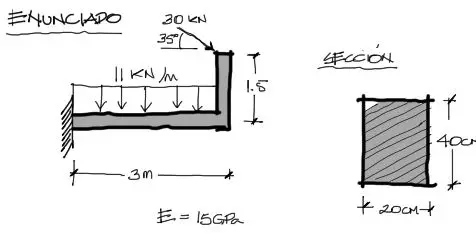
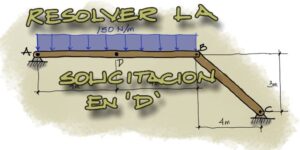
Enunciado
Se pide resolver el desplazamiento horizontal en el extremo superior derecho del pórtico mostrado. Se debe emplear el método de principio de trabajo virtual.
Solución
Primeramente se debe convertir el módulo elástico en las mismas unidades de la carga. Para la deformación axial de la pieza se necesita el área de la sección transversal. Por otro lado para la deflexión calculamos la inercia de la figura respecto al eje horizontal transversal a la sección de la pieza.
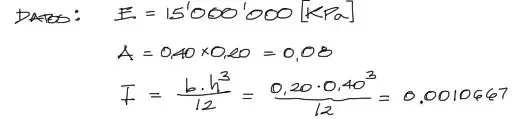
Las fórmulas a aplicar para la resolución del problema son las siguientes:
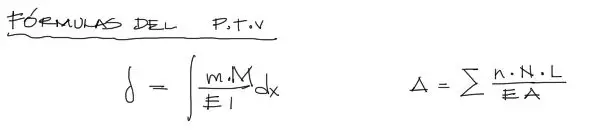
Donde:
– “m” es el momento flector en el pórtico producto de una carga virtual en el punto donde se desea calcular el desplazamiento y apuntando en la dirección de este desplazamiento.
– “M” es el momento flector producto de las cargas reales
– “n” es la solicitación normal a la pieza producto de la misma carga unitaria
– “N” es la solicitación normal producto de las cargas reales
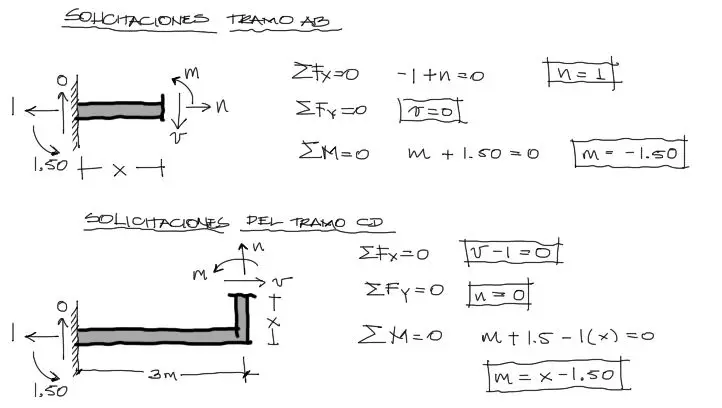
Equilibrio externo y solicitaciones producto de cargas reales
Producto de las cargas reales, se realiza el equilibrio externo del pórtico aplicando las 3 ecuaciones de equilibrio:
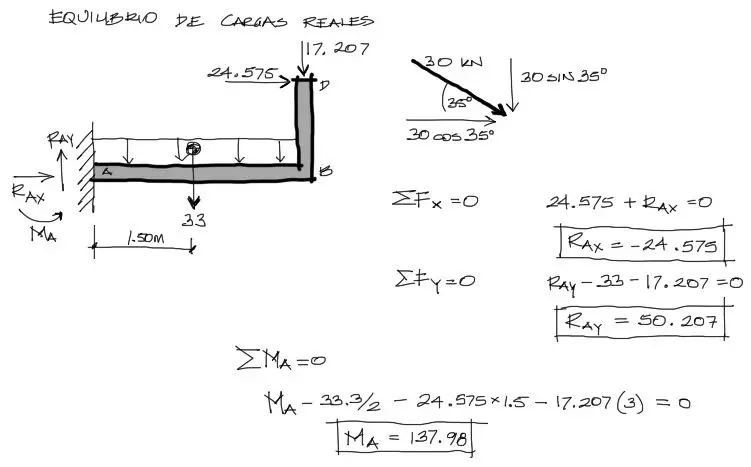
Nota que se aplica la convención de signos de giro (rotación de momento) antihorario positivo.
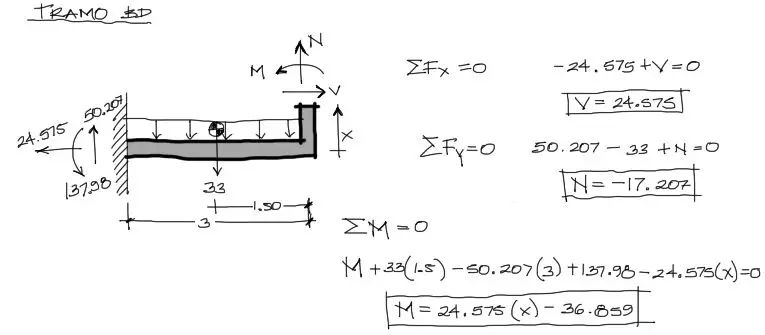
Luego se hacen cortes imaginarios en los dos tramos del pórtico. Cada uno de estos tramos está gobernado por una ecuación de M y N
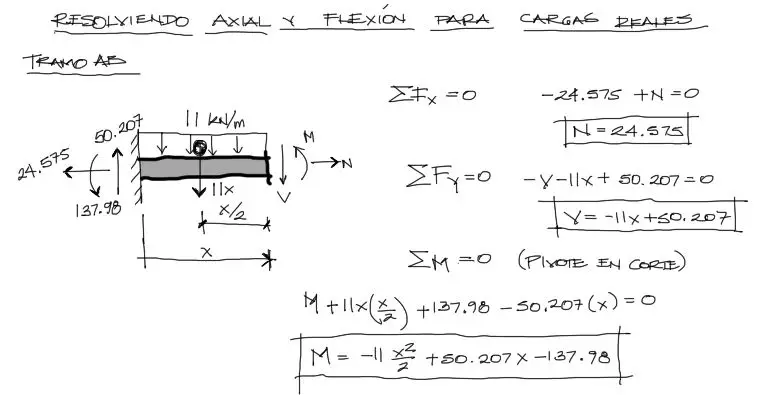
Para el tramo BD se asumen coordenadas X que acompañen el eje longitudinal del tramo. Esto es muy común en pórticos.
Equilibrio externo y solicitaciones producto de carga horizontal unitaria (virtual)
Se carga el pórtico nuevamente con la carga unitaria en la dirección en la cual se busca conocer el desplazamiento en el punto D. Luego se realiza el equilibrio externo encontrando sus reacciones:
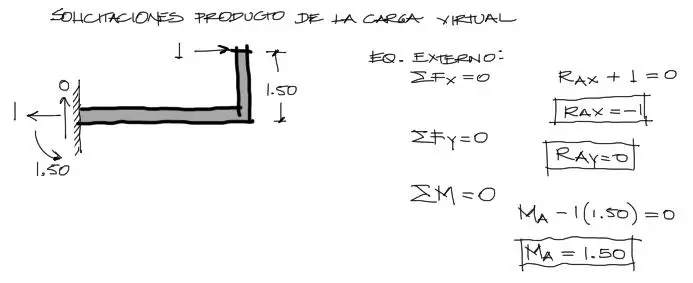
Luego se calculan las solicitaciones internas en forma de ecuación cortando los tramos del pórtico a una distancia X local para cada tramo. El X local debe coincidir con las coordenadas locales consideradas para las cargas reales:
Ecuaciones de Principio de Trabajo Virtual
Las ecuaciones combinadas del Principio de Trabajo Virtual tanto para las deformaciones por flexión como para las deformaciónes por carga axial son:

Nota que el último término correponde a la deformación por cargas axiales. La sumatoria corresponde a la suma de las cargas axiales de todos los tramos. Aplicando los valores a las ecuaciones:
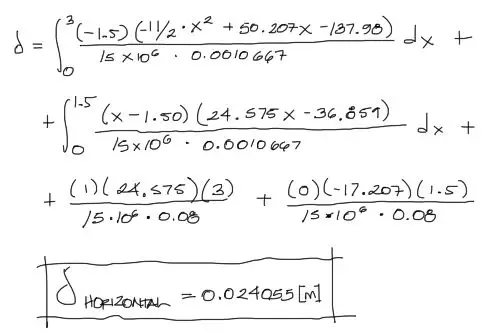
Recalco siempre que deben introducirse los datos en unidades consistentes. Si la carga está en KN/m, los módulos elásticos , inercias y áreas deben estar correspondientemente en KN y m.
autor: Marcelo Pardo
Extraordinario Gracias