Planteamiento

El elemento que se analizará, es el más sencillo de los elementos para análisis matricial.

Si se tiene una barra recta de una longitud L, y de sección transversal A, como la mostrada, esta barra puede idealizarse como un elemento lineal con dos nudos en los extremos. Estos nudos servirán de conexión con otros elementos en caso de que así se requiera.

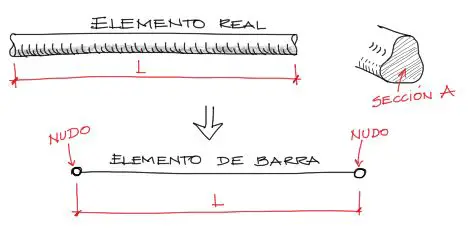
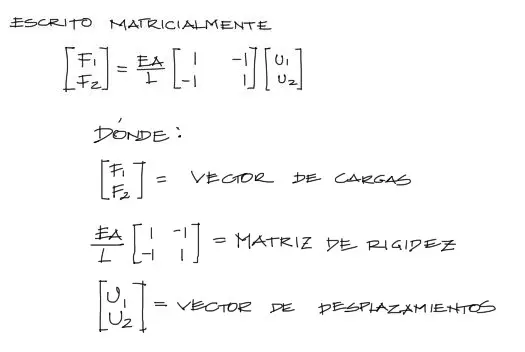
Relación entre desplazamientos de los nudos y fuerzas externas

El trabajo consiste en encontrar una relación entre los desplazamientos de la barra y las fuerzas externas, mediante las solicitaciones internas de esfuerzo y deformación.

Imaginaremos entonces que los nudos se desplazan unas distancias u1 y u2:

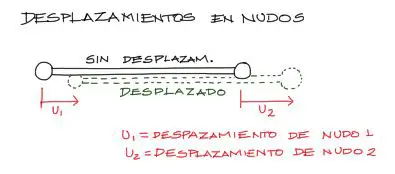
Además de estos desplazamientos, existen fuerzas externas que se aplican en la barra, que por equilibrio serán iguales y opuestas:

Ahora bien, podemos plantear una relación entre los esfuerzos internos de la barra y las deformaciones unitarias que estos esfuerzos generan:

En estas ecuaciones, se puede poder todo en función de las fuerzas y de los desplazamientos conociendo la definición de esfuerzo y de deformación unitaria. Nos centraremos en este caso en el nudo 2, donde la deformación unitaria es ξ = (u2-u1)/L.

Luego se forma una ecuación donde F2 está intrínsicamente relacionada con los desplazamientos en los extremos.

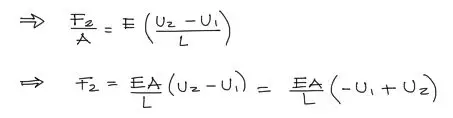
Debido a que F2 = -F1, entonces se puede escribir la ecuación anterior en función de F1:

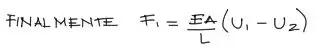
Se forma entonces un sistema de ecuaciones en función a 4 variables. F1, F2, u1, u2

Escrito el sistema matricialmente, se tiene lo siguiente:

Ejemplo muy sencillo

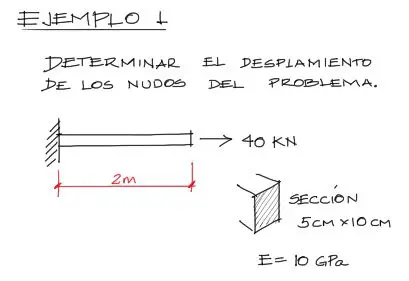
Enunciado

La mejor manera de entender la teoría detrás de estas matrices es mediante un ejemplo. Se abordará en este caso el ejemplo más sencillo de todos, donde se analizará una sola barra sometida a una carga axial, con valores numéricos como los mostrados.

Solución

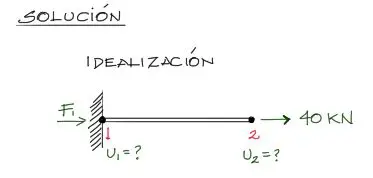
Se idealiza la estructura enumerando los nudos y mostrando las fuerzas y deformaciones que actuan:

Por otro lado los datos del problema deben ser calculados en unidades consistentes para el problema, transformando en este caso todo a unidades de KN, m.

Luego reemplazamos los datos en el sistema de ecuaciones en forma matricial:

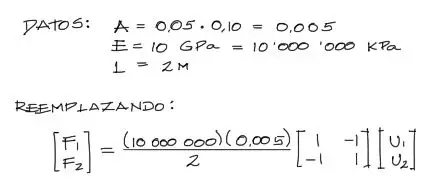
Condiciones de contorno

El problema no está completo sin antes estableces las condiciones de contorno del problema. Notarás que en el apoyo el nudo está restringido al movimiento, por tanto el desplazamiento u1 será igual a cero. Además, justo donde el desplzamiento es cero, aparece una reacción R1 que se genera por la restricción. En el otro extremo el nudo es libre de moverse y por tanto u2 es desconocido. Sin embargo la fuerza sí es conocida, y es igual a la carga de 40 KN:

reemplazando estos datos en el sistema:

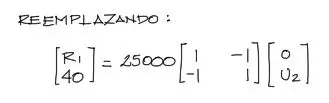
Este sistema, como todos los que se resolverán más adelante en otros ejemplos, no es típico, pues tiene incógnitas a ambos lados de la igualdad. Para resolver este problema se puede aislar el sistema en un sistema más pequeño donde solamente se tengan incógnitas para los desplazamientos.

Para lograr esto, multiplicaremos el desplazamiento conocido u1 = 0 por la matriz de coeficientes (la matriz de rigidez). Haciendo esto, en este caso en particular, se obtiene una ecuación suelta donde R1 ya no forma parte de las incógnitas, y u2 puede despejarse fácilmente:

Conocido u2, se puede reemplazar este dato en el sistema original y obtener R1. La segunda fila del sistema nos devuelve una identidad, que simplemente indica que el sistema de ecuaciones fue bien resuelto.

Si bien este es un ejemplo sumamente sencillo, ayuda a entender el propósito del método. A partir de estas soluciones incluso se puede llegar a averiguar el esfuerzo interno en el elemento. Sin embargo se dejará este ejercicio para ejemplos más interesantes que este.

← ← ← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS← ← ←

autor: Marcelo Pardo