Planteamiento del elemento

Se ha visto en anteriores publicaciones la relación entre desplazamientos y fuerzas en los nudos para un elemento de barra sometido solo a fuerzas axiales. Esta documentación la encuentras en los enlaces:
– Matriz de rigidez de elemento de barra en 1D
– Matriz de rigidez de elemento de cercha en 2D

Se quiere conocer ahora la relación entre los desplazamientos de los nudos y las fuerzas en estos nudos, pero en un entorno tridimensional como el mostrado en la figura:

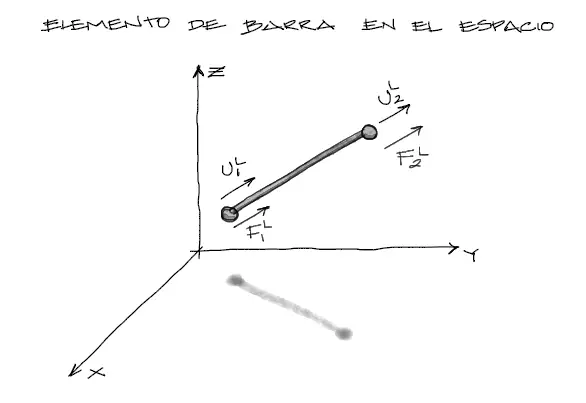
Recordando de la teoría anterior, la relación entre desplazamientos y fuerzas externas para elementos en 1 dimensión es:

Descomposición del vector de desplazamientos

Nos concentramos momentaneamente solo en el nudo 1 del elemento de la gráfica anterior. El desplazamiento U1L del nudo 1 está dirigido en la dirección del eje longitudinal de la barra en análisis.

Este desplazamiento vectorial U1L podemos descomponerlo en sus componentes cartesianas en coordenadas globales U1, U2, U3, a partir de la definición de cosenos directores como sigue:

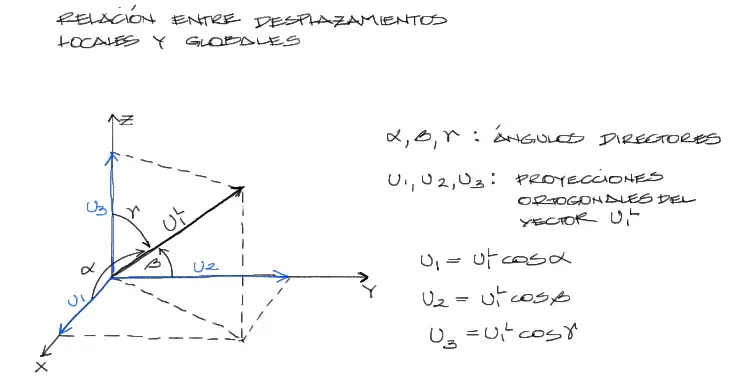
A la vez sabemos que para los cosenos directores de un vector, los ángulos α, β, ɤ se relacionan entre si a partir del cuadrado de sus cosenos y se iguala a uno como en la siguiente ecuación:

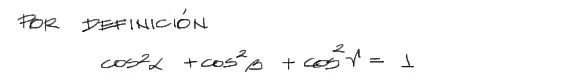
Si los cuadrados de los cosenos los reescribimos descomponiendo el exponente, se tiene

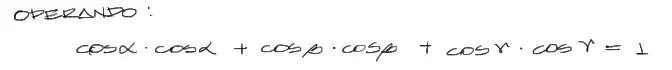
Pero a la vez, de la definición de proyección de un vector mencionada arriba, podemos despejar los cosenos directores y se tiene:

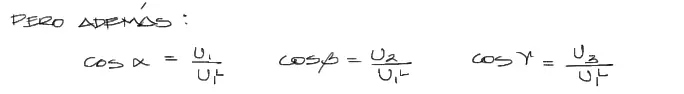
Ahora reemplazamos uno de los cosenos de la penúltima ecuación con los cosenos despejados de la última figura mostrada.

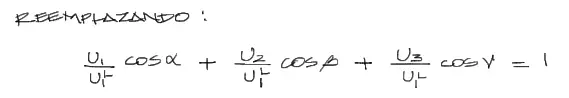
Notemos que UlL es factor común de los tres términos de la expresión izquierda que puede factorizarse y pasar a multiplicar al miembro derecho:

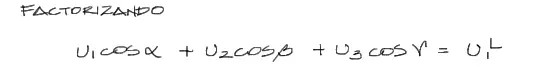
El mismo procedimiento puede lograrse para el desplazamiento U2L del nudo del otro extremo de la barra, en el entendido de que sus desplazamientos globales son U4, U5, U6:

finalmente podemos escribir en forma matricial el sistema de dos ecuaciones de la siguiente manera:

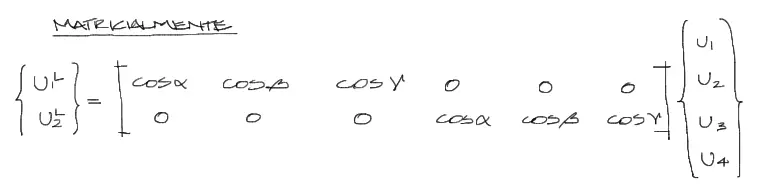
Es conveniente abreviar estas matrices para las operaciones posteriores. La matriz de cosenos directores suele denominarse matriz de transformación de KL (KL es la matriz de rigidez del elemento en 1D) y la denominaremos como B:

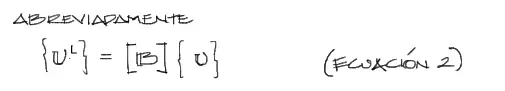
Reemplazo en la ecuación principal

Tenemos la relacion entre desplazamientos y fuerzas en 1-D o en coordenadas locales (ecuación 1) y la ecuación 2 recientemente encontrada. Podemos entonces reemplazar los desplazamientos UL de la ecuación 2 dentro de la ecuación 1, obteniendo:

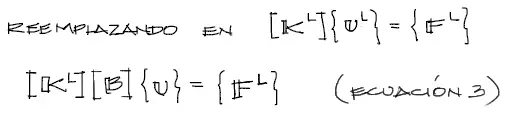
Temporalmente dejaremos aquí la última ecuación encontrada.

Descomposición del vector de Fuerzas

Al igual que con el vector de desplazamientos locales, la fuerza local F1 local puede descomponerse en sus 3 componentes cartesianas F1 F2 F3:

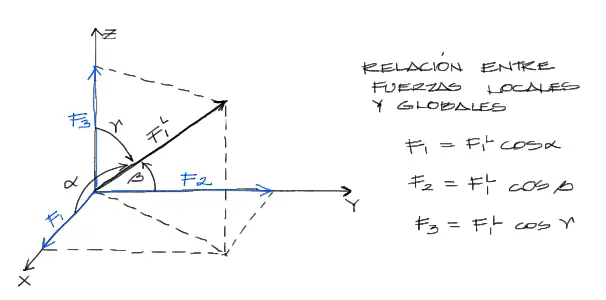
y análogamente para el otro nudo tenemos relaciones similares:

Las fuerzas globales F1, F2 ….F6 pueden reescribirse matricialmente con las fuerzas locales F1L y F2L a partir de la siguiente relación:

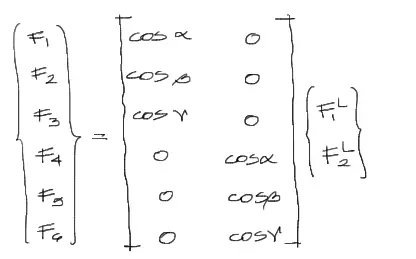
y Abreviadamente podemos expresar lo anterior, de la siguiente manera:

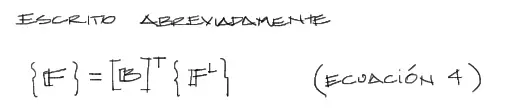
Reemplazo en la ecuación principal de rigidez

La ecuación 3 podemos reemplazarla dentro de la última ecuación 4 encontrada como sigue:

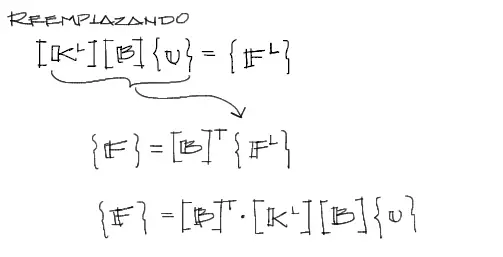
Esta última ecuación obtenida relaciona las fuerzas en coordenadas globales con los desplazamientos en coordenadas globales para un elemento de barra deformado axialmente en un espacio en 3 dimensiones.

matriz de rigidez de elemento de cercha en 3 Dimensiones

autor: Marcelo Pardo

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←