Enunciado
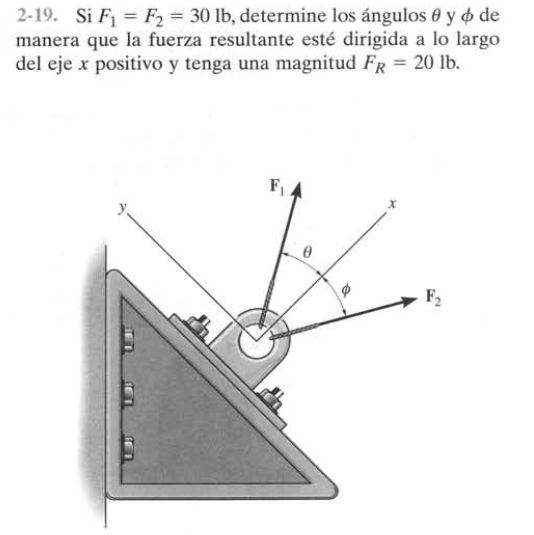
Se pide encontrar los ángulos que generarán una resultante que caiga enteramente sobre el eje X
Solución
Paso 1 – descomposición de vectores
Este ejercicio entrena al lector a entender que los ejes cartesianos no siempre deben estar alineados con la horizontal.
Primero debemos encontrar las componentes de los vectores descompuestos, así como las componentes de la resultante. En este ejercicio en particular las magnitudes son datos y los ángulos incógnitas. por tanto descomponemos los vectores F1 y F2 en función a estos ángulos incógnita.
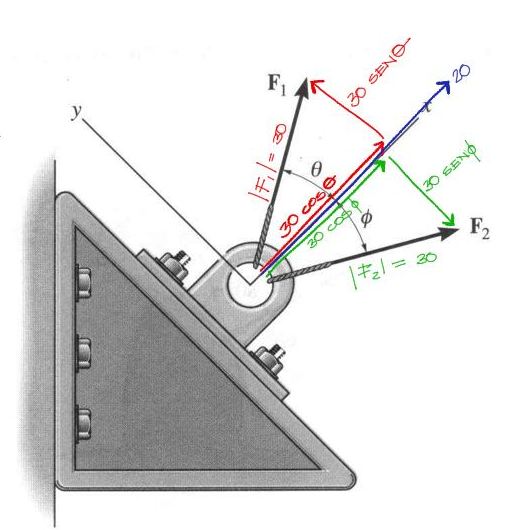
A la vez, debido a lo que indica el enunciado, la resultante debe tener magnitud de 20 y que tenga solamente componente “X” igual a 20, y componente Y = 0
Paso 2 – Suma de componentes
Como en todo ejercicio de vectores, la suma de dos vectores es la suma de sus componentes. En este caso se suma F1+F2 = Fr. Para esto sumamos sus componentes en X y componentes en Y, y conformamos un sistema de dos ecuaciones con dos incógnitas.
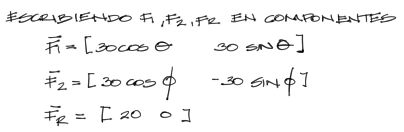
Paso 3 – Resolución del sistema de ecuaciones
Al sumar componentes en X en una ecuación y componentes en Y en otra ecuación se conforma el siguiente sistema:

Se resuelve el sistema de ecuaciones primero resolviendo la ecuación 2.
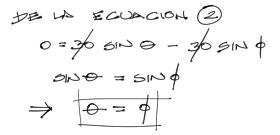
Reemplazando cualquiera de los ángulos (pues son iguales) en la ecuación 1, se resuelve finalmente que los ángulos ɸ y θ son:
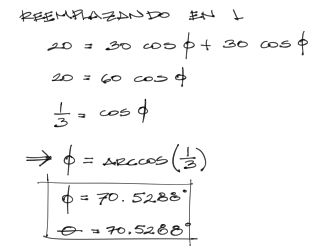
El ángulo de F1 y F2 respecto a X son entonces ambos, 70.52°.
Vídeo
Si prefieres ver el vídeo de resolución, está a continuación.
autor: Marcelo Pardo