Concepto de momento de fuerza
El momento de una fuerza respecto a un punto consiste en un torque producido por una fuerza aplicada perpendicular a la distancia entre el punto y la línea de acción de la fuerza.
Si bien este concepto es un poco simplista, nos aproxima al concepto más completo.
Concepto escalar
El concepto escalar de un momento de fuerza es precisamente el mencionado en el anterior subtítulo.
Se puede imaginar al momento de una fuerza como una palanca hecha por la fuerza, respecto al punto al cual quiere aplicarse el momento de fuerza.

No importa donde se encuentre la fuerza, siempre puede dibujarse la línea de acción de esta fuerza y una línea perpendicular desde el punto hasta la línea de acción. Así se obtiene la distancia o brazo de palanca de la fuerza.
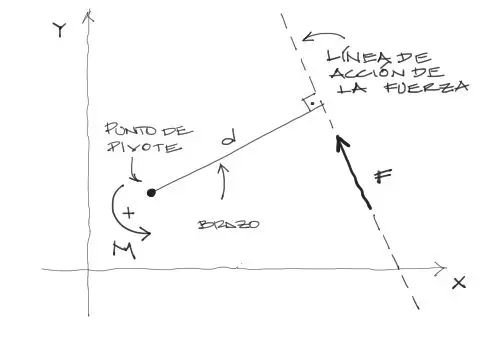
Posteriormente, el momento de una fuerza se define como M = d·F
Convencionalmente el signo del momento de fuerza será positivo si el giro producido por la fuerza al rededor del punto de pivote es antihorario, y será negativo si el giro es horario. Sin embargo existe bibliografía donde ocurre exactamente lo contrario, sin que esta convención última esté incorrecta. Lo que se debe tomar siempre en cuenta es que cualquiera sea la convención que se adopte, debe mantenerse hasta el final de los cálculos.
Para un ejemplo de este concepto, puedes ver el siguiente vídeo
Concepto vectorial
El concepto vectorial del momento de una fuerza es un poco más complejo, sin embargo analíticamente es mucho más fácil de calcular que en el concepto escalar.
Imagina que se tiene el punto de aplicación del momento y el vector fuerza “F”. Además existe un vector posición “r” que indica el punto de aplicación de la fuerza. Este vector “r” no necesita ser perpendicular a la fuerza “F” y está es una gran ventaja.
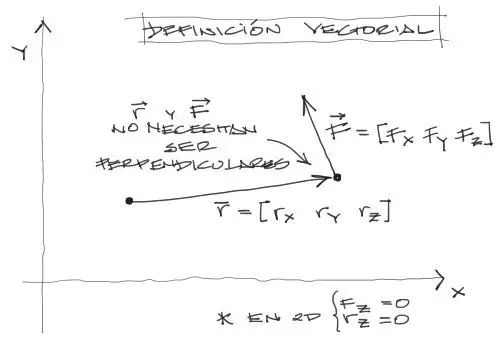
Notarás que el resultado de M = r x F es también un vector. Para obtener el resultado escalar lo que se debe hacer es obtener el Módulo |M| del vector M.
La multiplicación vectorial no es conmutativa
Se debe notar que al multiplicar rxF obtenemos un resultado diferente que si multiplicamos Fxr. Por tanto debemos siempre respetar el orden de la multiplicación al aplicar dicha fórmula.
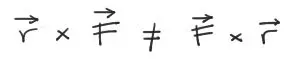
Siempre en 3 dimensiones
Algo que debemos tomar en cuenta al trabajar con la fórmula vectorial del concepto de momento de fuerza, es que los vectores deben estar formulados en 3 dimensiones por más de que el problema sea en 2 dimensiones.
Asumamos por ejemplo que el vector brazo r tiene componentes [rx, ry, rz]. Además el vector F tiene componentes [Fx, Fy, Fz].
La multiplicación vectorial de estos dos vectores será entonces:

El vídeo siguiente muestra un ejemplo del concepto.
Si tienes dudas, puedes escribirlas en los comentarios
autor: Marcelo Pardo