Planteamiento
Cuando resolvemos estructuras hiperestáticas, normalmente encontramos los los momentos en los extremos de un tramo. Luego debemos encontrar los diagramas de momento flector de todo el tramo a partir de los momentos en los extremos.
La ecuación que graficará el diagrama de momentos flectores a lo largo del tramo depende además del tipo de carga aplicada. en este caso nos concentraremos en un tramo con carga distribuida, y momentos M1 y M2 en los extremos.

Notemos que en la mayoría de los métodos de cálculo de vigas hiperestáticas, los momentos obtenidos M1 y M2 obedecen a la convención de signos ANTIHORARIO POSITIVO. Cuando procedemos a encontrar los diagramas de momento flector de la viga, esta convención debe cambiarse a la que indica que LOS MOMENTOS SON POSITIVOS SI TRACCIONAN LAS FIBRAS INFERIORES DE LA VIGA.
Ecuación de la carga
Se procederá a encontrar el diagrama de momentos a partir de la teoría de la elástica de la viga. Por tanto, necesitamos primero conocer la ecuación de la carga distribuida. Como la carga distribuida es una recta, la forma de su ecuación es:

donde no conocemos aun los coeficientes A y B de dicha recta. Sin embargo conocemos los valores de Momento en los extremos de la viga para las coordenadas x1 y x2 respectivamente:
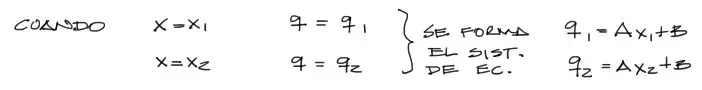
Imponiendo estos valores en la recta dos veces, se forma el sistema de ecuaciones mostrado, donde las incógnitas son A y B. Esto se puede resolver fácilmente despejando la variable B de la segunda ecuación y reemplazandola en la primera. Hecho esto reemplazando el valor de A encontrado en cualquiera de las dos ecuaciones para despejar B. Se obtiene entonces:
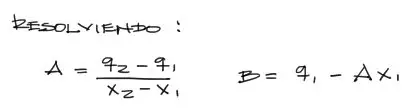
Ecuación de la elástica de la viga
Habiendo encontrado los valores de A y B, podemos ahora aplicar la teoría de la elástica de la viga:

Sabemos que la primera integral de la elástica de la viga es el cortante y la segunda integral es el momento flector.
Al momento de integrar la ecuación de la elástica se generan dos constantes de integración C1 y C2. Estas son incógnitas del problema que debemos averiguar.
Condiciones de contorno
Al igual que al momento de encontrar A y B, conocemos los valores de M(x) en los extremos del tramo, por tanto podemos imponer estas condiciones de contorno en la ecuación de momento flector genérica recién encontrada.
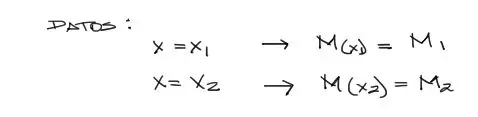
Luego reemplazamos estos valores dentro de la ecuación de momento flector y nos queda un sistema de dos ecuaciones con dos incógnitas.
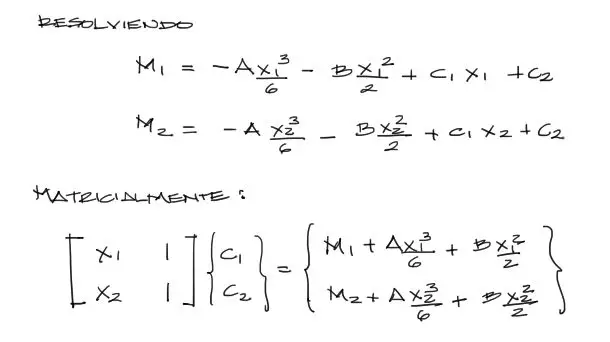
esto se puede resolver numéricamente matricialmente para así obtener los valores de C1 y C2. Con esto se termina el problema y se tiene la ecuación de momento flector lista para graficarse.
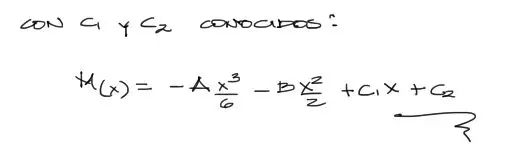
Video Ejemplo
En el vídeo que publiqué hace años muestro este proceso con un ejemplo. Si minutos disponibles de estudio, te invito a verlo:
autor: Marcelo Pardo