Continuación
En la anterior publicación habiamos logrado encontrar la matriz de rigidez de 25 elementos. Si sigues el ejemplo de cerca probablemente incluso hayas podido descargar las 25 matrices de rigidez para la comprobación por tu cuenta.
Rotación de elementos a su posición final
Hasta el momento cada una de las barras calculadas tiene una orientación con el eje longitudinal de la barra (eje x’ local) apuntando en la misma dirección que el eje global X. Ahora debemos realizar 3 rotaciones a cada una de las matrices de rigidez local, para ubicarlas en su posición global. Para entender mejor lo que se hará puedes revisar la publicación de Rotación de elemento de barra para pórtico en 3D.
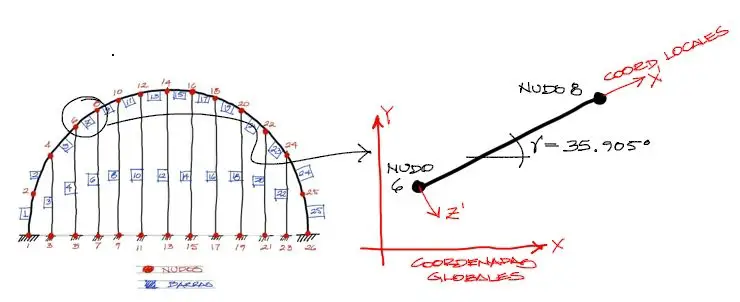
Tomando nuevamente como ejemplo el elemento 7 de nuestro pórtico, debemos rotarlo primero respecto de su propio eje un ángulo α = 90°, luego un ángulo β=0° en altura (ver primera parte de este ejercicio) y finalmente se deberá efectuar el giro de derrape sobre el plano XY del elemento que en este caso para la barra 7 será ɤ=35.905.
La rotación α = 90° para el elemento 7 se vé más o menos así:
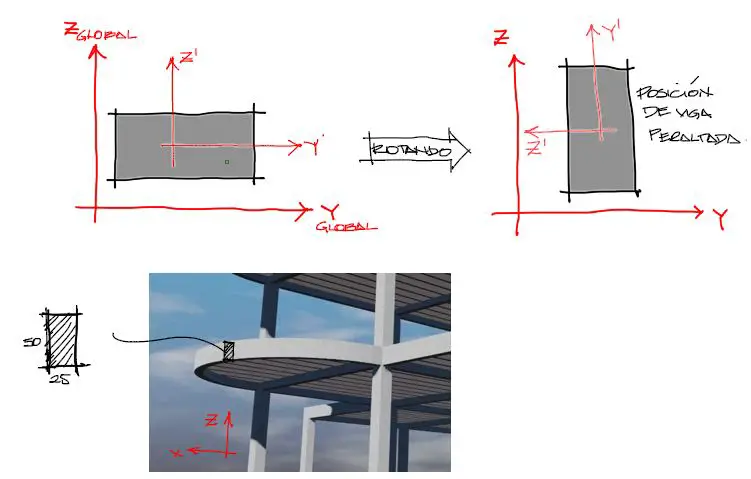La rotación β=0° no se muestra pues la matriz de rigidez luego de esta rotación es idéntica a la matriz rotada respecto a su eje. Luego se aplica al elemento 7 la rotación de derrape girando la barra el ángulo ɤ=35.905° respecto al eje Z global. Gráficamente es como sigue:
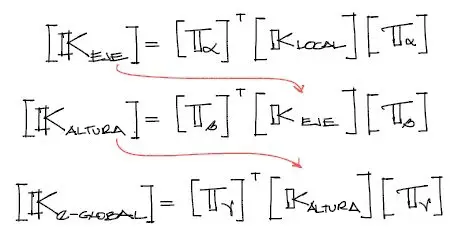
Matemáticamente, la multiplicación de las matrices de rotación por la matriz K_local dan respectivamente los siguientes resultados(ver las fórmulas [Tα], [Tβ], [Tɤ] en la Teoría de rotación de elementos)
De manera abreviada las operaciones son las siguientes:
y de manera en extenso, el resultado de las matrices locales que van siendo rotadas quedan como sigue:
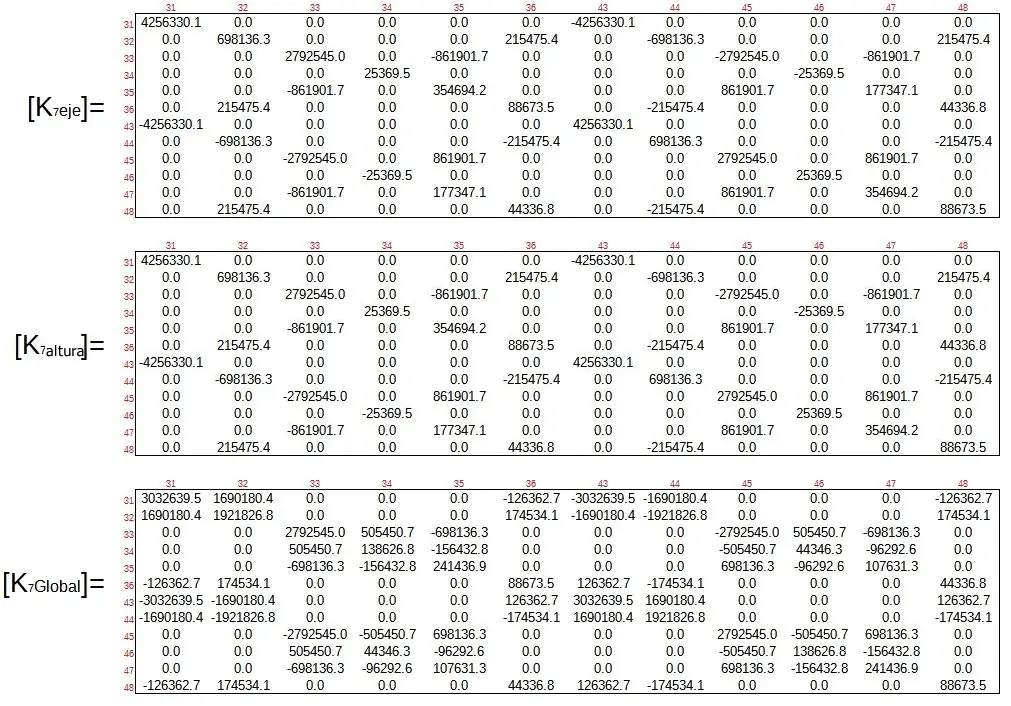Finalmente deben repetirse estas operaciones para todos los elementos del pórtico. Es por eso que este procedimiento debe ser lo más automático posible. Todas las matrices elementales rotadas pueden descargarse en el siguiente zip.
Ensamblaje de la matriz de rigidez global
Debemos tener presente hasta este momento, que tenemos las 25 matrices de rigidez de los elementos ya rotados para ser ensamblados dentro de la matriz de rigidez global de dimensión 156×156. Además hemos citado en la anterior publicación todos los grados de libertad de cada elemento que conforman las posiciones de cada valor de las matrices de cada elemento dentro de la matriz de rigidez global. Volveremos a mostrar esos grados de libertad en la siguiente imagen.
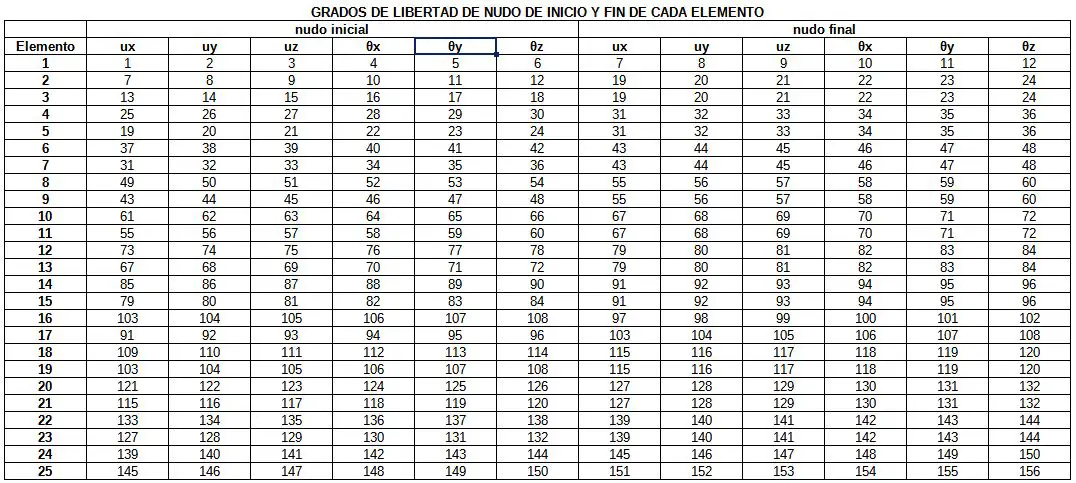Entonces, cada elemento de cada matriz de rigidez debe tomar las posiciones mostradas. Si dos valores de diferentes matrices elementales llegan a la misma casilla, los valores se suman. Finalmente se tiene ensamblada la matriz de rigidez global
Por ejemplo para el caso de la matriz en coordenadas globales del elemento 7, el ensamblaje hacia la matriz global 156×156 será esquemáticamente algo como lo que sigue:
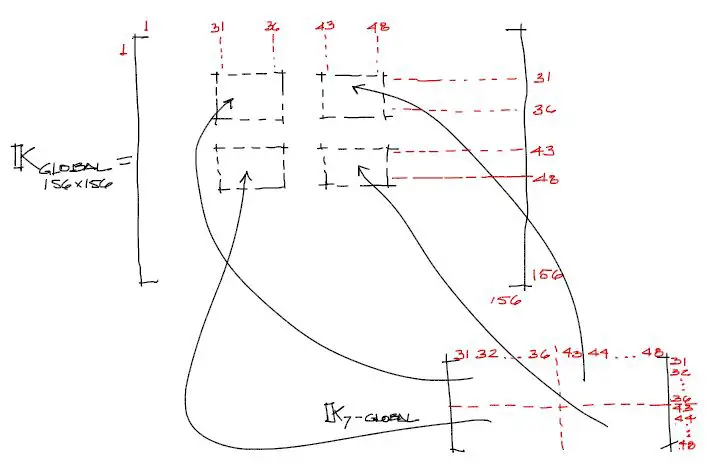Y para el resto de los elementos se procede de igual manera. Finalmente la matriz de rigidez de toda la estructura queda como en la siguiente figura:
Lastimosamente esta matriz es relativamente grande para estándares académicos de pregrado. La matriz para descargar se la puede obtener en el enlace siguiente.
Matriz de rigidez de la estructura
Cargas
Lo que sigue al análisis es la elaboración de la matriz de cargas. Sin embargo dejaremos ese análisis para la siguiente publicación.
autor: Marcelo Pardo
→→→ Voladizo Circular – PARTE 1 →→→ ←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←
Hola ingeniero, una pregunta, en caso de que el eje global Y sea el que representa la altura en los modelos, el ángulo alpha sería cero? Espero su respuesta.
Así es María. No habría que rotar 90° todas las barras
Buenas ingenierio. Los ángulos alpha y bheta siempre se toman como 90° y 0° respectivamente, o solo para este ejemplo en específico
Sebas, es solo para este ejemplo en espefícifo
Y disculpe, hay una forma general para obtener esos ángulos a partir de las coordenadas y la longitud? Basicamente para poder programar
Para bheta sería el mismo procedimiento con el que calculamos ghama no? solo que trabando con las coordenadas en z. Para alpha sería trabajando con las coordenadas en x?