Cálculos previos

En el anterior artículo vimos como se obtiene la matriz de rigidez de la estructura a partir de divisiones formando elementos más o menos del mismo largo. Esa publicación la encuentras HACIENCO CLICK AQUÍ.

Análisis de cargas

Una vez encontrada la matriz de rigidez de la estructura, toca dedicarse al cálculo de las cargas. Para eso, asumiremos los siguientes puntos:

• No se tomará en cuenta el cálculo de peso propio.
• No se suman las cargas de los elementos verticales.
• Se asume que la carga externa de 100 KN/m se transporta con cargas puntuales solamente hacia el arco.

Además haciendo un análisis de las proyecciones horizontales de los tramos de arco, nos damos cuenta de que cada proyección horizontal de cada tramo tiene diferente longitud:

Cada tramo de carga genera q*L/2. de la siguiente manera:

A partir de estas cargas equivalentes en los extremos de cada tramo, podemos cargar el arco con la mitad de la carga de cada tramo, como sigue:

Solo se hizo el ejercicio para los 3 primeros tramos, pero el resto de tramos siguen el mismo patrón.

Vector de cargas puntuales equivalentes

Las cargas acomodadas en los nudos en la imagen anterior, conforman un vector de fuerzas de 33 grados de libertad. Las cargas deben estar acomodadas en los grados de libertad verticales de los nudos dentro del vector de cargas. Los demás grados de libertad horizontales y de giro no reciben carga alguna, por lo que sus valores son cero en el vector {f}.

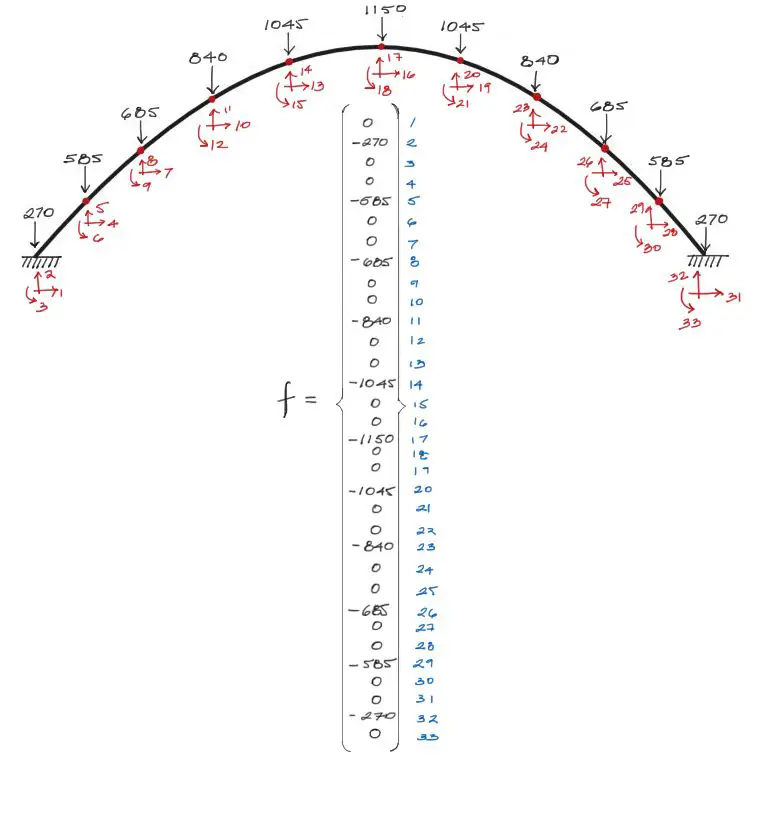
Sistema de ecuaciones completo

El vector de cargas {f} anterior forma parte de un sistema de 33 ecuaciones con 33 incógnitas, como en la siguiente imagen:

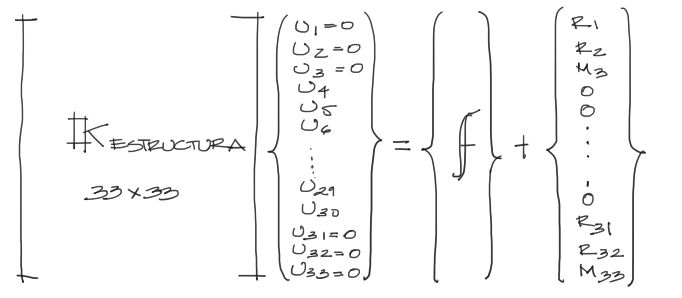
Por comodidad solamente se escriben las matrices simbólicamente tanto para la de rigidez como para la de cargas. El vector de reacciones tiene incógnitas solo en los grados de libertad restringidos. Los grados de libertad libres del vector de reacciones son todos cero.

En los grados de libertad restringidos (1, 2, 3, 31, 32, 33) los desplazamientos toman valor cero, por la naturaleza del apoyo empotrado. Justo en estos grados de libertad, las reacciones son deconocidas.

Para resolver este sistema de ecuaciones es conveniente reordenar los grados de libertad del sistema. Primero se escribirán los grados de libertad cuyos desplazamientos son desconocidos, y posteriormente los conocidos, de la siguiente manera:

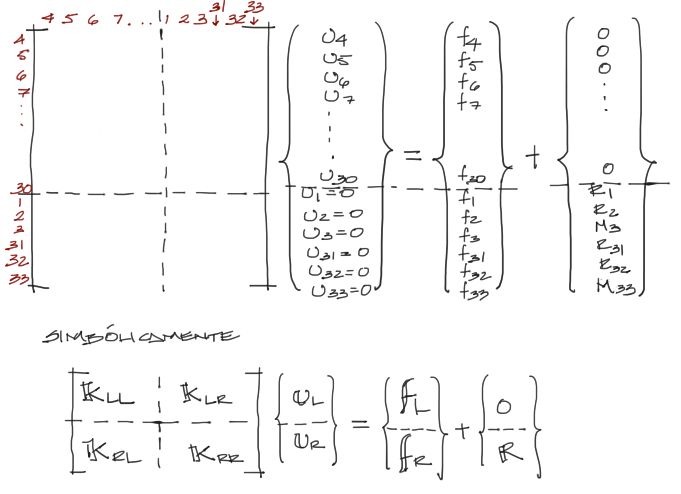
En el sistema anterior, “L” simboliza los grados de libertad libres y “R” los restringidos.

Resolución del sistema de ecuaciones

Reordenado el sistema de esta manera, se puede resolver el sistema de ecuaciones muy fácilmente para los desplazamientos desconocidos:

Y una vez que se cuenta con los desplazamientos libres ya encontrados, se pueden resolver las reacciones a partir de:

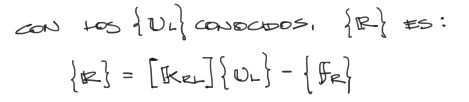
Aplicando este concepto al presente sistema, se tiene:

Y con los desplazamientos conocidos, se obtienen las reacciones:

El resultado es característico de una estructura en arco, donde los momentos flectores en la base (y en todo el arco, como se verá en la siguiente publicación) son casi nulos en comparación con las solicitaciones axiales.

Graficando desplazamientos

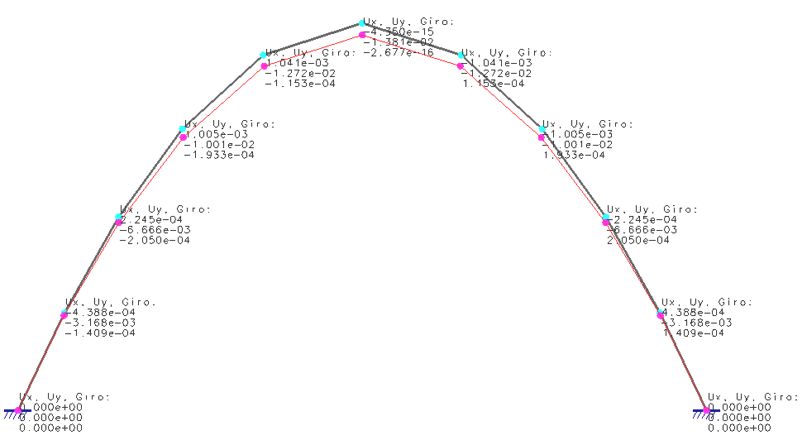
Los desplazamientos pueden graficarse magnificando las deformaciones de los elementos. En este caso escalaremos las deformaciones de los nudos 100 veces, para que se vuelvan apreciables. De esa manera, graficando el arco deformadoX100 Vs. sin deformar, se tiene:

Qué sigue

Los siguientes pasos del análisis consistirán en el cálculo de las solicitaciones de cada una de las barras y su respectiva graficación. Este último paso de análisis se lo verá en la siguiente publicación.

autor: Marcelo Pardo

←←← Arco Parabólico – Parte 1 ←←← →→→ Arco Parabólico – Parte 3 →→→

←←← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS ←←←