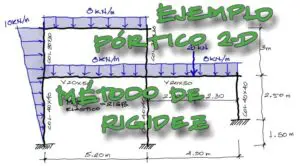
Enunciado
Se pide encontrar las solicitaciones internas de un arco parabólico de las dimensiones mostradas en la siguiente figura:
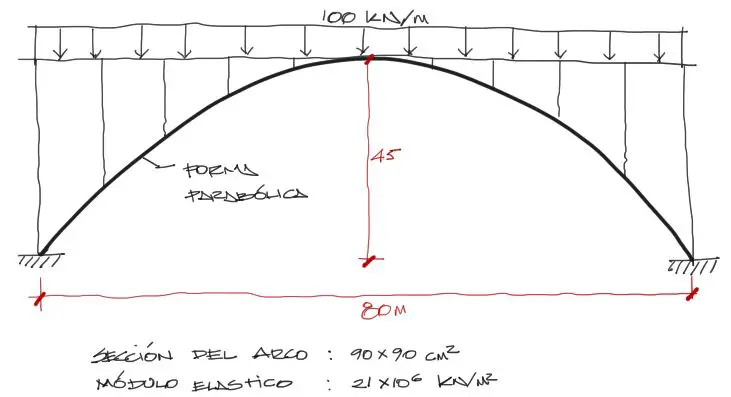
Las propiedades del arco son:
- Sección: 0.9m x 0.9m
- Peso propio del arco: no tomar en cuenta
- Apoyos: Empotrados
- Carga lineal del puente: 100 KN/m
Utilizar el método de rigidez para encontrar los desplazamientos y deformaciones del arco, reacciones y solicitaciones internas.
Resolución
Consideraciones iniciales
El proceso de resolución de las solicitaciones del arco pasa por encontrar primero la ecuación que describe la forma del arco. Posteriormente se discretiza el arco en partes casi iguales. Los tramos discretizados serán rectos describiendo solo aproximadamente la forma de la parábola.
Para acomodar la geometría de la parábola a la ecuación genérica de ésta, debemos referenciar la parábola al plano cartesiano:
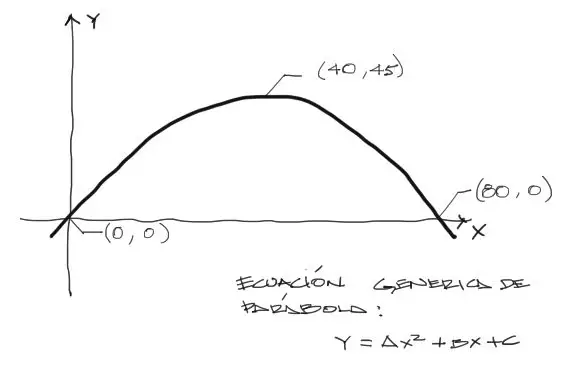
Si se reemplazan los 3 puntos señalados consecutivamente dentro de la ecuación de la parábola, se forma un sistema de 3 ecuaciones con 3 incógnitas, que se pueden resolver por cualquier método conocido.
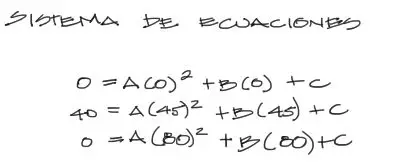
Resolviendo el sistema:

Geometría discretizada
El siguiente paso consiste en dividir el arco parabólico en partes más o menos iguales, de tal manera que las partes rectas se aproximen a la forma del arco. Se dividirá el arco en 10 partes.
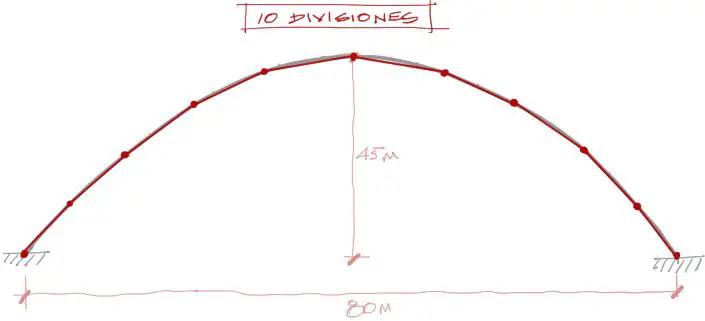
A critero se ubican puntos iniciales X para la discretización. Las coordenadas Y se obtienen con la ecuación de la parábola del punto anterior. Luego, por tanteos se van desplazando y cambiando las coordenadas en X de cada tramo, de tal manera que las longitudes de cada tramo (encontrado por pitágoras entre los puntos «i» y «i+1») sean más o menos iguales:
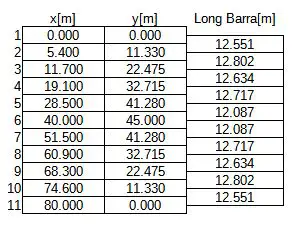
Las coordenadas proyectadas en la imagen se ven más o menos así:
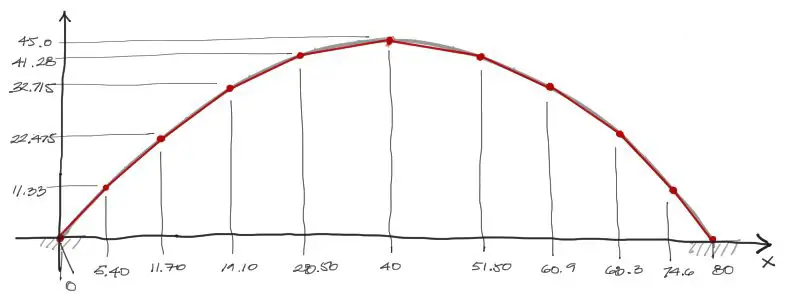
Matrices de rigidez
Con toda la información a la mano de la geometría de los elementos, junto con sus propiedades físico mecánicas, podemos encontrar las Matrices de rigidez de cada elemento según la teoría. Cada longitud de barra y ángulo de orientación puede encontrarse con las fórmulas:
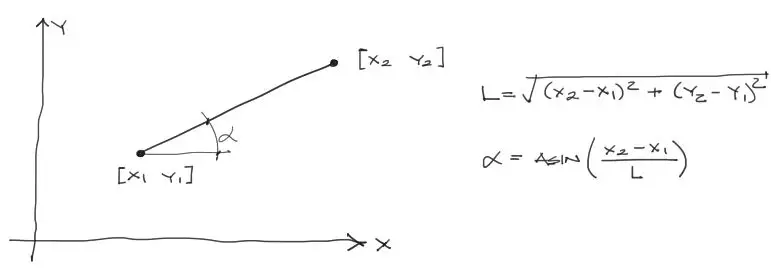
Además, el área de cada tramo es 0.9*0.9 = 0.81m2. La Inercia I= 0.9^4/12 = 0.054675m4. La fórmula de la matriz de rigidez de un elemento de pórtico es:
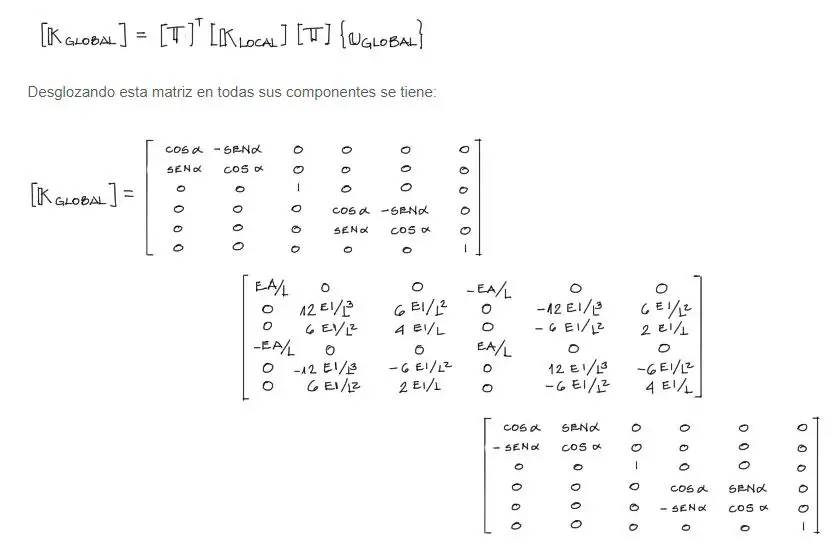
Reemplazando estos valores dentro de la fórmula de matriz de rigidez de pórtico para cada uno de los 10 tramos rectos:

En la lista de matrices mostrada se muestran además los grados de libertad correspondientes a cada barra según la numeración mostrada a continuación:
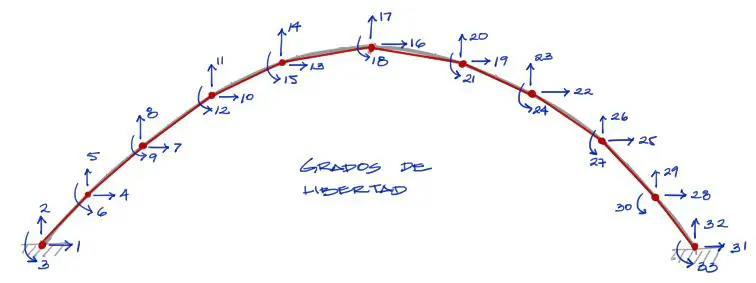
Matriz de toda la estructura
Encontradas las matrices de rigidez de cada barra, continuamos con el ensamblaje de la matriz de rigidez de toda la estructura. Para esto debemos transportar la matriz de rigidez de cada elemento en sus respectivos grados de libertad a la matriz de rigidez de toda la estructura que inicialmente estará llena de puro ceros.
Si dos celdas de diferentes elementos ocupan la misma posición dentro de la matriz de rigidez de la estructura, estos elementos se suman. Terminando el proceso de transporte de las matrices elementales hacia la matriz de la estructura, se tiene:

Esta es una matriz de 33×33 que contiene todos los grados de libertad de la estructura completa. En la siguiente publicación obtendremos el vector de fuerzas externas y la resolución del sistema de ecuaciones.
Autor: Marcelo Tomás Pardo Ayllón.