Antes de empezar

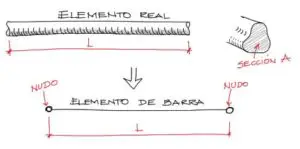
Antes de comenzar con el cálculo de los diagramas y cortantes de una viga, debemos recalcar que solo se puede aplicar el método una vez encontrados los desplazamientos en los estremos de una barra con dos nudos extremos.

La teoría de cálculo de desplazamientos en los nudos los puedes encontrar en los siguientes links:

• Matriz de rigidez de viga
• Ejemplo de resolución de viga por método de rigidez

Una vez que se tengan los desplazamientos en los nudos de cada barra, se procede con el análisis

¿Cuándo se utiliza este método?

El método se utiliza cuando terminamos de analizar los desplazamientos en los nudos de una viga resuelta por el método de elementos finitos o de rigidez.

En el método de elementos finitos es conveniente colocar nudos en los extremos de la viga, en los apoyos, donde existan cargas puntuales, y en todo sector donde aparezca un cambio bruzco en el tipo de carga.

Por tanto en un ejercicio típico de viga se podrán tener varios elementos de barra separados por nudos, como en el ejemplo del link mencionado anteriormente.

Resuelto el ejercicio se tendrán el desplazamiento vertical y el giro para cada nudo.

Mediante este método se podrá encontrar el diagrama de momento flector o cortante de cada barra entre dos nudos. Se deberá repetir el procedimiento para cada barra entre dos nudos de la viga.

Datos necesarios

El tramo de viga debe tener los siguientes datos:

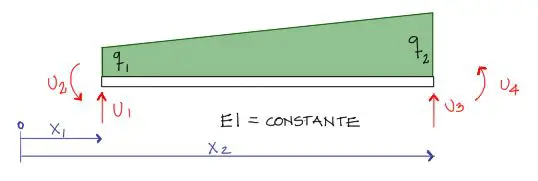
• u1 = desplazamiento vertical en el extremo izquierdo
• u2 = giro en el extremo izquierdo positivo antihorario
• u3 = desplazamiento vertical en el extremo derecho
• u4 = giro en el extremo derecho positivo antihorario
• x1 = coordenada del nudo izquierdo de la barra
• x2 = coordenada del nudo derecho de la barra
• q1 = valor de la carga distribuida en el extremo izquierdo de la barra
• q2 = valor de la carga distribuida en el extremo derecho de la barra
• ** q1 y q2 representan la carga distribuida positiva hacia abajo
• EI = rigidez del tramo

Se debe tener en cuenta que la carga distribuida mostrada representa el caso más general de cargas distribuidas. A partir de esta configuración se pueden generar cargas distribuidas de distinto tipo.

Demostración del Método

Ecuación de la recta de la carga distribuida

Lo primero que debemos hacer es conocer la ecuación de la carga distribuida a partir de las cargas q1 y q2 en los extremos. Para eso nos ayudamos de la teoría de geometría analítica donde encontramos los coeficientes A y B de la ecuación de la recta genérica mostrada:

En base a las coordenadas mostradas se forma un sistema de ecuaciones a partir del cual podemos encontrar los coeficientes A y B de la ecuación dela recta.

Despejando B de la primera ecuación y reemplazando la en la segunda podemos obtener los valores de A y B cómo se muestra:

En la ecuación mostrada se reemplazaron además los valores de A y B dentro de la ecuación de la recta.

Ecuación de la elástica de la viga

Ya es bien conocida la ecuación de la elástica de la viga pues la menciona en varias publicaciones anteriores. Partimos de esta ecuación para encontrar los diagramas de cortante y de momento flector.

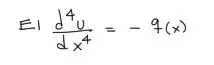
Se sabe de la teoría que al integrar esta ecuación 4 veces podemos encontrar todos los datos del cortante, momento flector, pendiente y deflexión de La viga:

De las anteriores ecuaciones la tercera derivada de la deflexión representa el cortante de la viga y la segunda derivada representa el momento flector.

Acto seguido se reemplazan las condiciones de contorno en las ecuaciones mostradas. En este caso las condiciones de contorno son los desplazamientos y giros en los extremos de la barra estudiada. En el extremo izquierdo para la coordenada x1 se tienen las condiciones de contorno de desplazamiento u1 y de giro u2. Una cosa similar sucede en el extremo derecho como se muestra a continuación:

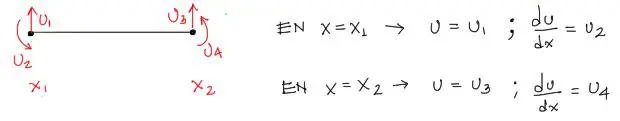
Ahora se reemplaza las condiciones de contorno dentro de las ecuaciones integradas de la elástica (tercera y cuarta ecuación) para obtener el sistema de 4 ecuaciones con 4 incógnitas. Las incógnitas en este caso son las 4 constantes de integración C1, C2, C3, C4

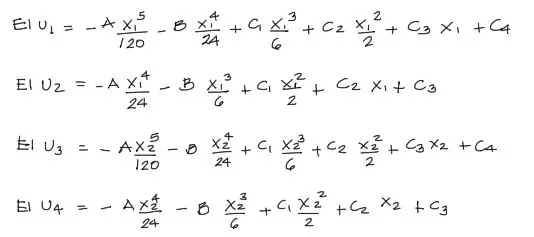
Hacemos los términos independientes llevándolos todos al extremo izquierdo de las ecuaciones:

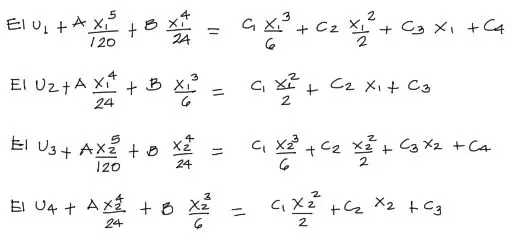
Ahora finalmente convertimos el sistema de ecuaciones a un arreglo matricial que puede resolverse por cualquier método numérico:

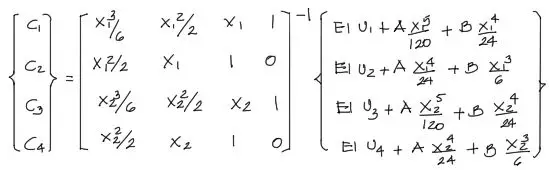
De las soluciones de este sistema de ecuaciones C1, C2, C3, C4 se pueden conocer y a las ecuaciones de cortante y momento flector para el tramo estudiado:

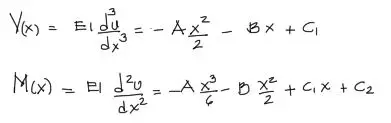
Se debe repetir el mismo procedimiento para todos los tramos que existan dentro de la viga.

Todo quedará mucho más claro con un ejemplo, que presento en el siguiente post y además en el vídeo mostrado a continuación:

FIRMAautor: Marcelo Pardo

← ← ← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS← ← ←