
Pasos previos
En anteriores publicaciones vimos como obtener las matrices de rigidez de cada elemento, la matriz de rigidez global de la estructura, y luego los desplazamientos y reacciones del arco. Los enlaces van a continuación:
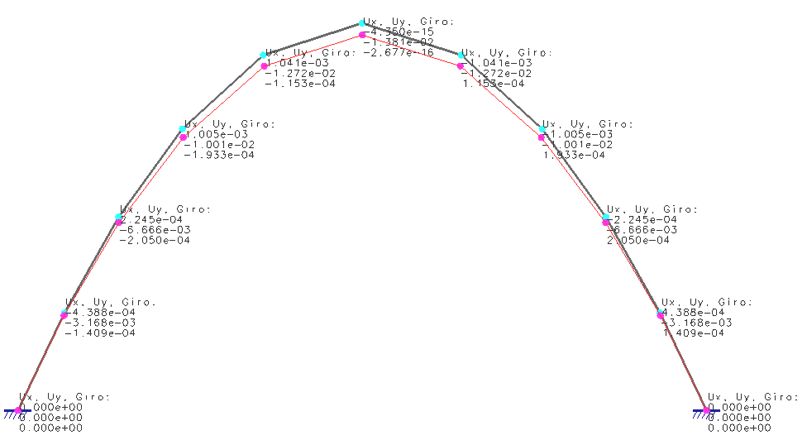
Solicitaciones de cada elemento
El proceso de cálculo de solicitaciones va de la mano con la teoría que puede encontrarse en Solicitaciones a partir de desplazamientos de los nudos.
En este caso en particular todas las barras del arco están rotadas cierto ángulo respecto a la horizontal, por tanto debemos seguir los siguientes pasos para encontrar las solicitaciones de la barra:
- a) Obtener (de cálculos anteriores) la matriz de rigidez en coordenadas locales de la barra
- b) Calcular la matriz de transformación [T] de la barra que está en función al ángulo de rotación
- c) Obtener los desplazamientos globales de los extremos de la barra {U_e}
- d) Calcular los desplazamientos de los nudos del elemento a partir de {U_e_local} = [T]*{U_e}
- e) Calcular las solicitaciones axiales de la barra
- f) Calcular las solicitaciones de M y V a partir del algoritmo de la teoría
a) Matriz de rigidez Ke en Coordenadas Locales
En la parte 1 de la resolución se calcularon las matrices de rigidez de cada elemento a partir de la fórmula:
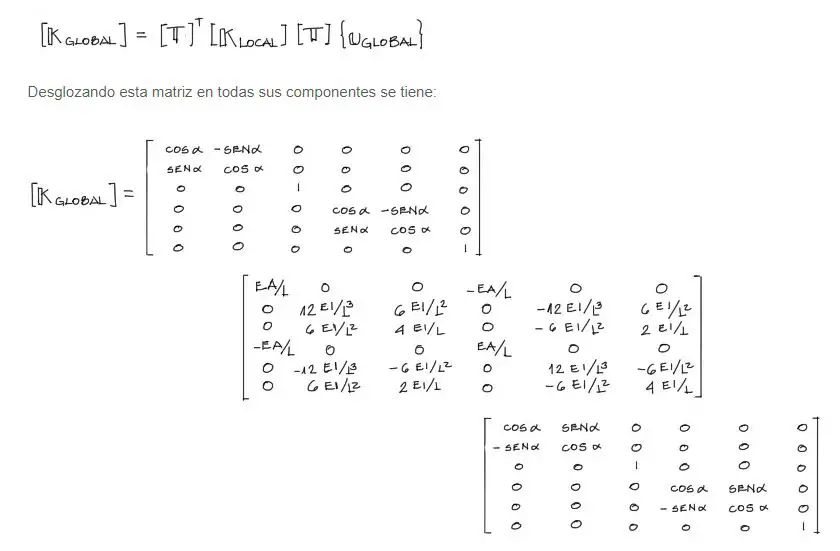
Por simplificar la presentación de los resultados, solo se mostraron en esa publicación las matrices [Ke] de cada elemento ya en coordenadas globales, o sea, el resultado de [K_e_local] premultiplicadas por [T]_transpuesta y post multiplicadas por [T].
En esta ocasión deberemos calcular [K_e_local] por un lado y posteriormente la matriz [T].
Para ejemplificar el análisis haremos todos los cálculos sobre el elemento 4 de nuestro arco. La longitud y ángulo de nuestro elemento son:

Con la Longitud de la barra, más los datos de sección A, inercia I, y módulo elástico calculamos Ke_local:
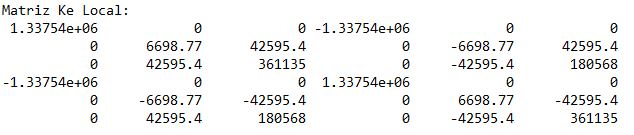
b) Matriz de transformación [T]
Con el ángulo de la barra 4, podemos calcular la matriz T:

Esta matriz nos ayudará a obtener los desplazamientos de los nudos de la barra 4 en coordenadas locales.
c) Desplazamientos globales de la barra 4
Los desplazamientos de la barra 4 están conformados por los grados de libertad 10, 11, 12 para el nudo inicial y 13, 14, 15 para el nudo final. Estos se resumen en la siguiente imagen:
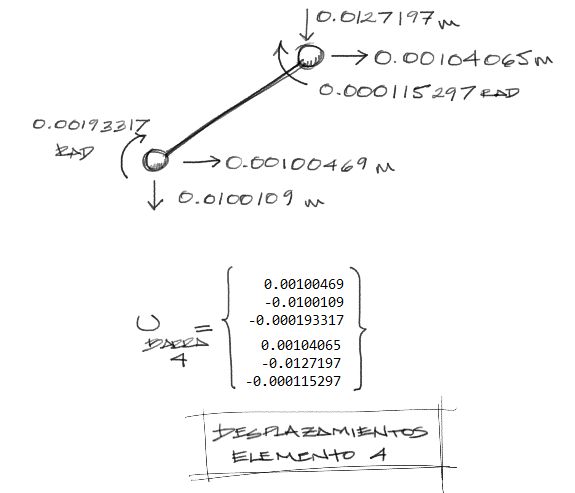
Estos desplazamientos como se muestran no nos sirven para el cálculo de solicitaciones de la barra. Para calcular las solicitaciones debemos transformar estos desplazamientos en desplazamientos locales.
d) Desplazamientos locales alineados con la barra
Estos desplazamientos están proyectados respecto a las coordenadas cartesianas globales de la estructura. Estos mismos desplazamientos pueden representarse en función a coordenadas locales alieneadas con la barra a partir de la matriz de transformación [T]. Para lograr esto multiplicaremos:

Luego, reemplazando valores:

E interpretando estos resultados para la barra 4, se tiene:

e) Solicitaciones axiales de la barra
Los desplazamientos locales 1 y 4 que coinciden paralelamente con el eje de la barra nos servirán para determinar la fuerza interna de compresión en la barra. Para eso:
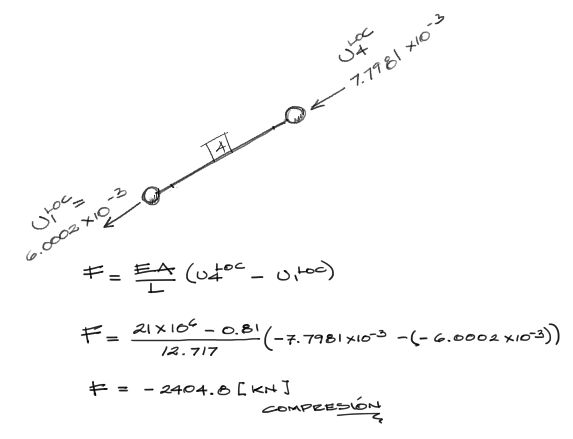
f) Solicitaciones de cortante y momento flector
Otra manera alternativa de obtener las solicitaciones axiales de la barra junto con las solicitaciones de cortante y momento, es a través de la matriz de rigidez en coordenadas locales que calculamos líneas arriba.
Si multiplicamos la matriz de rigidez local por los desplazamientos locales, obtenemos directamente todas las solicitaciones de la barra:

Reemplazando los datos de KeLocal y de Ulocal se tiene:

Operando e interpretando los resultados se tiene:
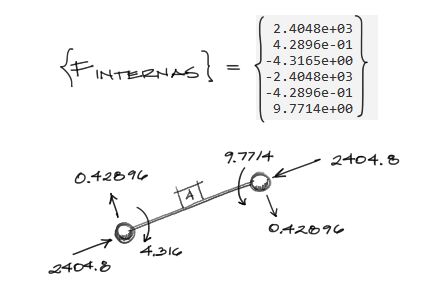
Como se puede apreciar, tanto solicitaciones de momento M y cortante V son residuales comparadas con las solicitaciones axiales N de la barra. Esto era de esperar gracias a la naturaleza del arco que distribuye las fuerzas verticales a través de solicitaciones predominantemente axiales.
Repitiendo para toda la barra
Automatizando el proceso para el resto de los elementos se tienen las solicitaciones siguientes:
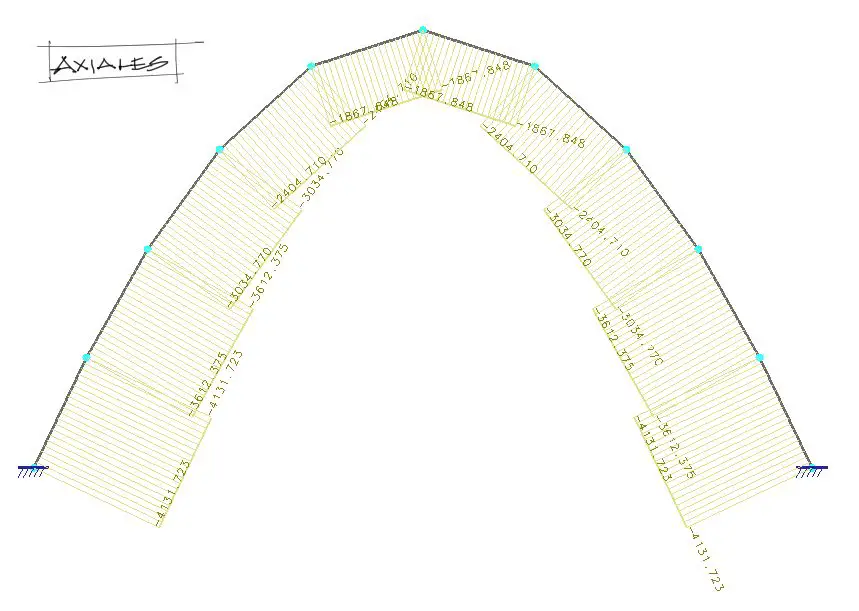

autor: Marcelo Pardo


Gracias Marcelo, por tu pronta respuesta; perdón por la insistencia, pero en todo el ejercicio no fue necesario recurrir a dicha ecuación porque discretizamos la parábola con varios elementos de barra. ¿Estoy correcto? Gracias nuevamente y saludos.
Y cómo encuentras los puntos discretizados sin la ecuación de la parábola? 🙂
De todas maneras tienes razón en algo. no está clara la explicación. Acabo de hacer la aclaración en el punto pertinente para que se entienda mejor.
Muchas gracias!!
¡Cierto!! ¡Acabo de comprender!! Gracias Marcelo, agradezco tu atención y paciencia! Saludos!
Un gusto ayudar Alberto! Gracias por visitar el sitio Web
Estimado Marcelo: perdón, a lo mejor no revisé bien, pero ¿para qué nos sirvió encontrar la Ecuación de la Parábola en la Parte 1 del ejercicio? Gracias y saludos.
Alberto, es porque en el enunciado solo nos dan 3 puntos por donde pasa el arco.
Luego encontramos la ecuación para tener el resto de los puntos para poder trazar el modelo matemático