Planteamiento del Problema
En hormigón armado se platean siempre dos tipos de análisis:
– Se requiere diseñar una sección de viga en función a las solicitaciones.
– Se requiere verificar la resistencia de la sección de viga para compararla con las solicitaciones.
La primera de las opciones se analiza en otra publicación cuyo enlace es Diseño de vigas sin acero a compresión.. Por otro lado, en esta publicación nos dedicaremos a analizar la segunda opción de verificación de la resistencia a flexión de una viga (que puede estar ya construida).
Datos del problema
Cuando se verifica una viga, las dimensiones de la viga, cantidades de acero y las resistencias son conocidas, por tanto los datos son:
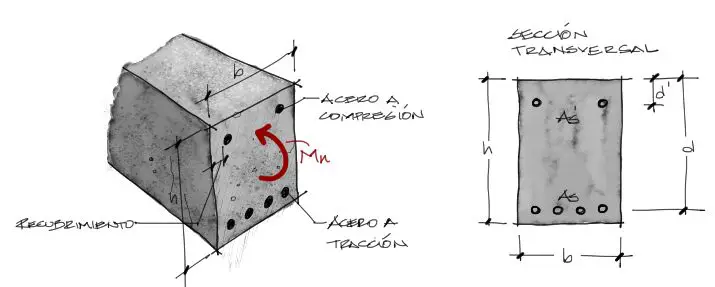
- Ancho de la viga «b»
- altura de la viga «h»
- recubrimiento al eje de aceros a compresión «d'»
- distancia efectiva de la fibra más comprimida al eje de aceros a tracción «d»
- Cantidad de acero a compresión «As'»
- Cantidad de acero a tracción «As»
- resistencia característica a compresión del concreto «fc'»
- resistencia a fluencia del acero «fy»
A partir de todos estos datos debemos determinar la resistencia a flexión de la viga. Para este propósito, encontraremos un primer parámetro de la viga que nos servirán para saber cómo y cuando falla la viga. Este parámetro se llama cuantía balanceada.
Paso 1: Cuantía balanceada cuando la viga no tiene As’
Entre los datos necesarios para conocer el comportamiento de la viga, debemos conocer la cantidad de acero a tracción que logra que tanto acero a compresión como a tracción fluyan al mismo tiempo. Este dato marca una frontera con la que podremos determinar si la falla de la viga es frágil o es dúctil. Si la viga no lleva acero a compresión (As’= 0) y la cantidad de acero a tracción es menor al de la cuantía balanceada, entonces la viga tendrá una falla dúctil. Al contrario si la viga no lleva acero a compresión y As es mayor a Asb, la falla será frágil debido a la explosión del hormigón.
Para determinar la cantidad de acero que logra la falla balanceada, asumimos que tanto acero como concreto llegan a la fluencia:
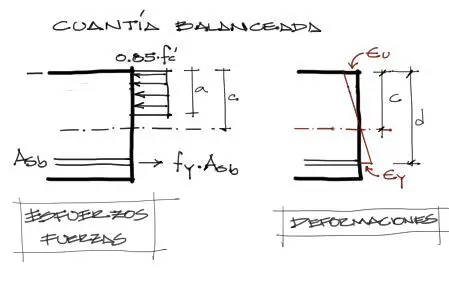
A la izquierda se tienen dibujados los esfuerzos involucrados en la sección transversal. A la derecha se muestran las deformaciones unitarias en fluencia o falla de la sección transversal. En estas gráficas,
a: altura efectiva del bloque de compresión
c: altura del eje neutro
Asb: sección de acero correspondiente a la cuantía balanceada
ξu: deformación unitaria del concreto en falla e igual a 0.003
ξy: deformación unitaria del acero en fluencia
Si hacemos la suma de fuerzas del esquema de la izquierda logramos el equilibrio de la sección transversal.
En la primera ecuación son desconocidos «Asb» y «a». Para encontrar «a» existe una variable β1 que relaciona «a» con la altura del eje neutro «c» (el cálculo de β1 lo encuentras en el Algoritmo de diseño de acero a flexión. Luego reemplazando a = β1*c y despejando Asb de la primera ecuación se tiene la expresión mostrada. Nuevamente de esta ecuación no se conoce el acero balanceado «Asb» ni la altura del eje neutro «c».
La altura del eje neutro la podemos encontrar a partir de las deformaciones dibujadas arriba. Por relación de triángulos podemos relacionar la deformación unitaria del concreto y acero, ambos en fluencia, con la altura del eje neutro C:
Esta altura del eje neutro C encontrada la reemplazamos en la ecuación de equilibrio de fuerzas y así obtenemos la sección de acero balanceado:
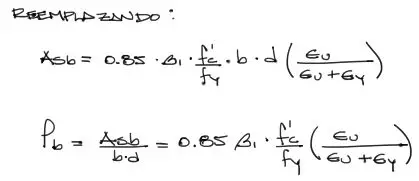
La expresión arriba se puede expresar también en términos de cuantía balanceada, dividiendo el acero balanceado entre la sección efectiva de la viga b*d.
Paso 2: Cuantía balanceada cuando la viga tiene acero a compresión
Rara vez una viga no lleva acero en la cara comprimida. Por lo general, incluso si fuera acero constructivo para el amarre de estribos, las vigas llevan acero en la cara comprimida. En todos esos casos debemos incluir el acero a compresión dentro de las fórmulas de la cuantía balanceada. Denotando al acero a compresión como As’, tenemos:
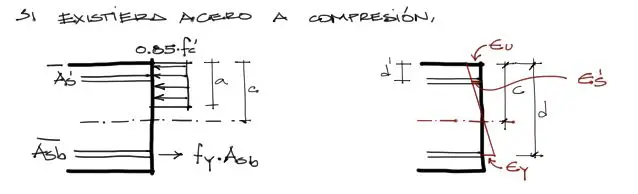
Y equilibrando nuevamente las fuerzas horizontales, se tiene:
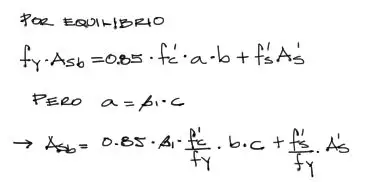
Por definición estamos calculando la cantidad de acero a tracción que logra la fluencia de As como fc’. Es por eso que As se multiplica por el esfuerzo de fluencia fy. Sin embargo con el acero a compresión no sucede lo mismo, ya que no sabemos si el acero a compresión fluye. es por eso que As’ está multiplicado por fs’ y no por fy. Esta es una nueva incógnita que debemos resolver a partir de las deformaciones de la sección transversal dibujada arriba.
Del diagrama de compatibilidad de deformaciones podemos encontrar la altura del eje neutro C, y además por relación de triángulos también podemos encontrar la deformación unitaria del acero a compresión ξs’ a partir de todos los otros datos conocido.
El esfuerzo fs’ entonces se encuentra por resistencia de materiales σ = E*ξ. Si fs’ es mayor a fy, se asume fs’=fy introduciendo fy en vez de fs’ en la fórmula de equilibrio de fuerzas pues el acero a compresión fluye. De otra manera, si fs’ es menor a fy, fs’ ingresa en la fórmula de equilibrio.
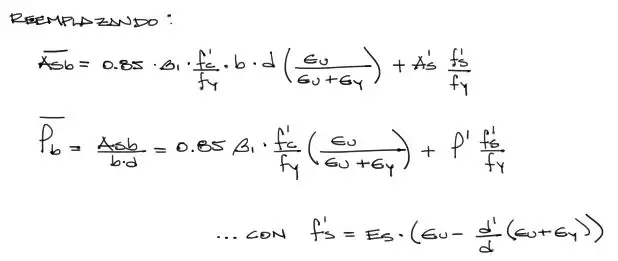
Esta es la fórmula final de cantidad de acero que logra que tanto acero como hormigón fluyan al mismo tiempo. Esta fórmula marca una de las fronteras para las 4 alternativas de cálculo posterior.
¿Acero a tracción Fluye o no?
La cuantía balanceada es una propiedad de la viga que marca una frontera entre si el acero fluye antes que el concreto o viseversa. Sin ambargo, una viga casi nunca está armada con una cantidad de acero igual al de la cuantía balanceada. La viga en estudio por lo general tendrá menos cantidad de acero que el balanceado, aunque en algunos casos tendrá más.
Cabe entonces preguntarnos. ¿La cantidad real de acero en la viga tendrá más o menos acero que el de la cuantía balanceada?. En función a esta condición seguiremos uno de dos caminos:
- El acero real As es menor al Acero balanceado Asb: ρ menor a ρb
- El acero real As es mayor al Acero balanceado Asb: ρ mayor a ρb
autor: Marcelo Pardo
