Antecedentes
Hasta este punto ya se tiene que tener armada la matriz de rigidez global de la estructura [K]. Se forma entonces el sistema de ecuaciones mostrado en la figura, con vectores y matrices escritos de forma abreviada.
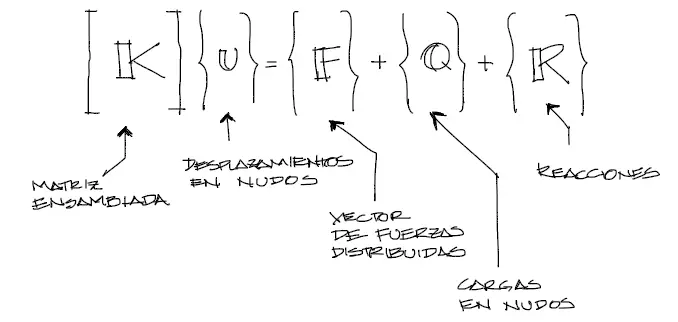
Dónde los términos del sistema corresponden a:
– [K] = Matriz de rigidez ensamblada de toda la estructura
– {u} = Vector de desplazamientos de los nudos
– {F} = Vector de fuerzas equivalentes en los nudos a partir de cargas distribuidas
– {Q} = Cargas puntuales o momentos de fuerza aplicadas directamente en nudos
– {R} = Vector de reacciones en los nudos restringidos con desplazamiento cero.
En este artículo me dedicaré a explicar entonces la manera de armar el vector de cargas puntuales {Q}
Vector de Cargas Puntuales
Al momento de calcular un pórtico por el método de rigidez, lo más conveniente es crear nudos en los siguientes casos:
– En los apoyos de la estructura
– En las intersecciones entre dos o más elementos de barra
– Donde existan cargas puntuales en medio de elementos de barra
– donde existan momentos de fuerza en medio de elementos de barra
Los dos primeros puntos enumerados son obvios pues cualquier cambio de dirección de la barra o intersección entre dos barras generará un nudo. De la misma manera los puntos donde terminan los pórticos, por naturaleza de la barra deberán tener otro nudo.
Sin embargo los otros dos puntos de la lista no son tan obvios. El motivo por el cual es mejor crear un nudo en los puntos de aplicación de cargas en algún punto en medio de elementos de barra es porque solo de esa manera se puede obtener la precisión adecuada al momento de calcular los desplazamientos o de dibujar los diagramas de momento y cortante.
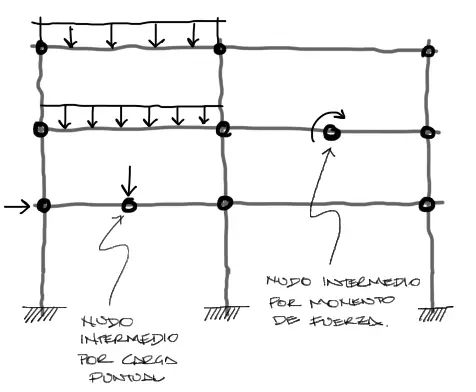
Es cierto que si no se creara este nudo intermedio, igual se puede cargar la estructura a partir de cargas equivalentes en los nudos de los extremos de la barra pero esto trae inconvenientes. Por un lado reduce la precisión del cálculo de desplazamientos en los nudos y en consecuencia reduce la precisión del cálculo de solicitaciones, y por otro lado hace difícil la graficación de momentos y cortantes pues para un tramo de barra suele contarse sólo con una ecuación de graficación de momentos y una de cortantes. El hecho de que exista una carga puntual al centro de un tramo de barra, genera una discontinuidad en las ecuaciones de momento y cortante y por tanto, la necesidad de más de una ecuación para cada solicitación.
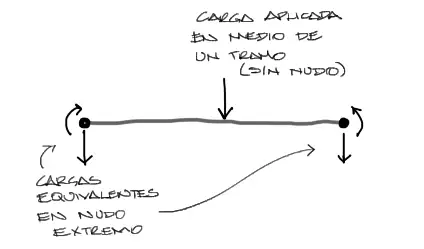
Este procedimiento de transformar una carga al centro del tramo en cargas puntuales equivalentes en los nudos se reserva casi exclusivamente para cargas distribuidas, cuyo análisis se verá en la siguiente publicación.
Grados de libertad
Por fortuna, las cargas puntuales son fáciles de aplicar. Solo debe hacerse coincidir el grado de libertad del nudo con la carga aplicada, y transportar la magnitud de esta carga a la posición dentro del vector de cargas Q, tal como se muestra en la imagen siguiente. Para los nudos no cargados, el valor de la carga es simplemente cero.
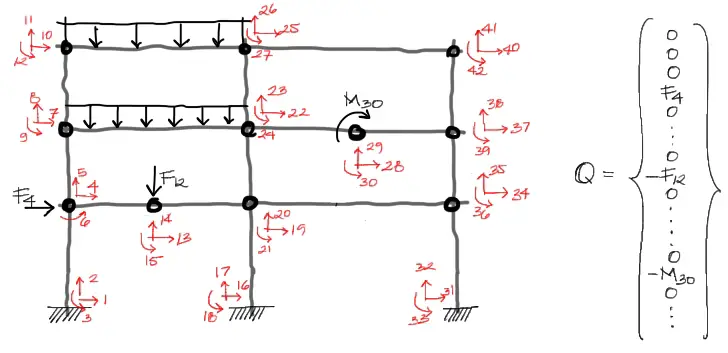
Se debe tomar en cuenta que la dirección de la carga es positiva en el vector de cargas Q si coincide con la dirección positiva del grado de libertad. Negativa de lo contrario. Convencionalmente las fuerzas globales serán positivas si apuntan en la dirección derecha, arriba, o momentos en sentido antihorario.
autor: Marcelo Pardo