Concepto

Todo vector, independientemente de lo que represente, tiene un vector unitario correspondiente.

Los vectores unitarios son vectores que tienen la misma dirección y sentido que el vector original, pero cuya magnitud es igual a uno. Dicho en términos sencillos, un vector unitario apunta en la misma dirección que el vector original pero tiene magnitud uno.

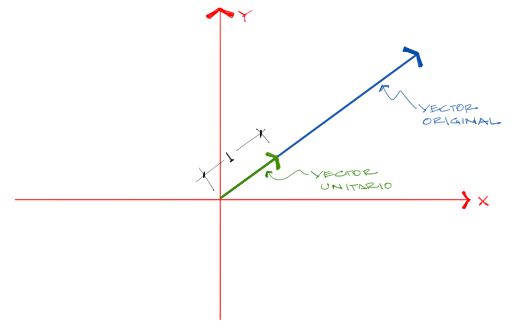
Otra característica principal de los vectores unitarios es que no tienen unidades, como se demostrará a continuación.

Fórmulas

Si el vector original A tiene componentes [Ax, Ay] y tiene magnitud |A|, entonces las componentes del vector unitario u son:

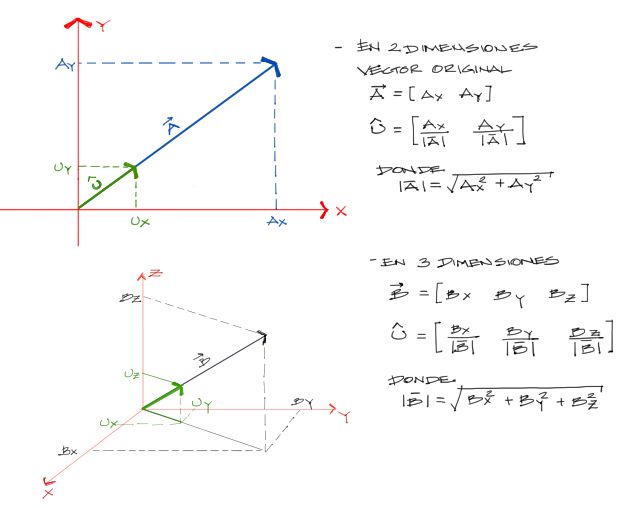
Como se puede ver en la fórmula de vector unitario, tanto el numerador como el denominador tienen las unidades del vector original, que se anulan en el cálculo del vector unitario. Es por esto que se indicó arriba que el vector unitario no lleva unidades.

Esta última característica hace que se pueda combinar el uso de los vectores unitarios junto con vectores posición para luego, por ejemplo, conocer las componentes de un vector fuerza, a partir del vector unitario obtenido. Este ejemplo se verá más adelante.

Programa 1 (componentes)

Introducir las componentes de un vector A en 2 o 3 dimensiones. El programa calculará su vector unitario. Si el vector es en 2 dimensiones, Z=0

Programa 2 (Magnitud y dirección)

Introducir la magnitud y dirección del vector cuyo vector unitario se quiere obtener. Recordar que la dirección se debe medir desde el eje X positivo y antihorario positivo (horario negativo).