Introducción
Los elementos de cercha son elementos que se deforman axialmente pero en un plano en 2D. Para conocer el comportamiento de elementos con deformación axial en una dimensión puedes consultar el link matriz de rigidez de elementos con deformación axial 1D
La única diferencia es que estos elementos de cercha necesitan una transformación de coordenadas para funcionar en 2 o en 3 dimensiones.
Esta transformación de coordenadas de 1-D a 2-D genera en cada nudo, un grado de libertad extra (en total dos grados de libertad por nudo). En el caso de transformación de coordenadas de 1-D a 3-D se generarán 2 grados de libertad adicionales para cada nudo (con un total de 3 grados de libertad).
Demostración
Arrancamos con el elemento de cercha mencionado en el artículo anterior. El elemento cuenta con un grado de libertad por nudo, como se muestra a continuación:
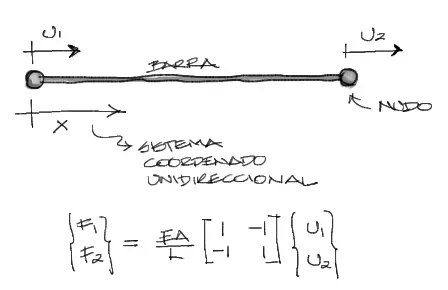
Para que este elemento expuesto a deformaciones axiales pueda trabajar en un espacio bidireccional, lo rotaremos un ángulo alfa. De tal manera, se generan en cada nudo dos grados de libertad en un sistema global de coordenadas.
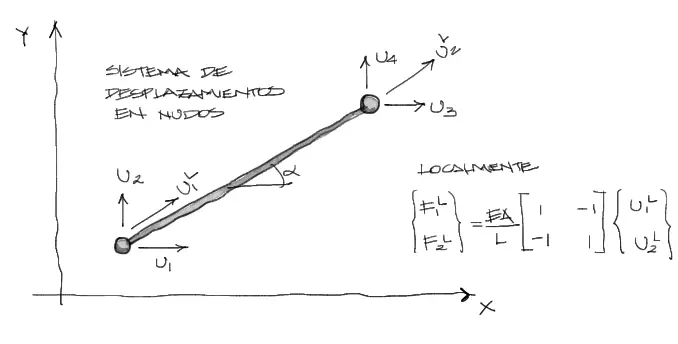
Nota que los desplazamientos en coordenadas globales no llevan superíndice mientras que los desplazamientos en coordenadas locales llevan el superíndice “L”.
En lo que consiste el trabajo a continuación es en buscar una relación entre el desplazamiento local U1L y los desplazamientos globales U1 y U2. De la misma manera con el otro nudo.
Así como se busca realizar la transformación de los vectores desplazamiento de locales a globales, lo mismo pasa con las fuerzas, de locales a globales:
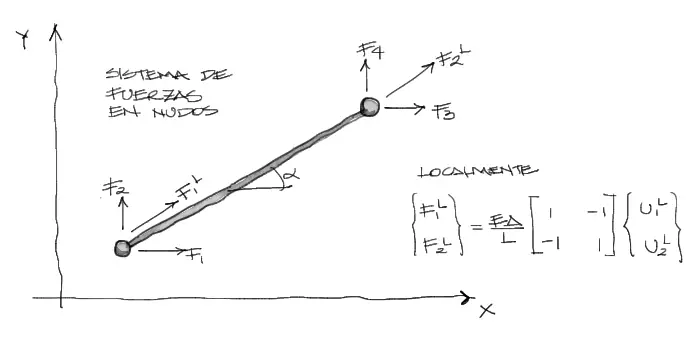
Transformación de coordenadas de Desplazamientos
Centrándonos en el nudo izquierdo del elemento rotado. Si descomponemos los desplazamientos globales U1 y U2, se tiene lo siguiente:
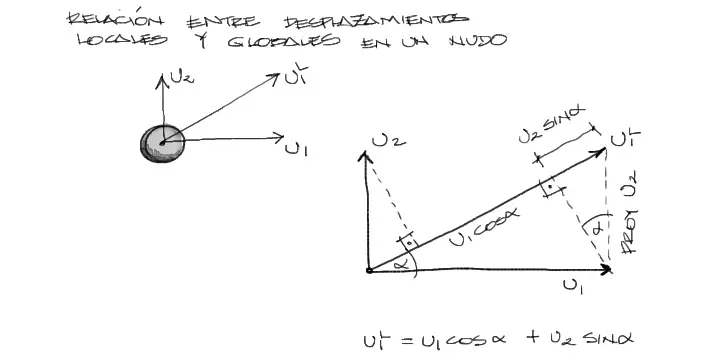
U1 Local puede componerse por las proyecciones de los desplazamientos U1 y U2 sobre U1Local.
Repitiendo el procedimiento para los desplazamientos del otro nudo, se obtienen las dos siguientes ecuaciones:
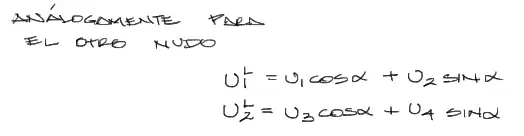
Escribiendo lo anterior en forma matricial, se tiene:
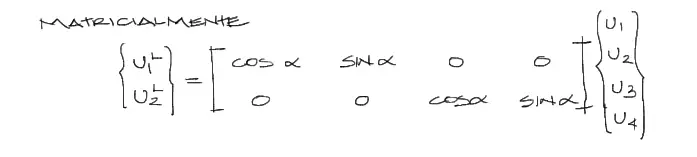
Finalmente toca reemplazar los desplazamientos en coordenadas locales, por los desplazamientos en coordenadas globales. Este reemplazo debe hacerse en el sistema de ecuaciones que relaciona desplazamientos con fuerzas externas, de la siguiente manera:
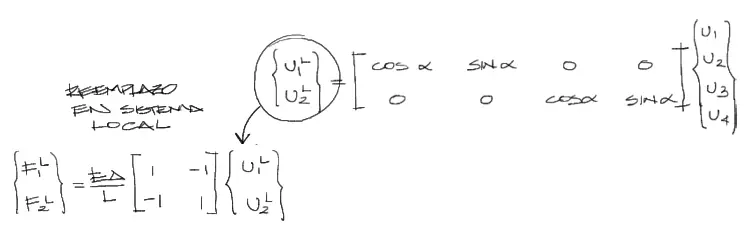
El sistema de ecuaciones anterior entonces queda:
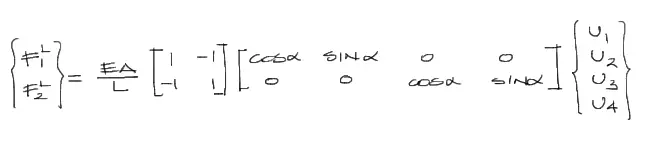
Transformación de coordenadas de fuerzas externas
De manera similar a los desplazamientos, ahora nos enfocamos en las fuerzas en los nudos. Las fuerzas locales llevan el superíndice L mientras que las fuerzas en coordenadas globales no llevan estos superíndices.
Si nos concentramos en las fuerzas del nudo izquierdo se tiene lo siguiente:
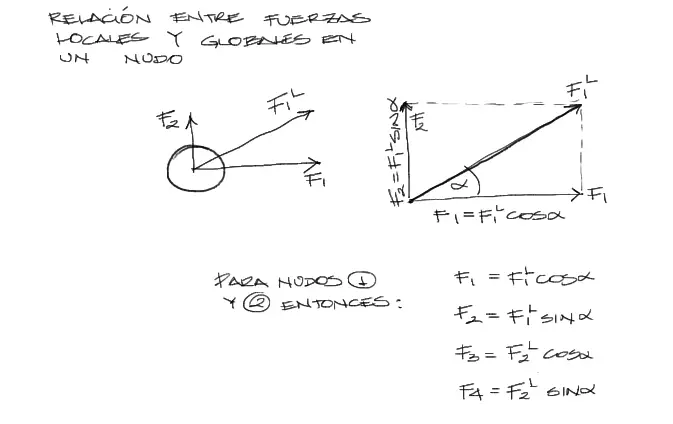
Esta vez descompondremos las fuerzas locales en su respectiva proyección sobre los ejes X e Y globales. De esta manera, por ejemplo la proyección de F1L sobre el eje X es F1L*cos(alfa) y este resoltado es la fuerza X en coordenadas globales para este nudo. Repitiendo el proceso para X y Y para ambos nudos, se tienen las fórmulas en la imagen anterior.
Escribiendo estas fórmulas en coordenadas en forma matricial se tiene:
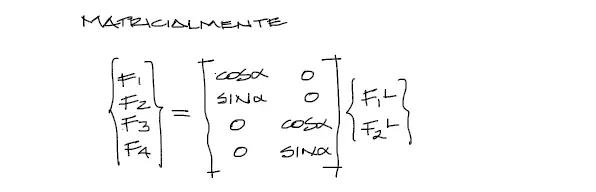
A diferencia del procedimiento realizado a estas alturas con los desplazamientos, ahora reemplazaremos las fuerzas locales de la ecuación Desplazamientos-Fuerzas, dentro del último sistema de ecuaciones obtenido, de la siguiente manera:
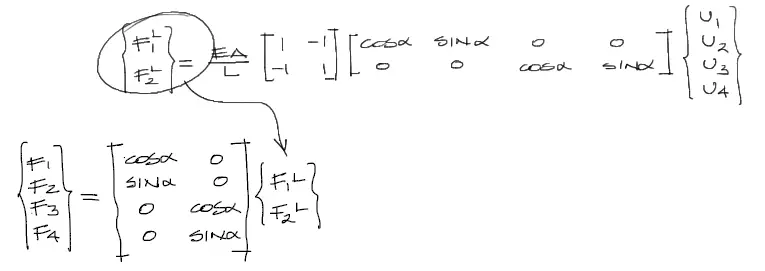
Así, tenemos el sistema que relaciona desplazamientos con fuerzas completo. Reescribiendo el sistema final se tiene:
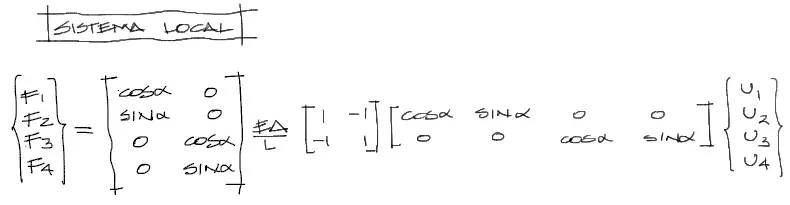
De la anterior ecuación, la matriz de rigidez para un elemento de cercha es la siguiente:
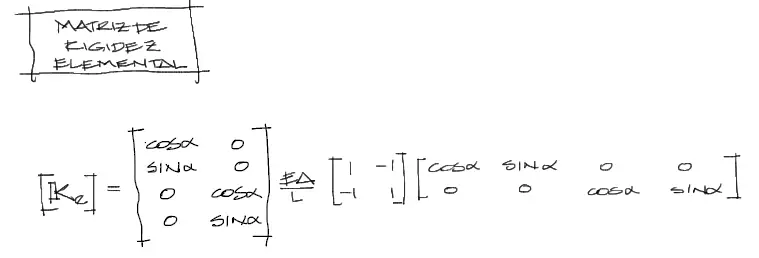
Procedimiento de análisis
Una vez obtenido el sistema anterior, el procedimiento de análisis de cerchas va como sigue:
- Numerar cada barra, cada nudo, y cada grado de libertad
- Encontrar L,A,angulo,E de cada barra
- Encontrar la matriz de rigidez de cada barra
- Ensamblar las matrices de rigidez elementales en una Matriz de toda la estructura
- Establecer las condiciones de contorno y cargas
- Reducir el sistema de ecuaciones de toda la estructura según las condiciones de contorno
- Resolver los desplazamientos
- Resolver las reacciones de los apoyos
- Encontrar las solicitaciones de cada barra en función a los desplazamientos en los nudos de cada barra
Si bien en este procedimiento de analisis se mencionan los pasos de forma muy general, en el siguiente artículo se explica con un ejemplo el uso de la matriz de rigidez mencionado acá./p> FIRMA
autor: Marcelo Pardo

