Enunciado
Se pide determinar la magnitud de la fuerza resultante F1+F2 y su dirección. La dirección debe estar medida en el sentido positivo antihorario a partir del eje X. (El ejercicio fue sacado del libro Hibbeler (Ej.2-1)
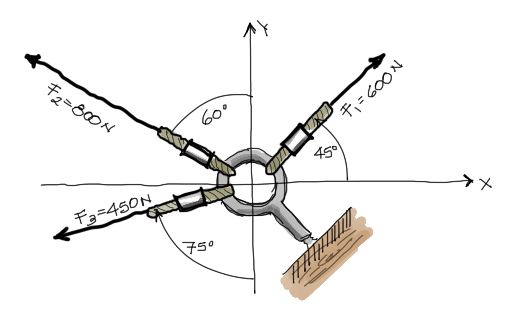
Solución por Trigonometría
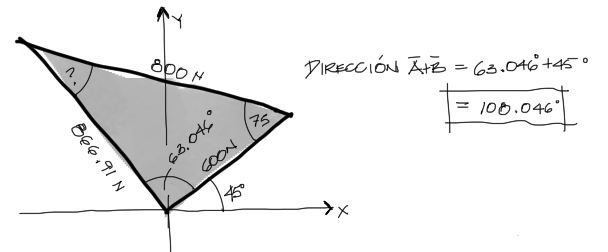
Nota que en primer lugar, el ejercicio no menciona ni requiere el uso del vector F3 mostrado, por tanto no lo tomamos en cuenta. A partir de los vectores F1 y F2, aislando los vectores del gráfico de la argolla queda:
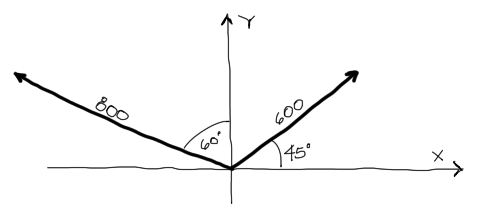
Posteriormente debemos formar un arreglo punta-cola como en la explicación de Teoría de suma de vectores por ley de senos y cosenos. Del triángulo formado veremos cuales datos nos faltan para llegar a la respuesta del enunciado. Entonces con un arreglo punta cola F1 + F2 se tiene:
El siguiente paso consiste en encontrar los ángulos internos del triángulo. Para esto necesitamos un poco de ingenio y deducir donde se repiten los ángulos y donde se complementan:
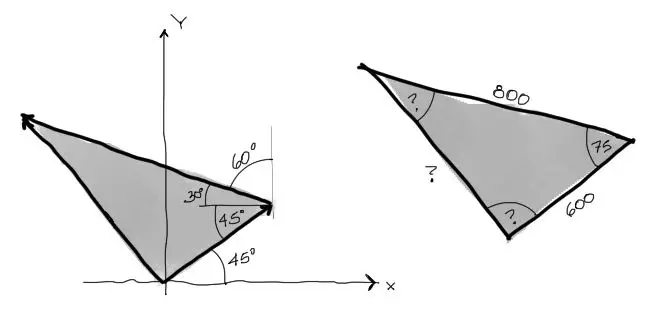
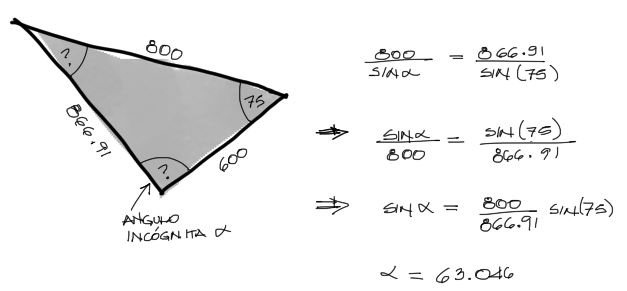
Como se ve en el gráfico tenemos tres datos y tres incógnitas. El lado incógnita puede resolverse mediante ley de cosenos pues conocemos los otros dos lados y el ángulo frente al lado incógnita. Entonces tenemos:
Una vez conocida la magnitud del lado incógnita A+B, ahora por ley de senos podemos averiguar el ángulo que se forma entre el vector A y el vector resultado A+B:
El enunciado pide el ángulo medido desde el eje de las X en el sentido antihorario, por tanto deducimos tal ángulo a partir de la suma del ángulo alfa encontrado más 45°:
Solución por componentes (Verificación)
Mediante la descomposición de los vectores, el procedimiento suele ser más mecánico. Entonces primeramente descomponemos cada vector a partir del módulo y el ángulo que forman con la horizontal y vertical:
Luego podemos sumar componentes. Existen dos notaciones para la escritura de vectores. Adoptaremos en este caso la notación en base a vectores unitarios:
Luego encontramos la resultante o la magnitud del vector resultante A+B a partir de pitágoras.
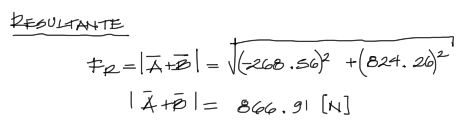
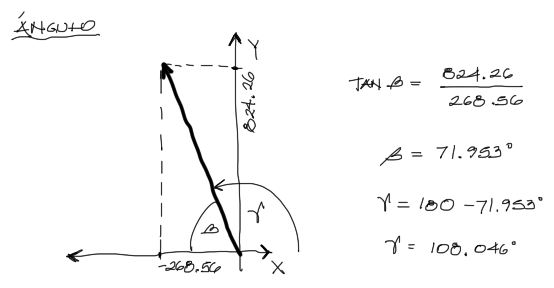
Este resultado está en Newtons [N] al igual que todos los vectores aplicados. El módulo o resultante de un vector siempre siempre será Positivo. Finalmente para obtener el ángulo, se calcula primero el ángulo beta mediante la fórmula de Tangente. Obtenido este valor se calcula gamma a partir del complemento del ángulo beta.
autor: Marcelo Pardo
