Continuación

En la primera parte de esta publicación vimos como obtener las deformaciones en los nudos en una viga tradicional de 3 tramos con los 3 tipos de carga más usuales dentro de la ingeniería Civil. (puntual, triangular y rectangular).

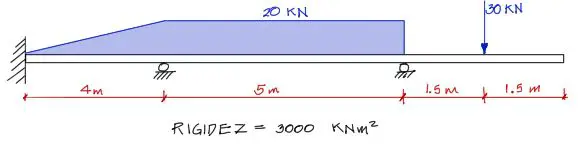
El procedimiento de la viga cuyas deformaciones se encontraron lo puedes encontrar en Viga de 3 tramos – deformaciones en nudos. La viga es la que se muestra en la imagen siguiente:

Una vez analizados los desplazamientos, los resultados encontrados fueron los siguientes:

En la gráfica, los desplazamientos verticales son impares y los giros en radianes, pares.

Postproceso

El método de elementos finitos o de rigideces termina justo en la anterior imágen. Lo que sigue es aplicar conocimientos de teoría de vigas y de resistencia de materiales para encontrar los diagramas de momentos flectores y cortantes de la viga. Esta teoría la puedes encontrar en el siguiente link de Cortantes y Momentos a partir de desplazamientos en los nudos.

Análisis de tramo 1

Una vez que le hayas echado un vistazo a la teoría, te darás cuenta que el procedimiento es bastante mecánico. Vamos aplicando la fórmula final en forma matricial de la teoría mencionada, como sigue:

En el tramo 1, las coordenadas de los extremos de la barra son 0.0 y 4.0 respectivamente. q1 y q2 son las magnitudes de la carga distribuida en los extremos del tramo. Si la carga fuera puntual, tanto q1 como q2 serán cero, como se verá en los últimos dos tramos.

Finalmente debido a las condiciones de empotramiento a la izquierda y de apoyo restringido a los desplazamientos a la derecha de la barra, todos los desplazamientos son nulos excepto en el GDL 4 (GDL = grado de libertad).

Reemplazamos primeramente q1 q2 x1 x2 en las fórmulas de A y B para luego insertarlas en la matriz

Reemplazando luego todos los datos en la matriz, se tiene:

Y así encontramos rápidamente las constantes C1 C2 C3 C4. ¿Qué hacemos con estas constantes? las reemplazamos en las ecuaciones de cortante y de momento flector también explicados en la teoría. Estas ecuaciones se obtienen a partir de la integración de la ecuación de la elástica de la viga.

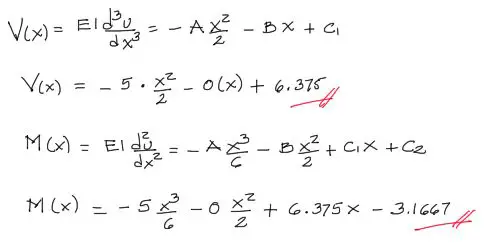
Quiero que recuerdes estas ecuaciones para la graficación final de los diagramas.

Análisis de tramo 2

De la misma manera que en tramo 1, reemplazamos los datos de este tramo, tanto de cargas, coordenadas como de desplazamientos en la matriz de las constantes. Se tiene entonces:

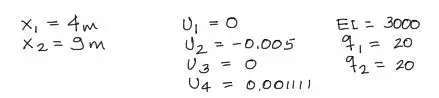
El procedimiento es el mismo del anterior tramo, con la única diferencia de que esta vez los nuevos x1 y x2 son los de las coordenadas del segundo tramo. Además, los desplazamientos que en la viga corresponden al segundo tramo, u3 u4 u5 u6, deben re-enumerarse para convertirse en u1 u2 u3 u4 para entrar dentro de la matriz para encontrar las constantes.

Reemplazamos pues, todos los datos de este tramo en la ecuación: br

donde A = 0 y B = 20. Se tiene como resultado entonces:

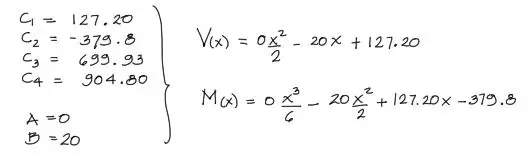
Análisis de Tramo 3

A pesar de que la viga es solo de tres tramos, se tuvo que colocar un nudo en el lugar de la carga puntual pues ésta genera una discontinuidad tanto en los diagramas de momento flector como de cortante. Entonces en términos de elementos utilizados, este sería el tercer tramo de 4 tramos.

Los datos para este tercer tramo son los siguientes:

Notarás que para este tramo, las cargas q1 y q2 son cero, como mencioné al comienzo de la publicación. Esto se debe a que estos valores representan solamente las magnitudes de la carga distribuida del tramo. Para cargas puntuales, que son solo discontinuidades en el diagrama de cortantes, la carga no figura.

Análisis del tramo 4

Este es el último tramo a la derecha de la carga. Éste es el único tramo donde ninguno de los desplazamientos o giros son cero. Al igual que en el anterior tramo, no existe carga distribuida y por tanto q1 y q2 son cero. Los datos son los siguientes:

Nota que en este tramo, debido a que en el extremo del voladizo no existe ninguna carga, tanto cortante como momento flector son cero.

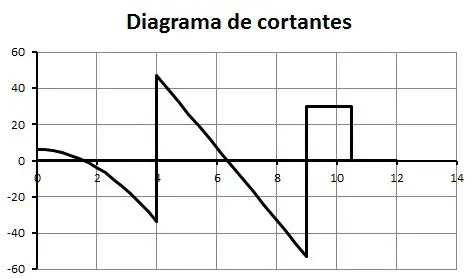
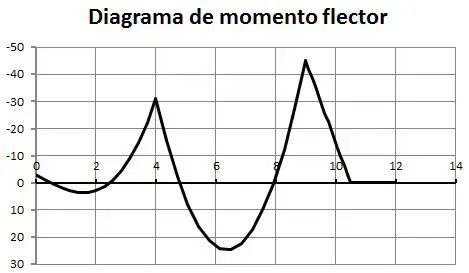
Diagramas de cortante y momento flector

Resumiendo todas las ecuaciones de momento flector encontradas hasta el momento, tenemos para los cuatro tramos:

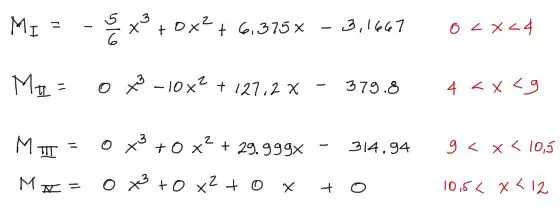
Con estas ecuaciones de momento flector se pueden graficar tanto los diagramas de cortante como diagramas de momento flector rápidamente en una planilla de cálculo o en Matlab. Hice un vídeo donde enseño como crear un pequeño programa en excel para la graficación automática de estas ecuaciones. VIDEO AQUÍ.

Los diagramas de cortante y momento flector son entonces:

Vídeo

El vídeo de este artículo lo tengo en youtube, y lo puedes ver a continuación

autor: Marcelo Pardo

← ← ← VOLVER A TABLA DE CONTENIDO DE ELEMENTOS FINITOS← ← ←