Enunciado
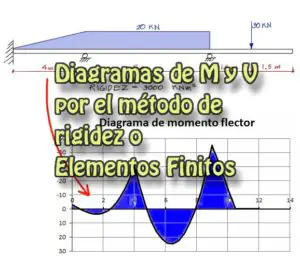
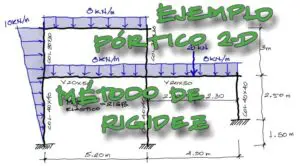
El ejercicio consiste en calcular los desplazamientos, deflexiones, solicitaciones y reacciones del pórtico siguiente:
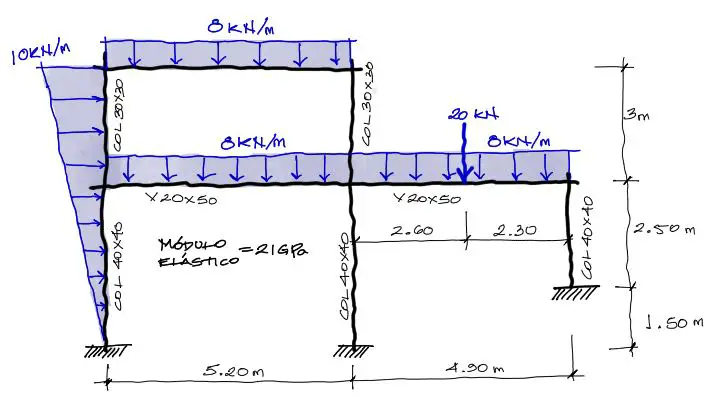
El pórtico en 2 dimensiones tiene la variedad suficiente de cargas típicas encontradas en un pórtico real. La estructura es de concreto reforzado y las secciones también estan cercanas a un caso real.
Solución
El método a aplicar será el Método de Rigidez, donde cada elemento está gobernado por una matriz de rigidez y también por una matriz de transformación de coordenadas (matriz de rotación) como se explica en el enlace Matriz de rigidez por el método de rigidez.
Numeración de nudos y barras
El primer paso siempre es la numeración de nudos y elementos. Un método que sirve para estructuras más anchas que altas, es barrer la numeración de nudos de izquierda a derecha sin dejar ningún nudo numerado. Lo mismo pasa con las barras. Entonces se tiene la siguiente numeración:
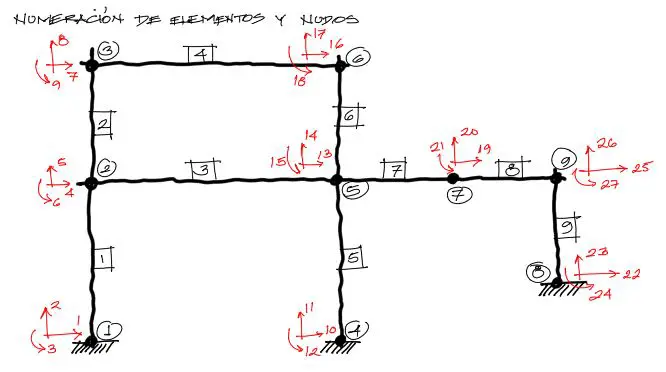
Además de la numeración de nudos, es una buena práctica numerar los grados de libertad EN EL MISMO ORDEN QUE LA NUMERACIÓN DE LOS NUDOS.
Matrices de rigidez de cada elemento.
Tanto por el método de rigidez como por el método de elementos finitos se llega a la misma matriz final (para un elemento con dos nudos y sin nudos centrales). La matriz de rigidez para cada barra es la siguiente:
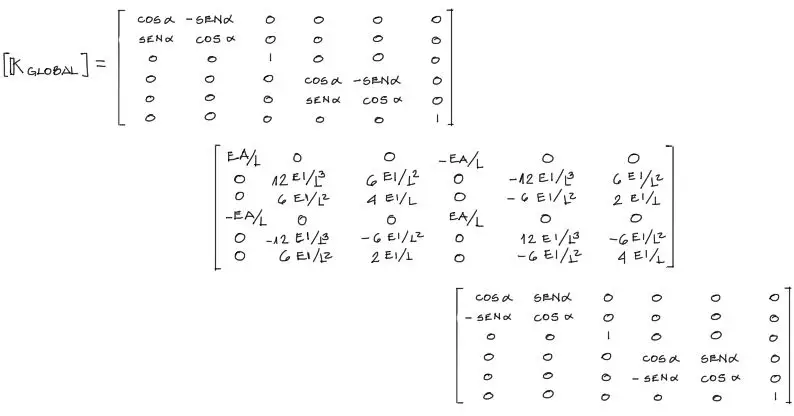
La primera y última matriz corresponden a matrices de transformación de coordenadas (más concretamente rotación de coordenadas). La matriz del centro corresponde a la matriz de rigidez propiamente dicha en coordenadas locales. El resultado de la multiplicación de las tres matrices da como resultado una matriz de rigidez del elemento estudiado pero en coordenadas globales.
Nota que entre los datos a introducir a las matrices necesitamos conocer la superficie transversal “A” y la inercia “I” de cada elemento. Estos datos los calculamos para las tres secciones transversales que se plantean en el enunciado.
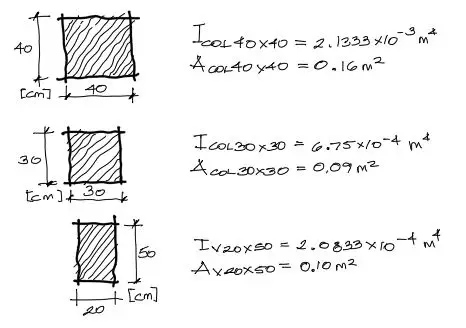
Aplicando la fórmula mostrada a los nueve elementos del pórtico, tenemos:
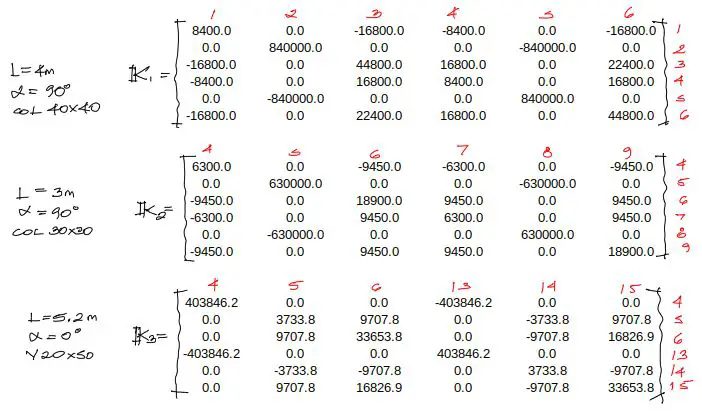

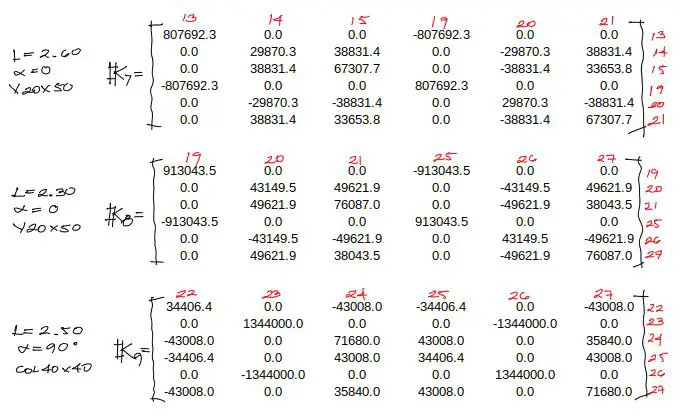
Debes notar que cada matriz de rigidez lleva encima y al lado derecho una numeración en rojo. Esta numeración es la numeración correlativa de los grados de libertad a los que está conectada cada barra, en orden X,Y,giro primero para el extremo inferior o izquierdo y luego para el extremo superior o derecho.
Ensamblaje de la matriz de rigidez
Una vez encontradas las matrices de rigidez de cada elemento es hora de posicionar cada una de estas matrices en su posición final dentro de la matriz de rigidez global.
Este es tal vez uno de los pasos donde más errores se puede cometer si es que se lo hace manualmente. Es por eso que NUNCA se debe ensamblar una matriz de rigidez a mano. Generalmente es más práctico y necesario utilizar un bucle de programación donde se ensamble cada matriz elemental automáticamente dentro de la matriz global.
Cada elemento debe trasladarse de la matriz de rigidez elemental a la posición de los números rojos a la matriz de rigidez global. Si dos valores de diferentes matrices elementales caen dentro de la misma casilla de la matriz de rigidez global, se suman los valores.
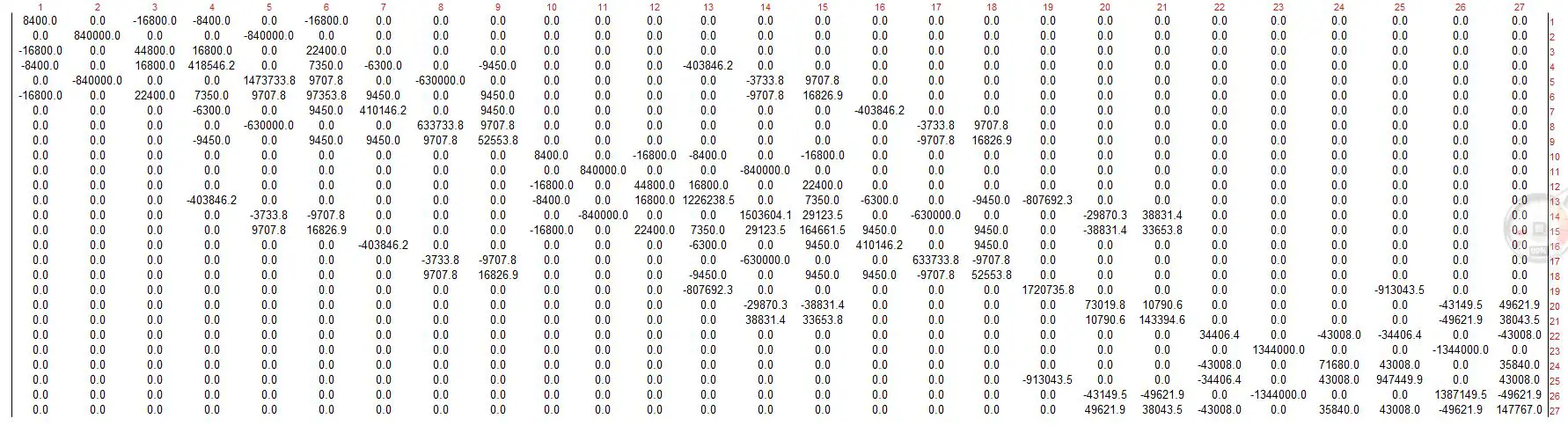
Luego del ensamblaje de la matriz de rigidez global, la matriz queda así: (Para ver la imagen en tamaño real puedes hacer click en esta última imagen)
Código de ensamblaje en Octave y video tutorial
En la publicación del enlace puedes ver un vídeo tutorial donde enseño como ensamblar las matrices de rigidez elementales a una matriz de rigidez global de manera automática en Octave o Matlab. Además puedes descargar el código.m.
ENSAMBLAJE DE MATRIZ DE RIGIDEZ DE PÓRTICOS DE ESTRUCTURAS CON OCTAVE O MATLAB
Que sigue?
Luego de tener la matriz de rigidez ensamblada se llegó a la mitad del análisis. En el siguiente artículo explico la obtención de los vectores de carga y la resolución del sistema de ecuaciones. Continúa con el ejercicio en el siguiente enlace:
autor: Marcelo Pardo

Como hariamos si tuvieramos una articulacion en este proceso sistematizado.
Daniel, se debe aplicar una matriz de rigidez especial en la barra con la articulación. por el momento solo tengo el ejemplo para elementos de viga. Sin embargo es muy similar para un pórtico
Buen día profe cómo está? Tengo una inquietud, tengo entendido que la matriz para columnas es una y para vigas es otra, y en el ejercicio se está determinando todo con la matriz de vigas ¿Me podrías clarificar al respecto por favor? Saludos desde Colombia. Excelente contenido
Diego, la matriz de rigidez para ambos tipos de elementos es la misma. solo cambia el ángulo de rotación. 90° para columnas y 0° para vigas
Buen dia profesor, le agradezco sobremanera sus explicaciones y le mando un caluroso abrazo hasta su hogar desde la parte nortel del continente. Tengo una pequeña duda, en la barra elemento 7 al obtener sus momentos de empotramiento el nodo numero 7 estaba cargado con 20KN, los cuales ya no aparecieron en el vector de fuerzas de ese elemento ni del elemento barra 8. ¿En este caso, estamos despreciando esa carga? Muchisimas gracias por sus aportes y sus geniales videos 🙂
Luis, no lo estamos pasando de largo. De hecho la carga del nudo 7 aparece en el vector de cargas puntuales al final del artículo https://marcelopardo.com/ejemplo-portico-2d-cargas-distribuidas-2da-parte/
Hola profe.. un gusto disfrutar sus videos… Podría hacer un vídeo del cálculo de la armadura de una columna ?
Muy bien Alejandro. Voy a preparar algún vídeo al respecto
Ingeniero, muchas gracias por el aporte y el método utilizado.
¿En qué parte de esta tu página puedo empezar a aprender este método para poder comprender de donde salió la matriz de rigidez y las demás matrices?
¡¡Saludos!!
Miguel, la verdad la sección de método de rigidez está aun muy incompleta. la iré completando de a pooco
Yo número los nodos de manera que intersecten todas las barras de manera continua para lograr el ancho de banda.
Muchas gracias Dani!
Busca cursos remediales FES Aragón Curso completo de análisis matricial.