Pasos previos
El enunciado del problema es el siguiente:
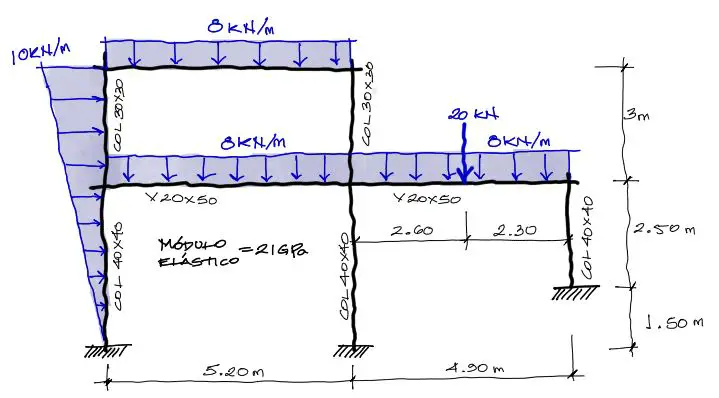
Sobre esta estructura, hemos numerado tanto nudos como barras de la siguiente manera:

Hasta el momento hemos trabajado con en la resolución de los desplazamientos de la estructura en las anteriores publicaciones. Las publicaciones previas las dejo a continuación para que las revises:
- Cálculo de la matriz de rigidez [K]
- Cálculo del vector de cargas {f} y {p}
- Solución al sistema de ecuaciones [K]{u}={f}+{p}
Postproceso
El trabajo posterior a la solución de los desplazamientos ya corresponde al postProceso de resultados. Estos consisten en:
- Encontrar los elementos deformados
- Encontrar solicitaciones
- Graficación de deformaciones y Solicitaciones
Ese es el trabajo que abordaremos en esta publicación.
Reseña teórica
En el análisis de deformaciones y solicitaciones de un elemento de pórtico, debemos separar a este elemento imaginariamente en dos. Una primera fase del elemento que se comporta con deformaciones axiales (como si fuera un elemento de cercha) y una segunda fase donde el elemento se comporta como una viga, generando solicitaciones de flexión y cortante. Este proceso está explicado en la publicación Métod de Rigidez – Diagramas axiales, de flexión y corte para pórticos.
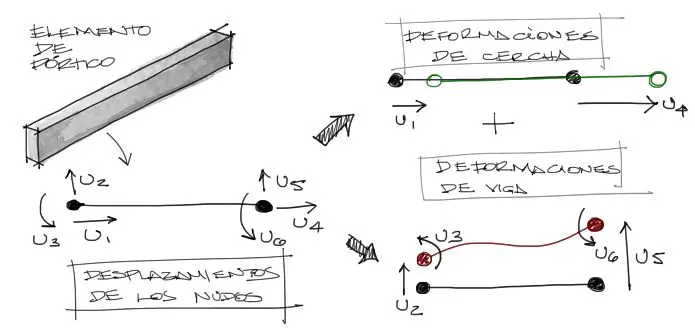
Para el trabajo en este ejemplo no trabajaremos sobre todas las barras, sino solo sobre el tramo 2 (tal cual hicimos en la Obtención de cargas equivalentes en los nudos) que será suficiente como caso general para entender como proceder en el cálculo de las solicitaciones para cada barra. El proceso es identico en cada caso.
Elemento 2
Transformación de desplazmientos globales a locales
Los desplazamientos globales en el elemento de pórtico 2 son:
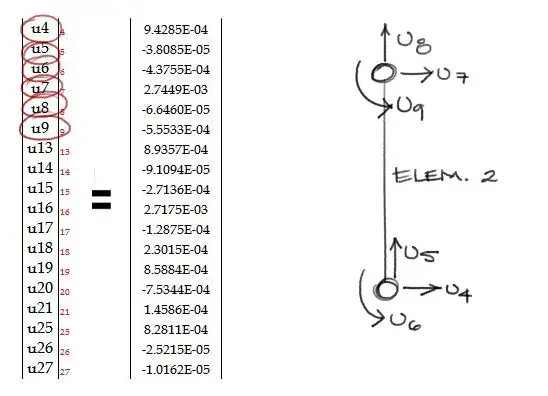
Numéricamente y con las direcciones dibujadas, los desplazamientos se ven de la siguiente manera:
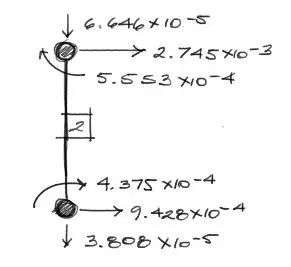
El ángulo de rotación de esta barra respecto a la posición sin rotar son 90°. Por tanto los desplazamientos locales de la barra son:
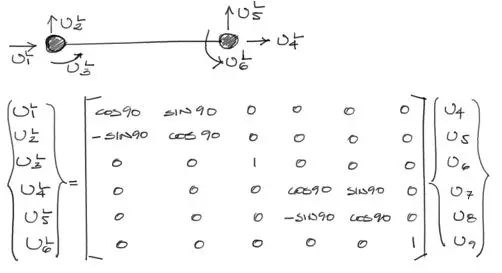
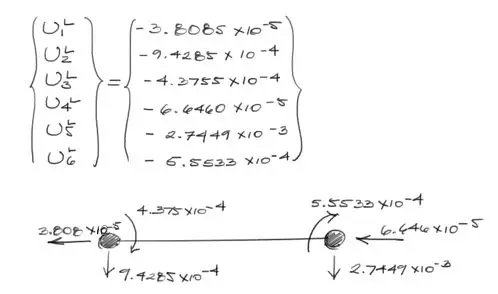
Y operando nos queda:
Solicitaciones axiales
Tenemos los desplazamientos U de toda la estructura. Si queremos a partir de estos encontrar las solicitaciones axiales de una barra, debemos aplicar la fórmula de la teoría, con los datos de rigidez A*E, longitud y desplazamientos locales u1 y u4. Se tiene entonces la fórmula:

Si reemplazamos todo en metros, y KPa, el resultado lo obtendremos en KN. En este caso negativo representa compresión. Debemos entender de la fórmula, que reemplazando con los signos los desplazamientos locales u1 y u4, obtenemos automáticamente el efecto axial positivo a tracción o negativo a compresión.
Solicitaciones de Cortante y momento flector
Para conocer las solicitaciones de momento y cortante, debemos primeramente conocer los coeficienes C1, C2, C3, C4 de la fórmula de la elástica explicada en el artículo de teoría. Para eso, necesitamos los siguientes datos de la barra:
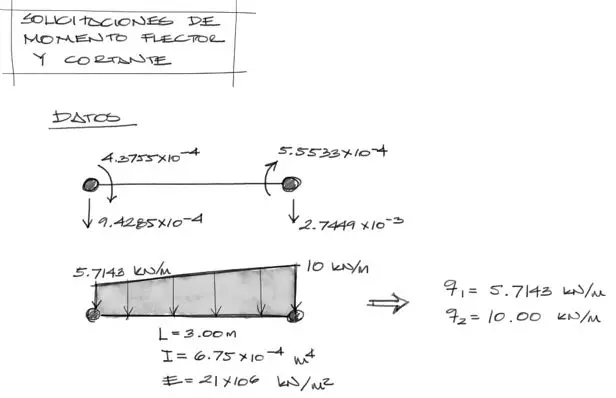
Los desplazamientos verticales locales de cada nudo y rotaciones vienen dados por los desplazamientos locales calculados antes. Las carga de 5.7143 en el extremo izquierdo de la barra es parte de la interpolación de carga distribuida explicada en la Parte 2 de este ejercicio. Luego las rigideces y longitudes las conocemos del encunciado.
Todos estos datos deben entrar en la siguiente fórmula:
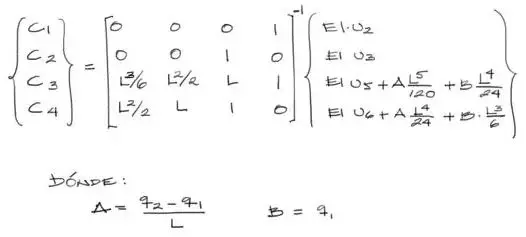
Reemplazando todos los datos en este sistema de ecuaciones, obtenemos inmediatamente las constantes de integración C1 a C4:
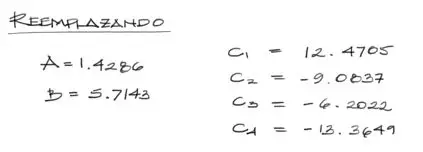
Y a partir de estas constantes, más las constantes A y B, se pueden directamente conocer las ecuaciones de momento y de cortante para este elemento de pórtico
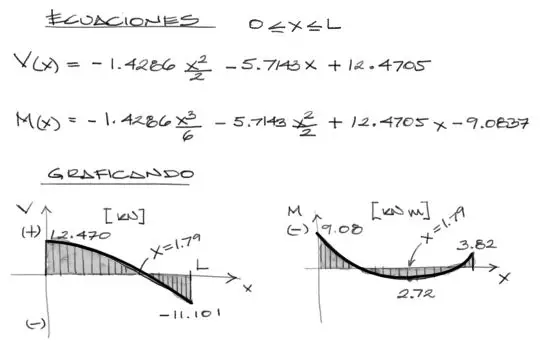
Debemos observar que el dominio en el cual trabajamos para la obtención de las ecuaciones de V y M estan en el rango de 0 a L para la variable “x”.
Cálculos
Todos los cálculos han sido desarrollados en un documento de MatLab (u octave) que puede descargarse EN ESTE ENLACE para su verificación. El archivo está comprimido en ZIP.
autor: Marcelo Pardo