Planteamiento del problema
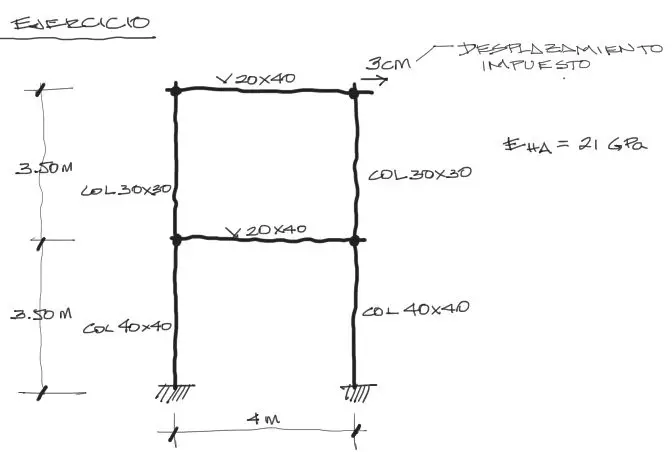
Se pretende resolver la siguiente estructura de pórtico, con columnas y vigas como las mostradas en la imagen. Se impone un desplazamiento de 3cm en la esquina superior derecha del pórtico y se pide encontrar las reacciones y solicitaciones de momento flector en dicho pórtico producto del desplazamiento. No se aplican otras cargas.
Solución de desplazamientos
Se abordará el problema por el método de rigidez, que es el método más adecuado de análisis. Primero se encontrarán los desplazamientos de todos los nudos. Posteriormente las reacciones de los apoyos y finalmente las solicitaciones de las barras.
Numeración de nudos y barras
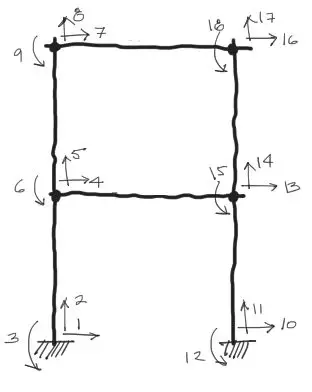
La numeración se realiza de abajo hacia arriba y de derecha a izquierda tanto para nudos como barras. Los nudos se simbolizan con círculos y las barras con etiquetas rectangulares:
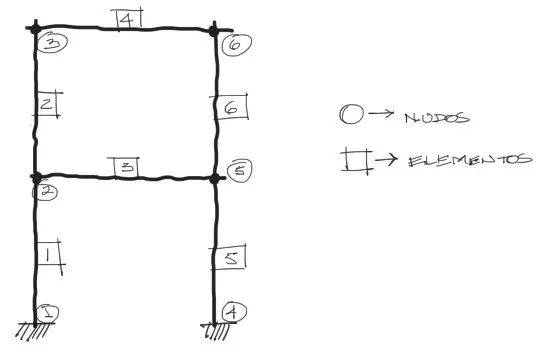
Además a partir de la numeración de los nudos mostrada, es conveniente mostrar la numeración de los grados de libertad de todos los nudos. La numeración de los GDL debe seguir el mismo orden que la numeración de nudos.
Matrices de rigidez de cada elemento
A partir de la teoría de matrices de rigidez de un elemento de pórtico podemos deducir la matriz de rigidez de cada elemento. A continuación se escriben los datos de cada barra, así como los grados de libertad de la matriz. (los 3 primeros GDL corresponden al nudo de arranque y los 3 siguientes al nudo de llegada de la barra). En todos los casos el módulo elástico es de E=21e6 [KPa]. Tomemos en cuenta que todas las unidades deben estar en [KN] y en [m]

Matriz de rigidez de toda la estructura
Se debe ensamblar la matriz de rigidez de toda la estructura a partir de las matrices de rigidez de cada elemento mostrado arriba.
Para tal propósito, debemos crear una matriz cuadrada con la dimensión igual a la cantidad de grados de libertad de la estructura (18 GDL). Luego se debe ir transportando cada una de las 6 matrices de cada elemento a la respectiva posición de la matriz de toda la estructura según los grados de libertad tanto de filas como de columnas de las matrices de cada elemento.
Luego de todo el ensamblaje, la matriz queda así (click para expandir):
Insertar el desplazamiento impuesto
La matriz de rigidez de toda la estructura recién encontrada, forma parte de un sistema de ecuaciones [K]{u} = {F} donde: [K]: Matriz de rigidez de toda la estructura
{u}: Vector columna con los desplazamientos de cada grado de libertad (desde u1 hasta u18)
{F}: Vector columna con las Fuerzas aplicadas a la estructura
Se conoce que el desplazamiento horizontal en la esquina superior derecha corresponde al GDL 16, por tanto u16 = 0.03 [m]. Se supone que la matriz de rigidez multiplica a los desplazamientos y que en la multiplicación de las columnas de [K] por todas las componentes de {u}, la componente u16 = 0.03 multiplica todos los elementos de la columna 16 de la matriz de rigidez.
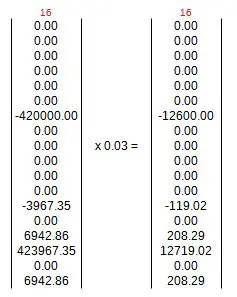
Este vector obtenido de tal multiplicación ya puede formar parte de los términos independientes del sistema de ecuaciones, o dicho de otra manera, formará parte de los vectores de carga a la derecha del sistema.
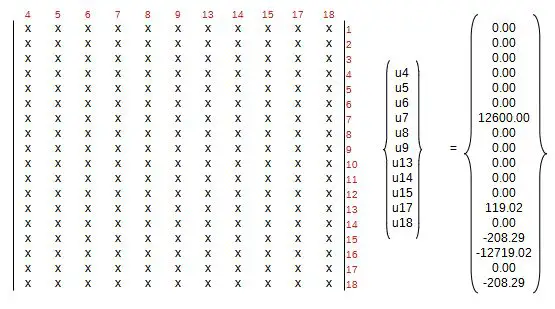
De la misma manera los desplazamientos de los GDL 1, 2, 3, 10, 11, 12 corresponden a los apoyos, cuyos desplazamientos u1, u2, u3, u10, u11, u12 son nulos y por tanto multiplicando a las columnas 1, 2, 3, 10, 11, 12 de la matriz [K], las anulan, quedanto entonces:

Solución de los desplazamientos
De este sistema de ecuaciones, eliminamos las filas 1, 2, 3, 10, 11, 12 y 16, que corresponden a los grados de libertad cuyos desplazamientos se conocen, quedando un sistema de 11 ecuaciones con 11 incógnitas que son los desplazamientos y que ya pueden resolverse por cualquier método, como Gauss Jordan.
Despejando entonces el vector de desplazamientos {u} se tiene:
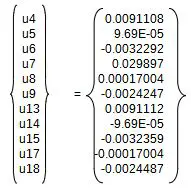
Se puede completar este vector de desplazamientos, con los desplazamientos faltantes conocidos,quedando:

Reacciones
Las reacciones podemos encontrarlas reemplazando estos desplazamientos ya conocidos dentro del sistema de ecuaciones original, notando que en los grados de libertad donde existen restricciones de apoyo, en el extremo derecho del sistema aparecen Reacciones Ri, que son las nuevas incógnitas a resolver.
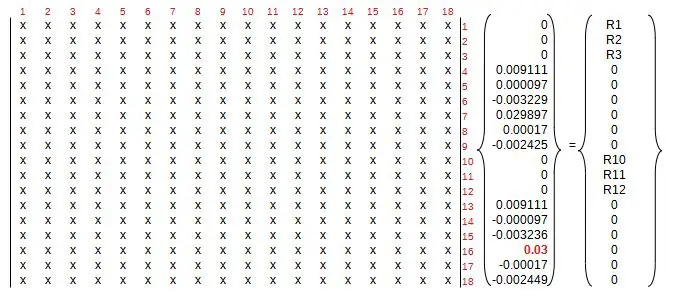
Multiplicando entonces [K]*{u} e igualando con el vector de reacciones derecho, se tiene:

Gráfica de los desplazamientos y reacciones
Magnificando en escala los desplazamientos y dibujando las reacciones, bajo la convención de signos: positivo vector derecho, positivo vector arriba, y positivo giro antihorario, se tiene:
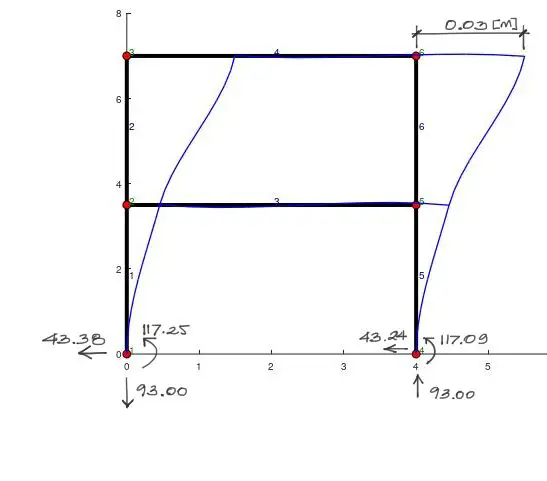
Post-Proceso (Solicitaciones)
Se realizará el análisis y obtención de las solicitaciones de momento flector para un solo elemento en el entendido de que la obtención de las solicitaciones para todos los otros elementos del pórtico es similar.
En esta publicación analizaremos el elemento 6.
Desplazamientos en coordenadas locales
Se tienen los desplazamientos de todos los nudos de la estructura en coordenadas globales. Por ejemplo, si analizamos dibujamos el elemento 6 junto con los desplazamientos de sus nudos (ya deducidos arriba) se tiene:
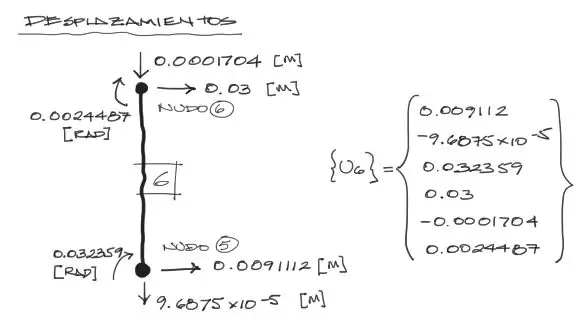
Estos desplazamientos debemos transformarlos a desplazamientos locales cuando la barra no está rotada (Este elemento en particular tiene una rotación de 90° antihoraria). Para lograr esto debemos multiplicar los desplazamientos en coordenadas globales de esta barra, por la matriz de transformación [T], de la siguiente manera:
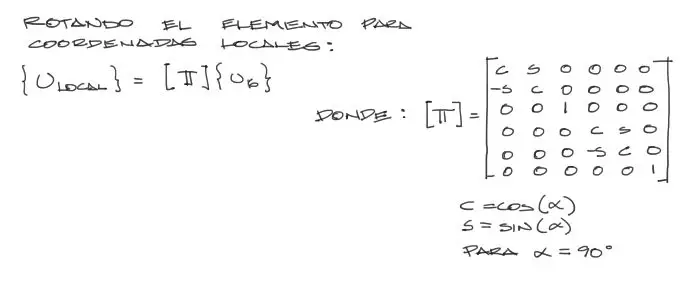
Realizando estas operaciones, obtenemos los desplazamientos locales siguientes para la misma barra, pero orientada horizontalmente.
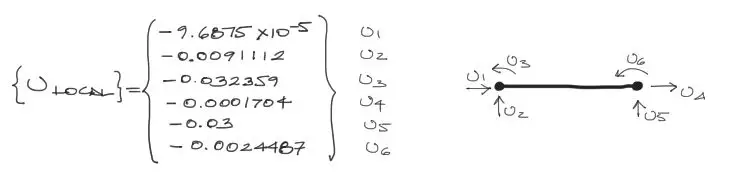
De esta manera, los desplazamientos 1 y 4 corresponden a las deformaciones axiales. Los desplazamientos 2 y 5 junto con los giros 3 y 6 producen el efecto combinado de cortante y flexión en el elemento.
Solicitaciones axiales
Como se mencionó, las solicitaciones axiales se encuentran a partir de los desplazamientos u1 y u4 locales de la barra en análisis. En este caso, a partir de resistencia de materiales:

Solicitaciones de flexión
La teoría de la deducción de momentos flectores y cortantes es un tanto larga. Puedes revisarla en el enlace MOMENTOS FLECTORES A PARTIR DE DESPLAZAMIENTOS EN LOS EXTREMOS. Acá solo usaremos la fórmula final del sistema de ecuaciones lineales necesario ya resuelto:

Con los datos de la barra mostrados abajo del sistema de ecuaciones en forma matricial, se realiza el reemplazo de todos los términos. A y B son nudos puesto que en esta barra no existen cargas distribuidas para este ejercicio.
Resolviendo el sistema, obtenemos las cuatro constantes de integración C1 a C4.

Estas constantes de integración forman parte de la ecuación genérica de los diagramas de cortante, momento flector, pendiente de deflexión y deflexión:
- Cortante V(x) = -Ax^2/2 – Bx + C1
- Momento Flector M(x) = -Ax^3/6 – Bx^2/2 + C1x + C2
Reemplazando A, B, C1 y C2 en la ecuación genérica de momento, y graficando, obtenemos:
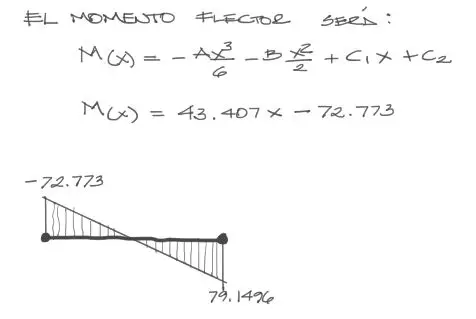
Recordarás que la barra originalmente se encuentra en sentido vertical, por tanto rotando tanto solicitaciones como la barra misma, tenemos:
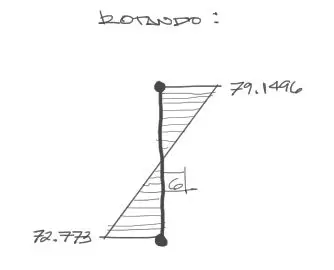
Solicitaciones finales
Se repite el procedimiento anterior para todas las barras del pórtico, y así obtenemos el siguiente resultado:
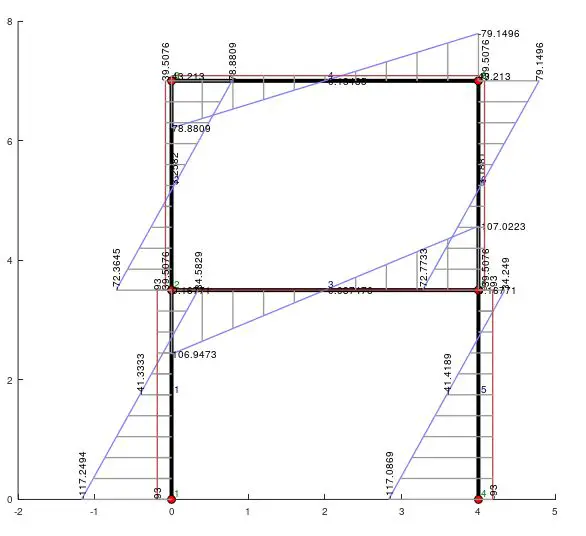
Se puede hacer lo mismo con las ecuaciones de cortante, pendiente de deflexión y deflexión. Queda con esto terminado el proceso de resolución del pórtico con desplazamientos impuestos.
autor: Marcelo Pardo